biharmonic专题
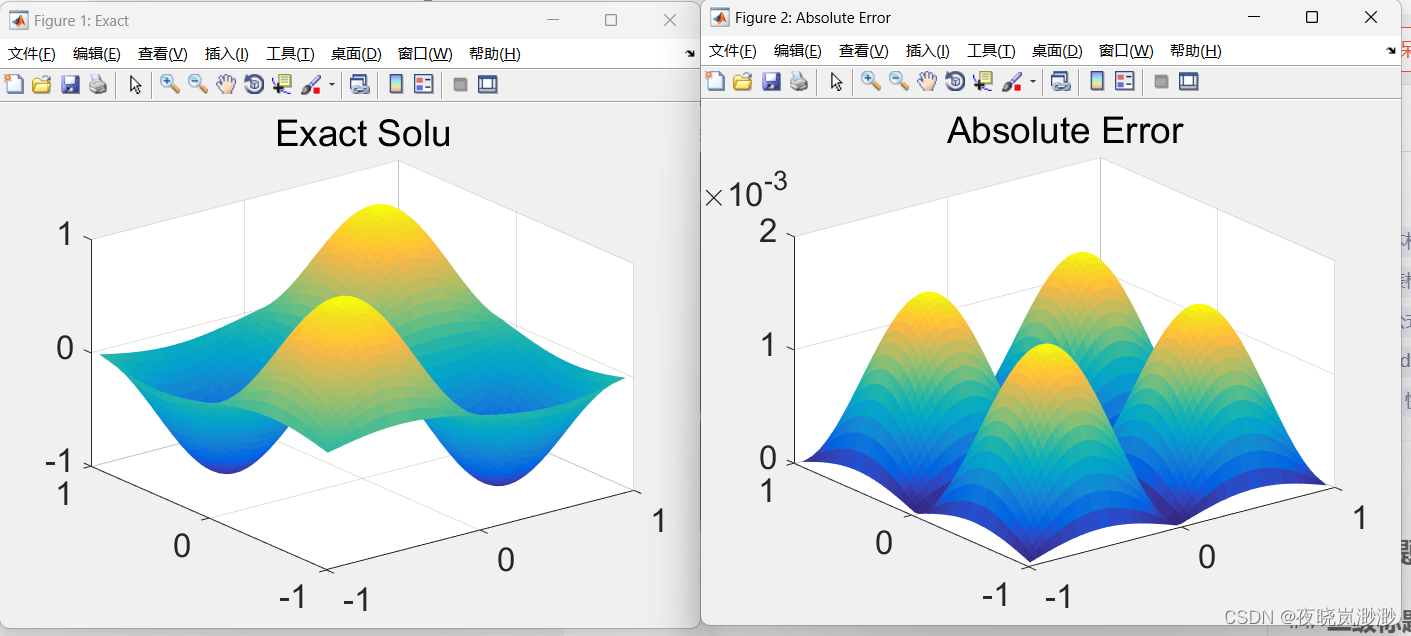
matlab:五点中心差分求解Navier边界的Biharmonic方程(具有纳维尔边界的双调和方程)
我们考虑如下形式的双调和方程的数值解 其中,Ω是欧氏空间中的多边形或多面体域,在其中,d为维度,具有分段利普希茨边界,满足内部锥条件,f(x) ∈ L2(Ω)是给定的函数,∆是标准的拉普拉斯算子。算子∆u(x)和∆2u(x)表示为 巧妙地将双调和方程(1.1)分解为两个Possion方程,传统的数值方法如有限元法(FEM)和有限差分法(FDM)在计算资源和时间复杂度较小的情况下表现良好。通过
Bounded Biharmonic Weigths for Real-Time Deformation
3.1 Formulation { First of all, let me explain the physical meaning of the objective function. The function tries to make the weight of each anchor point on each point have least changed. The ide
Bounded Biharmonic Weigths for Real-Time Deformation
3.1 Formulation { First of all, let me explain the physical meaning of the objective function. The function tries to make the weight of each anchor point on each point have least changed. The ide