左神算法笔记（十八）——平衡搜索二叉树

搜索二叉树

搜索二叉树：对于搜索二叉树的任何一个节点，左子树的值都比节点小，右子树的值都比他大。
TreeMap中，跟HashMap中一样可以提供key-value，同时会将key按照大小顺序排列。中间采用的就是搜索二叉树的知识。

具备平衡性的搜索二叉树：

AVL树——平衡性最严格

任何一个节点的左子树和右子树高度差不大于1，复杂度还是O(logN)。导致调整非常频繁。

红黑树——平衡性要求不严格

每个节点染上色，头和叶节点必然黑，相邻两个节点不能出现连续的红节点，任何一条链，黑色节点个数相差不超过1.所以任何一条链的最长链和最短链的高度差不超过1倍。

搜索二叉树代码

需要具备增删改查的功能，此时没有考虑平衡性

public class BinarySearchTree{	//根节点public Node root;//树的大小protected int size;//二叉树查找的功能public Node search(int element){Node node = root;//如果最后找到了就返回node，如果node不存在为null，也返回nodewhile(node != null && node.value != null && node.value != element){if(element < node.value){node = node.left}else{node = node.right;}}return node;}//插入，增加功能public Node insert(int element){if(root == null){root = createNode(element,null,null,null);size++;return root;}Node insertParentNode = null;Node searchTempNode = root;//insertParentNode在一直往下走，直到走到叶节点为止while(searchTempNode != null && searchTEmpNode.value != null){insertParentNode = searchTempNode;if(element < searchTempNode.value){searchTempNode = searchTempNode.left;}else{searchTempNode = searchTempNode.right;}}//将要插入的值和当前的节点进行比较，小于当前的节点，则放到当前节点的左边，否则放到当前节点的右边。Node newNode = createNode(element,insertParentNode,null,null);if(insertParentNode.value > newNode.value){insertParentNode.left = newNode;}else{insertParentNode.right = newNode;}size++;return newNode;}//删除功能/** 删除功能比较麻烦，如果删除节点只存在左子树，则删除该节点左子节点直接顶替位置就可以，同理，如果只存在右子树，则将右子节点直接顶替位置。如果此时删除的节点是左右子树都有，则此时将右子树的最左节点顶到删除节点，如果右子树的最左节点此时存在右子树，则将右子树移交给自己的父节点 */public 	Node delete(int element){Node deleteNode = search(element);if(deleteNode != null){return delete(deleteNode);}else{return null;}}protected Node delete(Node deleteNode){if(deleteNode != null){Node nodeToReturn = null;if(deleteNode != null){if(deleteNode.left ==null){nodeToReturn = transplant(deleteNode,deleteNode.right);}else if(deleteNode.right == null){nodeToReturn = transplant(deleteNode,deleteNode.left);}else{Node successorNode = getMinimum(deleteNode.right);if(successorNode.parent != deleteNode){transplant(successorNode,successorNode.right);successorNode.right = deleteNode.right;successorNode.right.parent = successorNode;}transplant(deleteNode,successorNode);successorNode.left = deleteNode.left;successorNode.left.parent = successorNode;nodeToReturn = successorNode;}size--;}return nodeToReturn;}return null;}//将节点从一个位置挪到另外一个位置private Node transplant(Node nodeToReplace,Node newNode){if(nodeToReplace.parent == null){this.root = newNode;}else if(nodeToReplace == nodeToReplace.parent.left){nodeToReplace.parent.right = newNode;}if(newNode != null){newNode.parent = nodeToReplace.parent;}return newNode;}.....

搜索二叉树添加平衡性

对于搜索二叉树中的平衡性，都是针对二叉树进行左旋或右旋的调整，不同的搜索二叉树只是针对于左旋和右旋的动作组合。将整个搜索二叉树进行高度的调整，使其实现平衡性。

AVL发现不平衡的机制：
当二叉树进行删除和添加的时候，可能导致二叉树不平衡。
添加或删除时：对于整个二叉树而言存在添加数的时候除了添加节点信息以外，还需要添加左子树和右子树的最大高度信息，当插入一个值的时候，如果树的某一子树高度发生改变，则此时会对父节点存储的最大高度的信息进行更新，会 一直更新到跟节点，然后依次判断高度是否一致或最多相差1，如果不满足，则此时发生左旋或右旋的操作，使其实现平衡。
调整组合类型：LL，RR，LR，RL
LL（左边的左边较长）：此时简单进行一个向右就可以
RR（右边的右边较长）：此时简单进行一个左旋就可以
RL（右边的左边较长）：首先将右边的左边节点变成父节点，然后进行右旋
LR（左边的右边较长）：首先将左边的右边节点变成父节点，然后再进行左旋

AVL树调整平衡性代码

AVL树继承了原本的node类型，但是增加了一个height。

public void rebalance(AVLNode node){while(node != null){Node parent = node.parent;int leftHeight = (node.left == null)? -1:((AVLNode) node.left).height;int rightHeight = (node.right == null) ? -1 : ((AVLNode)node.right).height;int nodeBalance = rightHeight -leftHeight;if(nodeBalance == 2){if(node.right.right != null){node = (AVLNode)avlRotateLeft(node);break;}else{node = (AVLNode)doubleRotateRightLeft(node);break;}//此时为左树超了}else if(nodeBalance == -2){此判断是LL型if(node.left.left != null){//此时只进行一个右旋的操作node = (AVLNode)avlRotateRight(node);break;}else{node = (AVLNode)doubleRotateLeftRight(node);break;}}else{updateHeight(node);}node = (AVLNode)parent;}
}
//确立这棵树的高度，从node开始就从本节点开始依次向上调整看是否平衡，
private static final void updateHeight(AVLNode node){int leftHeight = (node.left == null) ? -1:((AVLNode) node.left).height;int rightHeight = (node.right == null) ? -1:((AVLNode) node.right).height;node.height = 1+ Math.max(leftHeight,rightHeight);
}

红黑树的应用

1. 使用过程包含哈希表的内容，可以使用treeMap.containsKey(i)来返回是否包含key为5。同样也可以treeMap.get（i)来拿出i所对应的value。
2. 有比哈希表中更加方便的获取内容：treeMap.lastKey（），获取最大的key，获取的过程只需要一路向右的节点，复杂度为O(logN)，treeMap.ceilingKey(k)，来找出在整个二叉树中跟k相等的数，如果没有则找到比k大的最小值。treeMap.floorKey(k)就是寻找小于等于k的最大值。这里面的所有用法都比传统的哈希表快上很多倍。

例题一

思路：

1. 将每一个矩阵进行拆分，第一个【1，3，3】拆分为（1，3，上）和（3，3，下），第三个拆分成（5，1，上）和（6，1，下）
2. 将位置按照从小到大进行排序，轮廓的变化意味着较低的高度被较高的高度进行覆盖，覆盖住之后此时出现轮廓。
3. 建立一张treeMap，将大楼信息拆分成两个，一方面是位置，高度，增加，另一个是位置，高度，减少。此时在map中保存key为某一个高度的高度线，value为某一个高度有几条。
4. 在遍历整个矩阵过程中，在treeMap中新建节点，此时可以知道最大高度是否发生变化，从而确定当前位置是否产生轮廓。只要上就增加，下就减少，所以，当过了一个矩阵的时候，此时次数信息为0，此时将对应节点删除。

代码

//Node格式与内容
public static class Node{public boolean be;public int p;public int h;public Node(boolean boRe,int position,int height){be = bORe;p = position;h = height;}
}public static class NodeComparator implements Comparator<Node> {@Overridepublic int compare(Node o1,Node o2){if(o1.p != o2.p){return o1.p-o2.p;}if(o1.be != o2.be){return o1.be ? -1:1;}return 0;}
}public static List<List<Integer>> buildingOutline(int[][] buildings){Node[] nodes = new Node[buildings.length *2];for(int i =0;i<buildings.length;i++){//在放置的时候，将向上的信息和向下的信息收集nodes[i *2] = new Node(true,buildings[i][0],building[i][2]);nodes[i*2+1] = new Node(false,buildings[i][1],buildings[i][2]);}//按照严格的位置排序Arrays.sort(nodes,new NodeComparator());//htMap进行标记最大高度信息，pmMap记录每一个位置冲到的最大高度//key为高度信息，value是出现次数TreeMap<Integer,Integer> htMap = new TreeMap<>();//key是位置，遍历pmMap时，会严格按照key升序TreeMap<Integer,Integer> pmMap = new TreeMap<>();for(int i = 0;i<nodes.length;i++){//进行向上还是向下的判断if(nodes[i].be){//如果高度第一次出现，则将当前节点放入if(!htMap.containsKey(nodes[i].h)){htMap.put(nodes[i].h,1);}else{//如果之前出现过，则此时将出现次数+1htMap.put(nodes[i].h,htMap.get(nodes[i].h)+1);}}else{//此时是向下的情况if(htMap.containsKey(nodes[i].h)){//如果现在的高度是1，再减去1，所以需要将现在的节点移除if(htMap.get(nodes[i].h) == 1){htMap.remove(nodes[i].h);}else{//高度大于1，则此时将高度减一htMap.put(nodes[i].h,htMap.get(nodes[i].h)-1);}}}if(htMap.isEmpty()){pmMap.put(nodes[i].p,0);}else{pmMap.put(nodes[i].p,htMap.lastKey());}}List<List<Integer>> res = new ArrayList<>();int start = 0;int height = 0;//因为为treeMap，所以拿出当前位置时是升序排列的for(Entry<Integer,Integer> entry : pmMap.entrySet()){int curPosition = entry.getKey();int curMaxHeight = entry.getValue();//如果之前的高度跟新拿出的高度不同，则意味着此时要生成轮廓线if(height != curMaxHeight){//如果之前的高度为0，则意味着此时开启新的轮廓线，此时跳过if，直接设置起始位置和height//高度不同，也不为0，则也会设置起始位置和heightif(height != 0){//形成整个轮廓线List<Integer> newRecord = new ArrayList<Integer>();newRecord.add(start);newRecord.add(curPosition);newRecord.add(height);res.add(newRecord);}start = curPosition;height = curMaxheight;}}return res;
}

例题二

给定一个数组arr，数组中有0，正值和负值，给定一个aim值，求累加和为给定值的最长子数组。
一旦出现连续的子数组，子串之类的题，一旦求出必须以每个位置数截止的最长子数组，最长的子数组必定在其中

思路

使用sum表示从0开始累加到当前位置的所有数目的和，在以当前位置结尾时，此时计算从0开始累加到哪个位置最早出现sum-aim，则此时的数组为以当前位置结尾的最长子数组，然后当前位置++，再次计算。

个人想法：如果不考虑空间复杂度，直接设立一个新数组arr1，此时新数组中存放的是将原本数组的从0位置求和之后的数值，此时此时计算sum-aim的数值在之前的数组中是否出现过。

左神算法：设立一个map，此时map中存放的是每个数值最早出现的位置，0这个累加和出现在-1位置，之后将累加和第一次出现的值和所对应的位置存放到map中，其他跟我的想法相同。

代码

public static int maxLength(int[] arr,int aim){if(arr == null || arr.length == 0){return 0;}HashMap<Integer,Integer> map = new HashMap<Integer,Integer>();map.put(0,-1);int len = 0;int sum = 0;for(int i = 0;i< arr.length; i++){sum += arr[i];if(map.containsKey(sum-aim)){len = Math.max(i-map.get(sum-aim),len);}if(!map.containsKey(sum)){map.put(sum,i);}}return len;
}

例题三

给定一个数组，求数组中奇数和偶数数目相等的最长子数组

将奇数变成1，偶数变成-1，使得aim等于0，由题二就得到了相应的结果。

例题四

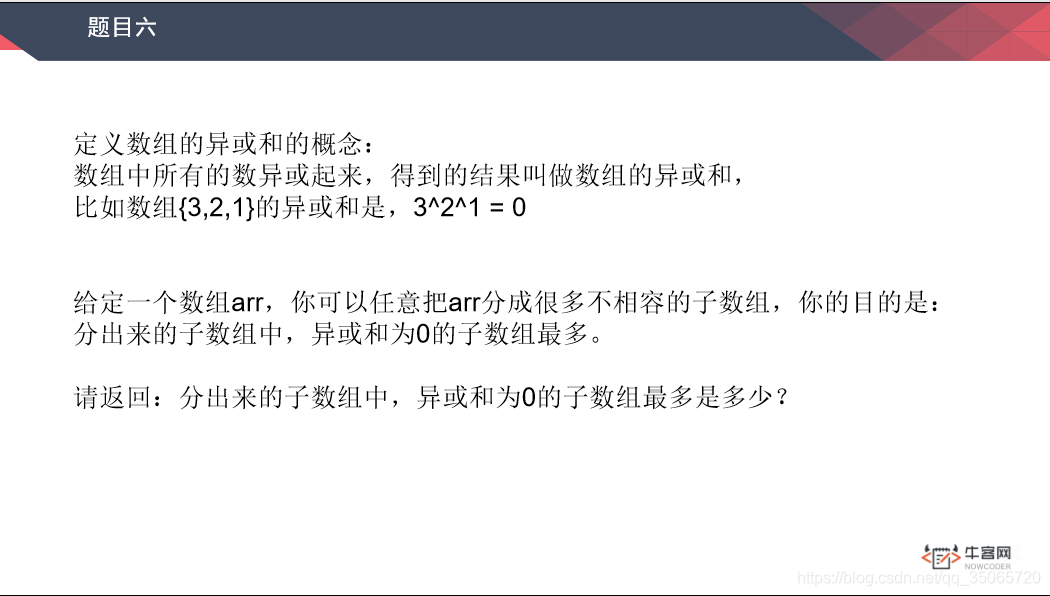
思路

求0-i的范围上最多可以求出几个异或和为0的最多子数组，然后下次求0-i+1。
假设存在最优划分，则：
若此时i不在最优划分时的划分子数组中，则此时0-i范围的最多子数组数目和跟0-(i-1)上的数目相同。
若此时i在的位置是异或和为0的子数组中，最后一个子数组中是从k开始的，则意味着k的位置一定是距离i最近的异或和为0的位置。此时的最优数组为上一个位置上的最优化分数组加一。所以这个题目转化成去求k位置，k到当前位置前一个位置最优数目都一样，此时题目转化成在整个数组中去求跟当前位置异或和为0的最晚的位置。

代码

public static int mostEOR(int[] arr){int ans = 0;int xor = 0;int[] mosts = new int[arr.length];HashMap<Integer,Integer> map = new HashMap<>();map.put(0,-1);for(int i = 0;i<arr.length;i++){xor ^= arr[i];if(map.containsKey(xor)){int pre = map.get(xor);most[i] = pre == -1 ? 1: (mosts[pre] +1);}if(i >0){mosts[i] = Math.max(mosts[i-1],mosts[i]);}map.put(xor,i);ans = Math.max(ans,mosts[i]);}return ans；
}