本文主要是介绍『最小生成树』Kruskal算法——加边法 (并查集优化 + C++语言编写 + 例题),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
『算法原理』
在一个连通网的所有生成树中,各边的代价之和最小的那颗生成树称为该连通网的最小代价生成树(Minimum Cost Spanning Tree),简称最小生成树(MST)。
Kruskal算法之所以叫加边法,就是因为其本质是一个边一个边地加入到最小生成树中。
算法步骤如下:
设有一无向连通图G,有n个顶点。
- a.将所有边的权值从小到大排列。
- b.遍历所有的边,如果边加入生成树后不形成环,则将该边加入到生成树中
- c.重复b步骤直至所有顶点都被加入到生成树中,即生成树中加入了n-1条边
下面用图示来解释这个过程。
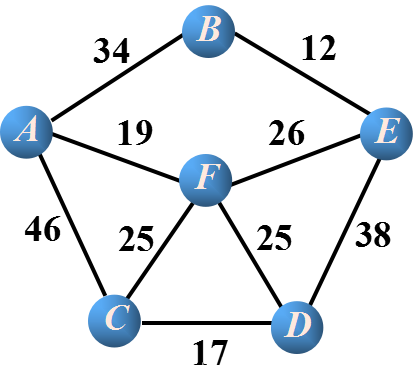
a.将所有的边从小到大排序
12 19 25 25 26 34 38 46
b.遍历所有的边,如果边加入生成树后不形成环,则将该边加入到生成树中

1).加入权最小的(B,E)
2).加入(C,D)
3).加入(A,F)
3).加入(C,F)
4).加入(F,D),此时发现 F C D形成一个环,不选
5).加入(F,E) 6个点,到此加入了5条边,生成最小生成树 算法结束
在模拟之后,大家就可以发现,Kruskal算法在代码实现时的最大困难在于“如何判断是否成环”。
模拟的过程中可以发现,n个顶点在初始状态下可看成n个独立的连通块,在不断加边的过程中,边的两端点会连在一起,形成一个连通块,故边的端点在边加入前会出现两种状态
(Vi,Vj为边的两端点)
a.Vi,Vj都属于同一连通块 例:上图中,当要加入&#
这篇关于『最小生成树』Kruskal算法——加边法 (并查集优化 + C++语言编写 + 例题)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






