第五章《数据降维:深入理解 PCA 的来龙去脉》笔记

本文主要是介绍第五章《数据降维:深入理解 PCA 的来龙去脉》笔记，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

主成分分析(Principal Component Analysis，PCA) 就是机器学习中一种常用且有效的数据降维方法。

5.1 PCA是什么

PCA 将相关性高的变量转变为较少的独立新变量，实现用较少的综合指标分别代表存在于各个变量中的各类信息，既减少高维数据的变量维度，又尽量降低原变量数据包含信息的损失程度，是一种典型的数据降维方法。PCA 保留了高维数据最重要的一部分特征，去除了数据集中的噪声和不重要特征，这种方法在承受一定范围内的信息损失的情况下节省了大量时间和资源，是一种应用广泛的数据预处理方法。

5.2 用一个例子来理解PCA过程

经过零均值化的数据预处理后，我们就可以正式开启 PCA 过程了，步骤如下。

(1)计算协方差矩阵。

(2)计算特征值与特征向量。

(3)矩阵相乘实现降维。

从上述 PCA 降维的实际过程来看，对某个矩阵 A(m×n)降维实际上就是寻找对应的降维矩阵 P(k×m)。

5.3 如何寻找降维矩阵P

5.4 PCA降维的核心思想

5.4.1 核心思想一:基变换向量投影

要实现原始数据降维就是要将矩阵 A 中每个列向量的维度或者行数合理地降低。要实现高维向量降维，一个常见的方法就是高维向量向低维空间投影。

向量 a 与向量 b 的内积结果就等于向量 a 在向量 b 方向上的投影长度 |a|cosθ。这就是向量内积的几何定义。

矩阵相乘的几何意义就是，两个矩阵相乘的结果是将右边矩阵中的每一个列向量变换到以左边矩阵中每一个行向量为基底所表示的空间中。

5.4.2 核心思想二:协方差归零投影

既然数据降维的起因是高维数据的维度之间存在较高的相关性导致数据信息存在冗余，那么数据降维的一个核心思想自然就是，数据降维后的维度之间尽可能相对独立，也就是降维之后的数据维度之间的协方差为 0。

(1)什么是方差。

方差和标准差是最常用的度量一组数据分散程度的指标。对于一组含有 n 个样本的集合，我们容易知道以下公式。

(2)协方差。

协方差度量的是维度和维度之间的关系。假设两组数据分别是 x 和 y，那么这两组数据的协方差为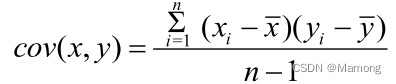

(3)协方差矩阵。

多维数据就需要多次计算协方差，也就是将多维数据中的维度数据两两计算协方差。协方差矩阵就是度量维度和维度之间关系的矩阵。

所以，我们降维之后希望各个维度之间相互独立，也就是希望降维之后不同维度之间的协方差为 0，同样也就是希望上面的协方差矩阵除了主对角线之外的部分都为 0。

5.4.3 核心思想三:最大方差投影

这种投影数据点的分散实际上就是要求原始数据矩阵降维处理之后的新矩阵的维度的方差尽可能大，也就是降维之后矩阵的协方差矩阵的对角线元素尽可能大。我们可以将这种降维投影的要求称为“最大方差投影”。

5.4.4 PCA降维的关键:协方差矩阵对角化

降维之后新矩阵 Y 的协方差矩阵 Cy 的非主对角线元素尽可能为 0，而主对角线元素尽可能大。满足上述要求的矩阵是一个对角矩阵，所以降维的实质就是要求降维之后的新矩阵 Y 的协方差矩阵 Cy 是对角矩阵。

5.5 面向零基础读者详解PCA降维

5.5.1 计算矩阵Y的协方差矩阵Cy

1.为什么计算协方差矩阵

这是因为矩阵 Y 的协方差矩阵 Cy 的主对角线元素是降维后新维度的方差，非主对角线元素是降维后各新维度的协方差。而 PCA 降维的核心思想就是“协方差归零投影”和“最大方差投影”，也就是希望降维之后得到的新矩阵 Y 的各维度间的协方差尽量为 0，而维度的方差尽可能大。上述要求翻译成数学语言，就是要求降维后矩阵 Y 的协方差矩阵为对角矩阵，这就是我们考虑计算矩阵 Y 的协方差矩阵的原因。

2.详解协方差矩阵的表达式

协方差矩阵数学表达式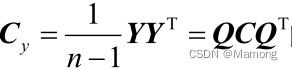的推导过程。

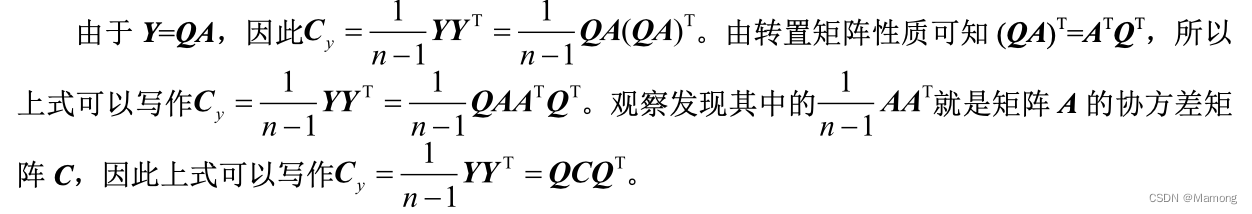
5.5.2 矩阵Y的协方差矩阵Cy对角化

1.什么样的矩阵 Q 能够对角化 Cy
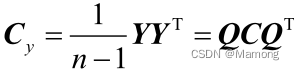根据实对称矩阵正交对角化的定理可以得到。所以，要使矩阵 Y 的协方差矩阵是对角矩阵，只需要即可。这个结果表明，矩阵 Q 如果是由原矩阵 A 的协方差矩阵 C 的特征向量构成的矩阵，矩阵 A 经过矩阵 Q 线性变换之后的矩阵 Y 的协方差矩阵 Cy 就为对角矩阵。