【SSL 1529】裴波拉契数列IIII【矩阵乘法】

本文主要是介绍【SSL 1529】裴波拉契数列IIII【矩阵乘法】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Time Limit:1000MS Memory Limit:65536K
Total Submit:53 Accepted:41

Description

求数列 $f [n] = f [n - 2] + f [n - 1] + n + 1$ 的第Ｎ项,其中 $f [1] = 1, f [2] : = 1$ .

Input

$N(１＜Ｎ＜2^31-1)$

Output

第n项结果 $m o d$ $9973$

Sample Input

10000

Sample Output

4399

Source

elba

解题思路

矩阵乘法

仿照前例，考虑 $1 \times 4$ 的矩阵 $【 f [n - 2], f [n - 1], n, 1 】$ ，希望求得某4×4的矩阵A，使得此1×4的矩阵乘以A得到矩阵：
$【 f [n - 1], f [n], n + 1, 1 】＝【 f [n - 1], f [n - 1] + f [n - 2] + n + 1, n + 1, 1 】$
容易构造出这个 $4 \times 4$ 的矩阵A，即：
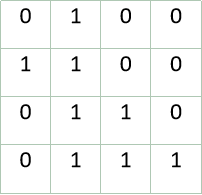
在这里插入图片描述

代码

#include<algorithm>
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
const int INF=9973;
long long n;
using namespace std;
struct c{int n,m;int a[10][10];
}A,B,CC;
c operator *(c A,c B){c C;C.n=A.n,C.m=B.m;for(int i=1;i<=C.n;i++)for(int j=1;j<=C.m;j++)C.a[i][j]=0;for(int k=1;k<=A.m;k++){for(int i=1;i<=C.n;i++)for(int j=1;j<=C.m;j++)C.a[i][j]=(C.a[i][j]+(A.a[i][k]*B.a[k][j])%INF)%INF;}	return C;
}
void poww(long long x){if(x==1){B=A;return; }poww(x>>1);B=B*B;if(x&1)B=B*A;}
int main(){scanf("%lld",&n);if(n==1){printf("1");return 0;}A.n=4,A.m=4;A.a[1][1]=0,A.a[1][2]=1,A.a[1][3]=0,A.a[1][4]=0;A.a[2][1]=1,A.a[2][2]=1,A.a[2][3]=0,A.a[2][4]=0;A.a[3][1]=0,A.a[3][2]=1,A.a[3][3]=1,A.a[3][4]=0;A.a[4][1]=0,A.a[4][2]=1,A.a[4][3]=1,A.a[4][4]=1;poww(n-1);CC.n=1,CC.m=4;CC.a[1][1]=1,CC.a[1][2]=1,CC.a[1][3]=3,CC.a[1][4]=1;CC=CC*B;printf("%d\n",CC.a[1][1]);}