本文主要是介绍论文笔记|百度AI制药大赛冠军背后的技术(ViSNet),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在首届全球AI药物研发大赛中,微软研究院王童研究员带领的ViSNet-Drug团队,凭借其团队自主开发的AI2BMD高精度动力学模拟系统、ViSNet三维分子结构建模图神经网络和蛋白质全构象数据集AIMD-Chig在三轮比赛中均排名第一并获得总冠军。王童研究员团队提出全新的新冠小分子药物解决方案:通过AI2BMD高精度的分子动力学模拟有效区分正负样本小分子与主蛋白酶靶点之间的结合自由能,利用AIMD-Chig蛋白全构象数据集对ViSNet模型进行预训练,最终通过对预训练的ViSNet网络进行fine tuning,得到高准确度的预测结果。为了了解这份成果背后的技术,我开始阅读了相关的论文,首先阅读的是ViSNet,论文标题为
ViSNet: a scalable and accurate geometric deep learning potential for molecular dynamics simulation 。
论文:https://arxiv.org/abs/2210.16518
源码:没找到直接的源码,找到了相关另一篇文章的源码。内容大致相同。GitHub - microsoft/ViSNet at OGB-LSC@NIPS2022
背景介绍
分子动力学模拟(MD)描述了分子系统的动力学和热力学性质。它广泛应用于物理、化学、生物和制药领域。过去主要采用以下两种模拟方法:
- 从头算分子动力学模拟,例如由密度泛函理论 (DFT) 驱动的模拟。其优点是可以精确计算能量和力,但计算成本高昂,限制了其在大型分子系统和长时间模拟中的应用。
- 采用经验力场的经典 MD 可以进行快速且合适的模拟,因为它们适用于大型系统,但电子运动引起的量子效应无法捕获,力场参数通常不可转移。
近年来随着机器学习(ML)和深度学习(DL)的发展,由于其强大的特征提取能力和表示能力,得到越来越多的关注。特别是对数据依赖度更低的几何深度学习方法(GDL),GDL通过纳入分子的几何信息使模型对数据保持旋转平移不变性。尽管神经网络模型的预测精度已经接近传统的模拟方法,但任然存在几何信息利用不足和高计算成本的问题,这阻碍了它们在分子动力学模拟中的应用。为了缓解上上面的问题,文章作者提出了一种名为 ViSNet 的可扩展且高精度的分子动力学图深度学习模型。在ViSNet中,作者提出了一种运行时几何计算(RGC)策略,以线性计算复杂度提取和编码角度和二面体信息,显着加速模型训练和推理并减少内存消耗。然后,设计了一种新颖有效的矢量-标量交互式等变消息传递机制,称为 ViS-MP,通过将矢量表示与标量表示交互来充分利用几何信息。通过合并这两个模块,结合了两种类型 EGNN 各自的优点,使计算效率更高且几何信息也得到了更充分利用。在一些基准上进行综合评估时,ViSNet 在 MD17 数据集上的所有分子上均优于所有最先进的算法,并且在 QM9 数据集上表现出优越的性能,表明分子几何表示的强大能力。
模型架构
概述
如图 1(a)所示,ViSNet模型由一个embedding块和多个堆叠的 ViSNet 块组成,后面加上一个输出块。首先,embedding块把分子中各原子信息和化学键信息嵌入成向量,然后混合分子中的几何信息一起输入ViSNet块中聚合和更新。更新后的分子表示就包含了几何信息,然后这样的分子表示就可以在不同的输出块下进行各种下游任务了。其中每个ViSNet块由Message Block和Message Block组成,连续的两个ViSNet块之间有残差链接。

嵌入快
它首先嵌入原子,并通过径向基函数(RBF)计算其距离在截止范围内的边缘表示。然后将原子 i 的初始嵌入、其 1 跳邻居 j 和边 eij 融合在一起,作为初始节点嵌入 ![]() 和边嵌入
和边嵌入 ![]() 。嵌入块表示式:
。嵌入块表示式:
![]()
![]() 表示节点i的1跳邻居节点集合,j是其邻居之一。初始向量嵌入
表示节点i的1跳邻居节点集合,j是其邻居之一。初始向量嵌入 ![]() 设置为
设置为 ![]() 。向量嵌入
。向量嵌入 ![]() 通过投影到嵌入空间中。
通过投影到嵌入空间中。
Message Block
分子表示聚合:如下面参考图左边表示,从上一模块得到的分子表示通过函数 φ s m 聚合更新,表示式如下:
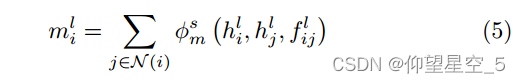
其中![]() 是块的索引,
是块的索引,![]() 是节点i在第l层的嵌入向量,
是节点i在第l层的嵌入向量,![]() 表示在第l层节点i和节点j之间的边特征。
表示在第l层节点i和节点j之间的边特征。
几何信息聚合:几何信息的聚合同分子表示聚合类似,如下面参考图右边所示,表示式如下:
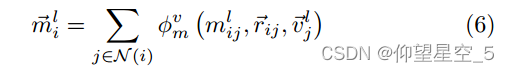
其中![]() 表示聚合j特征的i节点的特征表示。
表示聚合j特征的i节点的特征表示。![]() 表示节点 i 到其相邻节点 j 的方向向量。
表示节点 i 到其相邻节点 j 的方向向量。![]() 是节点i的“方向单元”,保留了节点i的几何信息,是从节点 i 到其所有相邻节点 j 的所有单位向量的总和,表示式如下:
是节点i的“方向单元”,保留了节点i的几何信息,是从节点 i 到其所有相邻节点 j 的所有单位向量的总和,表示式如下:
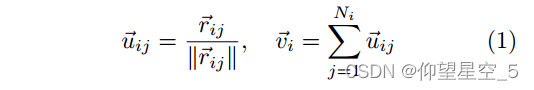
![]() 是
是 ![]() 的单位向量。
的单位向量。
参考图:

Message Block
更新节点的嵌入向量:完整的分子表示除了需要融合周围邻居点的特征 之外,还需融合原子周围的空间信息。融合的方法如下面展示图左侧,表示式如下式(7),通过聚合函数![]() 融合原子的原始特征和聚合特征,还有原子的方向单位向量
融合原子的原始特征和聚合特征,还有原子的方向单位向量![]() 的内积。
的内积。
![]()
另外,结合上面方程式(1)计算节点i的方向单位向量![]() 的内积,可以满足下式:
的内积,可以满足下式:
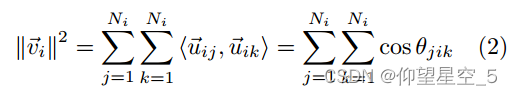
即,方向单位向量![]() 的内积等于节点i与其任意两个相邻节点所形成的所有角度的余弦值之和。其中
的内积等于节点i与其任意两个相邻节点所形成的所有角度的余弦值之和。其中 表示节点i到其所有邻居节点的单位向量内积之和。
表示节点i到其所有邻居节点的单位向量内积之和。

更新边的嵌入向量:和节点特征更新一样,边的特征更新也需要融合空间信息。融合的方法如上图右侧,表示式如下式(8)。
![]()
其中fij是边的原始特征,![]() 表示节点i的方向单元向量
表示节点i的方向单元向量![]() 在节点 i 到其相邻节点 j 的方向向量的投影。按照几何的运算规则,可以满足下式(3,4)
在节点 i 到其相邻节点 j 的方向向量的投影。按照几何的运算规则,可以满足下式(3,4)
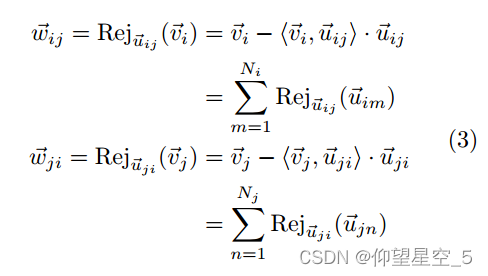
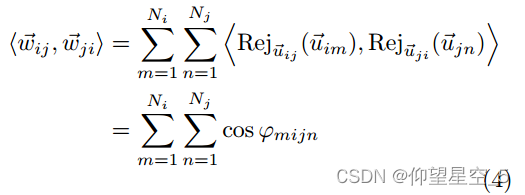
![]() 和
和 ![]() 在上面等式1中定义,是
在上面等式1中定义,是 ![]() 的单位向量。
的单位向量。![]() 表示m,I,j,n四个节点形成的二面角。可以参考图C进行理解。
表示m,I,j,n四个节点形成的二面角。可以参考图C进行理解。

更新节点的“方向单元”向量:节点方向单元向量的更新需要聚合原始方向单元向量![]() ,聚合周边节点特征后的节点特征
,聚合周边节点特征后的节点特征![]() 和聚合几何信息后的方向单元向量
和聚合几何信息后的方向单元向量![]() 。表示式如下式(9):
。表示式如下式(9):
![]()
这篇关于论文笔记|百度AI制药大赛冠军背后的技术(ViSNet)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







