Inkscape到OpenSCAD几何造型

Inkscape到OpenSCAD几何造型

    英文参考 - http://libregraphicsworld.org/blog/entry/inkscape-gets-openscad-converter

    在OpenSCAD的模型中，对于复杂的草图（如手绘、文字等），可以通过Inkscape绘制，然后输出为scad格式，再通过旋转、拉长等方式创建立体几何对象。这可以通过path2openscad插件来实现。

（1）Inkscape到OpenSCAD转换插件

A、插件下载

      点击这里下载 https://www.thingiverse.com/thing:25036/#files

B、插件安装

      解压缩下载后的文件：

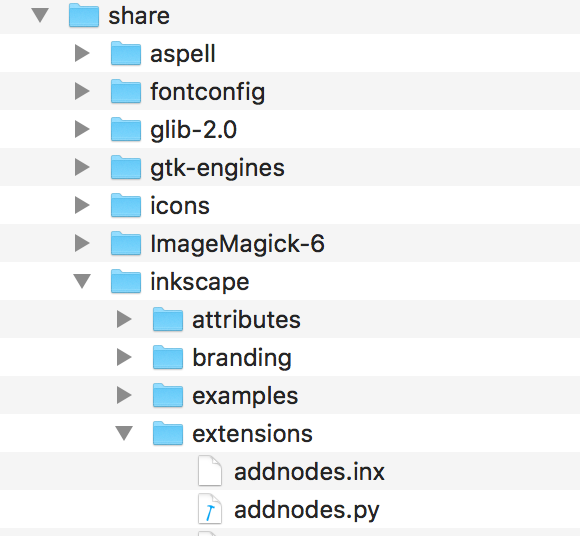
    将path2openscad-6里的两个文件path2openscad.inx和path2openscad.py复制到share/inkscape/extensions目录里面。

    在MacOS上，操作方法为：点击“应用程序”，右键选择“打开内容”，再选择inkscape，到share/inkscape/extensions目录，把上面的最新版本的*.inx和*.py文件拷贝到extensions目录下。

    然后，关闭并重新启动inkscape即可。

C、插件使用

    该扩展插件将自动从inkscape模型挤出为三维的OpenSCAD的.scad 模型文件，需要下面两个步骤。

    1. 选择对象，然后使用菜单Extensions / Generate from Path / Paths to OpenSCAD 项.

    OpenSCAD 转换器有多个选项，如果不选择对象，将输出本页的所有几何对象。 

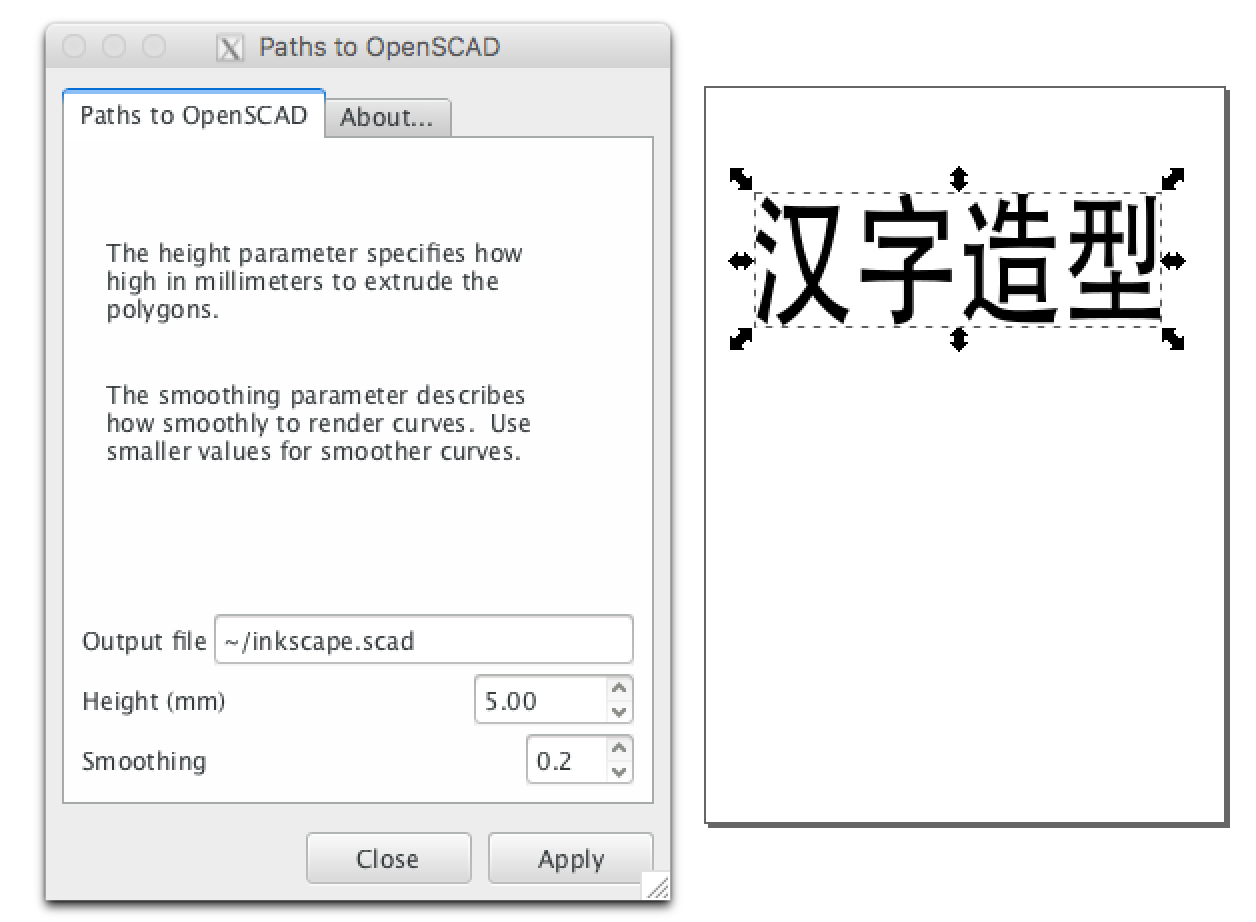
    2. 填写输出文件路径, 选择挤出的宽度，然后点击 Apply.

    到 OpenSCAD 中打开文件，然后按 F5 进行渲染.

    这个流程是比较简单的，像 in this case 可以把照片转为 3D 打印的珠宝，搞起来就有一点点头疼了。

（2）三维造型处理

    在OpenSCAD中可以旋转、拉伸、挤出（单向挤出、旋转挤出）等操作对几何对象进一步修改。

    具体参见OpenSCAD文档：

• 几何对象的循环、挤出与排列：http://www.tridimake.com/2014/11/howto-openscad-iteration-extrusion.html
• 几何对象造型语言参考-http://www.openscad.org/documentation.html