本文主要是介绍Unit2_2:动态规划DP,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 一、最长公共子序列
- 分析
- 填表
- 伪代码
- 过程
- 时间复杂度
- 二、最长公共子串问题
- 分析
- 过程
- 时间复杂度
- 最小编辑距离
- 背景
- 分析
- 状态转移方程
- 填表
- 伪代码
- 案例
一、最长公共子序列
子序列:指从原序列中选取出来的具有相对顺序的一组元素,而这些元素不一定是连续的。

X和Y的最长公共子序列是Z。
分析
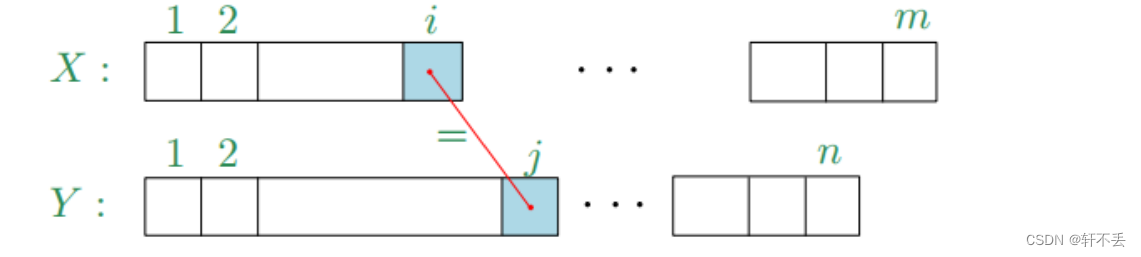
设 Z k = ( z 1 , . . . , z k ) Z_k=(z_1,...,z_k) Zk=(z1,...,zk)为 X [ 1.. i ] X[1..i] X[1..i]和 Y [ 1.. j ] Y[1..j] Y[1..j]的最长公共子序列( L C S LCS LCS),最大值用 d i , j d_{i,j} di,j表示
若 x i = y j ,则 z k = x i = y j ,且 z k − 1 是 X [ 1.. i − 1 ] 和 Y [ 1.. j − 1 ] 的 L C S 。 若x_i = y_j,则z_k = x_i = y_j,且z_{k−1}是X[1..i−1]和Y[1..j−1]的LCS 。 若xi=yj,则zk=xi=yj,且zk−1是X[1..i−1]和Y[1..j−1]的LCS。
若 x i ≠ y j ,这意味着 L C S 不以 x i 结束,也不以 y j 结束。 那么 Z k 要么是 X [ 1.. i − 1 ] 和 Y [ 1.. ] j ] 的 L C S ,或 X 的 L C S [ 1.. i ] 和 Y [ 1.. j − 1 ] 。 我们继续使用两种情况下更大的 L C S 计数。 若xi \neq yj,这意味着LCS不以xi结束,也不以yj结束。\\ 那么Z_k要么是X [1..i−1]和Y[1..]j]的LCS,或X的LCS [1..i]和Y [1..j−1]。\\我们继续使用两种情况下更大的LCS计数。 若xi=yj,这意味着LCS不以xi结束,也不以yj结束。那么Zk要么是X[1..i−1]和Y[1..]j]的LCS,或X的LCS[1..i]和Y[1..j−1]。我们继续使用两种情况下更大的LCS计数。
因此可得:
d i , j = { d i − 1 , j − 1 + 1 i f x i = y i m a x ( d i − 1 , j , d i , j − 1 ) i f x i ≠ y i d_{i,j}=\left\{ \begin{array}{ll} d_{i-1,j-1} +1& if \space x_i=y_i \\ max ( d_{i-1,j} , d_{i,j-1} )& if \space x_i \neq y_i \nonumber \end{array} \right. di,j={di−1,j−1+1max(di−1,j,di,j−1)if xi=yiif xi=yi
填表
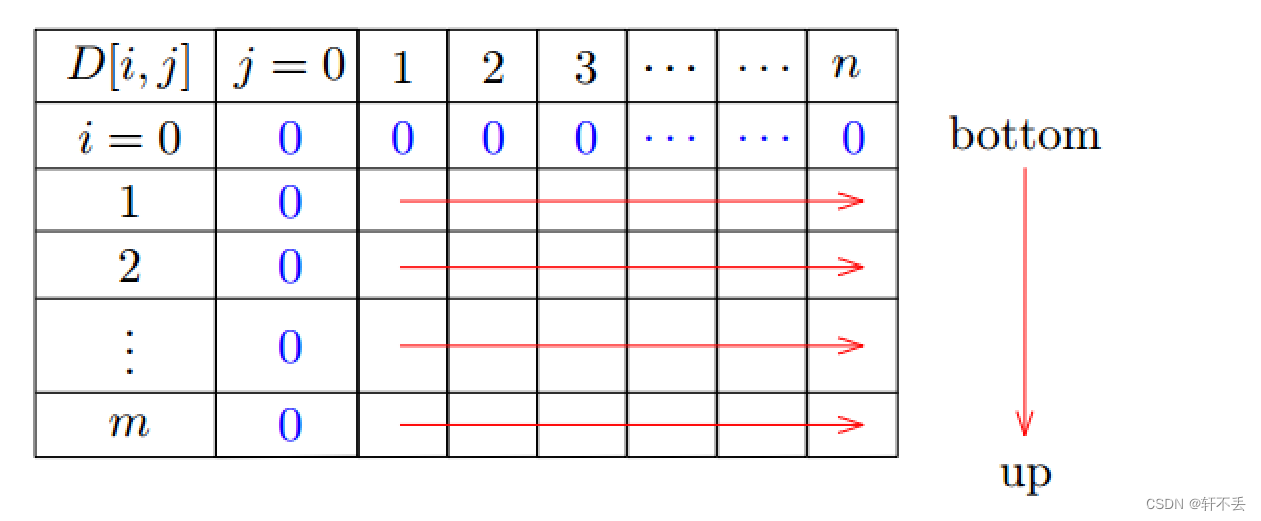
同样,我们创建另一个 m × n m×n m×n矩阵 p [ i , j ] p[i, j] p[i,j],对于 1 ≤ i ≤ m ,且 1 ≤ j ≤ n 1≤i≤m,且1≤j≤n 1≤i≤m,且1≤j≤n,来存储指向计算中使用的元素的箭头。因此,我们可以稍后重建 L C S LCS LCS的元素
伪代码
Longest-Common-Subsequence(X,Y)
//Initialization
for i ← 0 to m dod[i,0] ← 0
end
for j ← 0 to m dod[0,j] ← 0
end//Dynamic Programming
for i ← 0 to m dofor j ← 0 to m doif xi = yi thend[i,j] ← d[i-1,j-1]+1p[i,j]="LU" //"LU" indicates left up arrowendendelse if d[i-1,j] >= d[i,j-1] thend[i,j] ← d[i-1,j]p[i,j]="U" //"U" indicates up arrowendelsed[i,j] ← d[i,j-1]p[i,j]="L" //"L" indicates left arrowend
end
return d,p
Print-LCS(p,X,i,j)
if i is equal to 0 or j is equal to 0 thenreturn NULL;
end
if p[i,j] is equal to "LU” thenPrint-LCS(p,X,i-1,j-1);print xi;
end
else if p[i,j] is equal to "U” thenPrint-LCS(p,X,i-1,i);
end
elsePrint-LCS(p,X,i,j-1);
end
过程
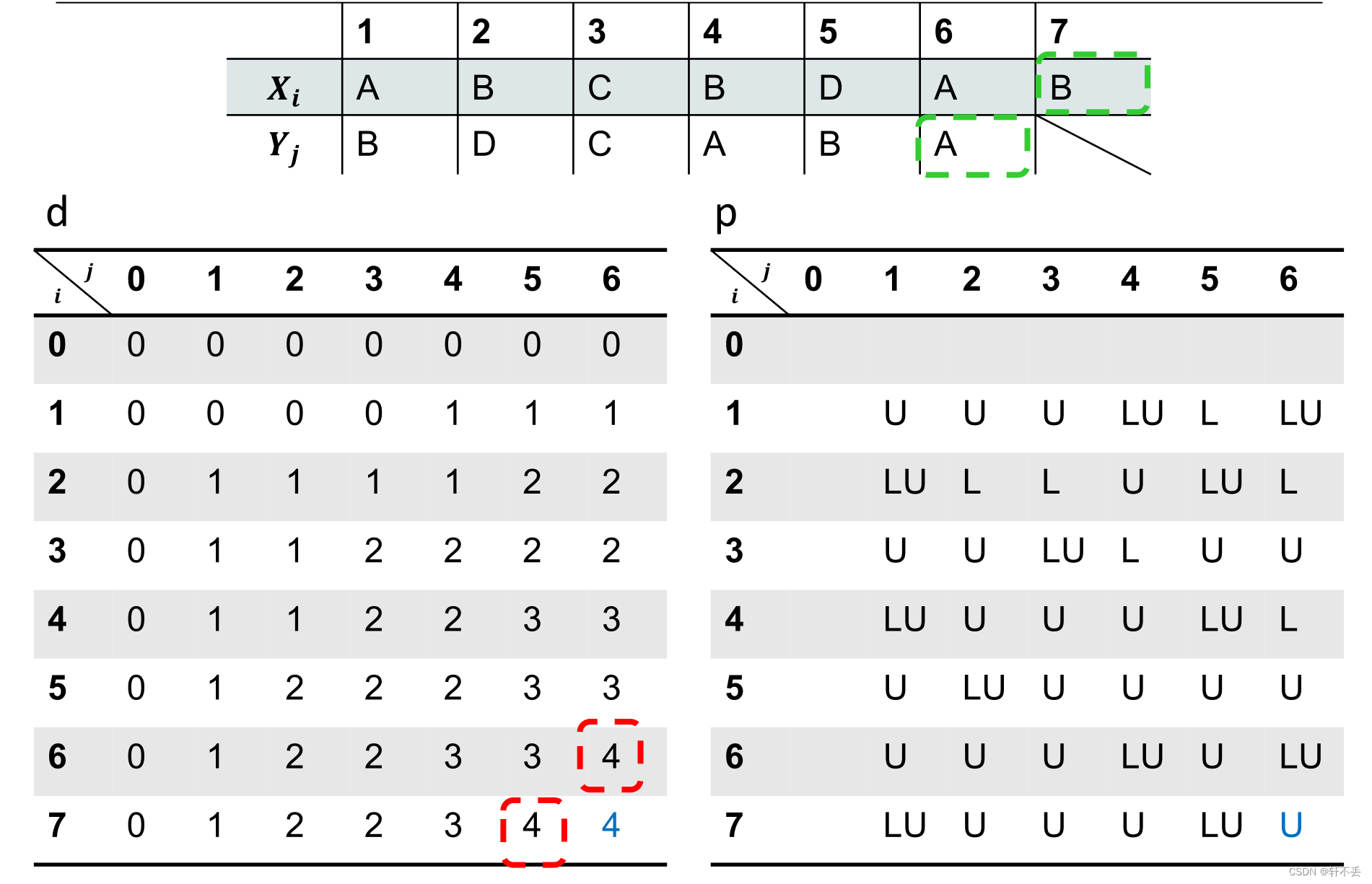
然后根据p的指示找出最长公共子序列即可
时间复杂度
两层循环,时间复杂度 T ( n ) = O ( n m ) T(n)=O(nm) T(n)=O(nm)
二、最长公共子串问题
子串:指从原序列中选取出来的具有相对顺序的一组元素,而且这些元素一定是连续的。

分析
此题和上一个 L C S LCS LCS不同,不能设 Z k = ( z 1 , . . . , z k ) Z_k=(z_1,...,z_k) Zk=(z1,...,zk)为 X [ 1.. i ] X[1..i] X[1..i]和 Y [ 1.. j ] Y[1..j] Y[1..j]的最长公共子串( L C S LCS LCS),最大值用 d i , j d_{i,j} di,j表示。因为以此结尾的 x i 和 y j x_i和y_j xi和yj若相同, d i , j d_{i,j} di,j也不一定等于 d i − 1 , j − 1 + 1 d_{i-1,j-1}+1 di−1,j−1+1,可能字串在中间,无法递归。
DP无法进行下去时可以加以限制,我们只需要定义 Z k = ( z 1 , . . . , z k ) Z_k=(z_1,...,z_k) Zk=(z1,...,zk)为 X [ 1.. i ] X[1..i] X[1..i]和 Y [ 1.. j ] Y[1..j] Y[1..j]的以 x i x_i xi或和 y j y_j yj结尾的最长公共子串( L C S LCS LCS),最大值用 d i , j d_{i,j} di,j表示,此时就能递归进行下去了。
若 x i = y j ,则 z k = x i = y j ,且 z k − 1 是 X [ 1.. i − 1 ] 和 Y [ 1.. j − 1 ] 的 L C S 。 若x_i = y_j,则z_k = x_i = y_j,且z_{k−1}是X[1..i−1]和Y[1..j−1]的LCS 。 若xi=yj,则zk=xi=yj,且zk−1是X[1..i−1]和Y[1..j−1]的LCS。
若 x i ≠ y j ,这意味着 L C S 不以 x i 结束,也不以 y j 结束。 若xi \neq yj,这意味着LCS不以xi结束,也不以yj结束。 若xi=yj,这意味着LCS不以xi结束,也不以yj结束。
d i , j = { d i − 1 , j − 1 + 1 i f x i = y i 0 i f x i ≠ y i d_{i,j}=\left\{ \begin{array}{ll} d_{i-1,j-1} +1& if \space x_i=y_i \\ 0& if \space x_i \neq y_i \nonumber \end{array} \right. di,j={di−1,j−1+10if xi=yiif xi=yi
最后,我们可以通过计算所有可能的结束位置i和j的最大值来得到最长的公共子串。
L C S ( X , Y ) = m a x ( d i , j ) LCS(X,Y)=max(d_{i,j}) LCS(X,Y)=max(di,j)
填表也是一致
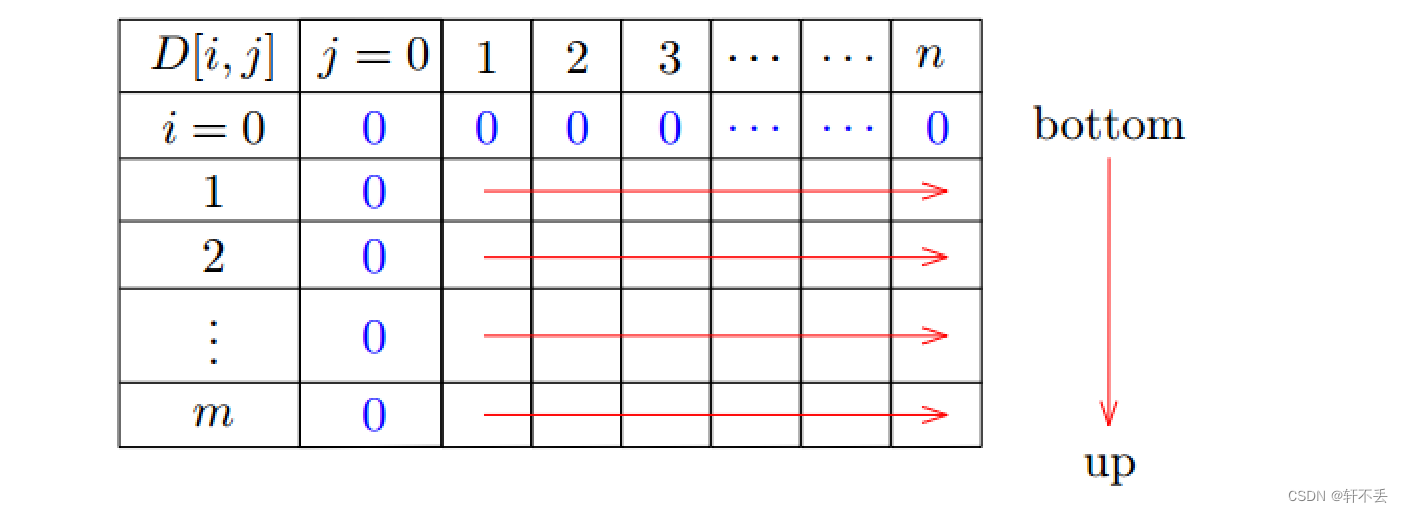
但这里维护位置就很简单了,因为子串是连续的,因此只需要记录末尾位置和最大长度即可:用 l m a x l_{max} lmax和 p m a x p_{max} pmax分别存储公共子字符串的最大长度及其位置i(或j)。所以,我们可以稍后从X(或Y)重建元素。
Longest-Common-Substring(X,Y)
//Initialization
lmax ← 0
pmax ← 0
for i ← 0 to m dod[i,0] ← 0
end
for j ← 0 to n dod[0,j] ← 0
end//Dynamic Programming
for i ← 1 to m dofor j ← 1 to n doif xi != yi thend[i,j] ← 0endelsed[i,j] ← d[i-1,j-1]if d[i,j]>lmax thenlmax ← d[i,j]pmax ← iendendendend
return lmax,pmax
Print-LCS(X,lmax,pmax)
if lmax is equal to 0 thenreturn NULL;
end
for i ← (pmax-lmax+1) to pmax doprint xi
end
过程
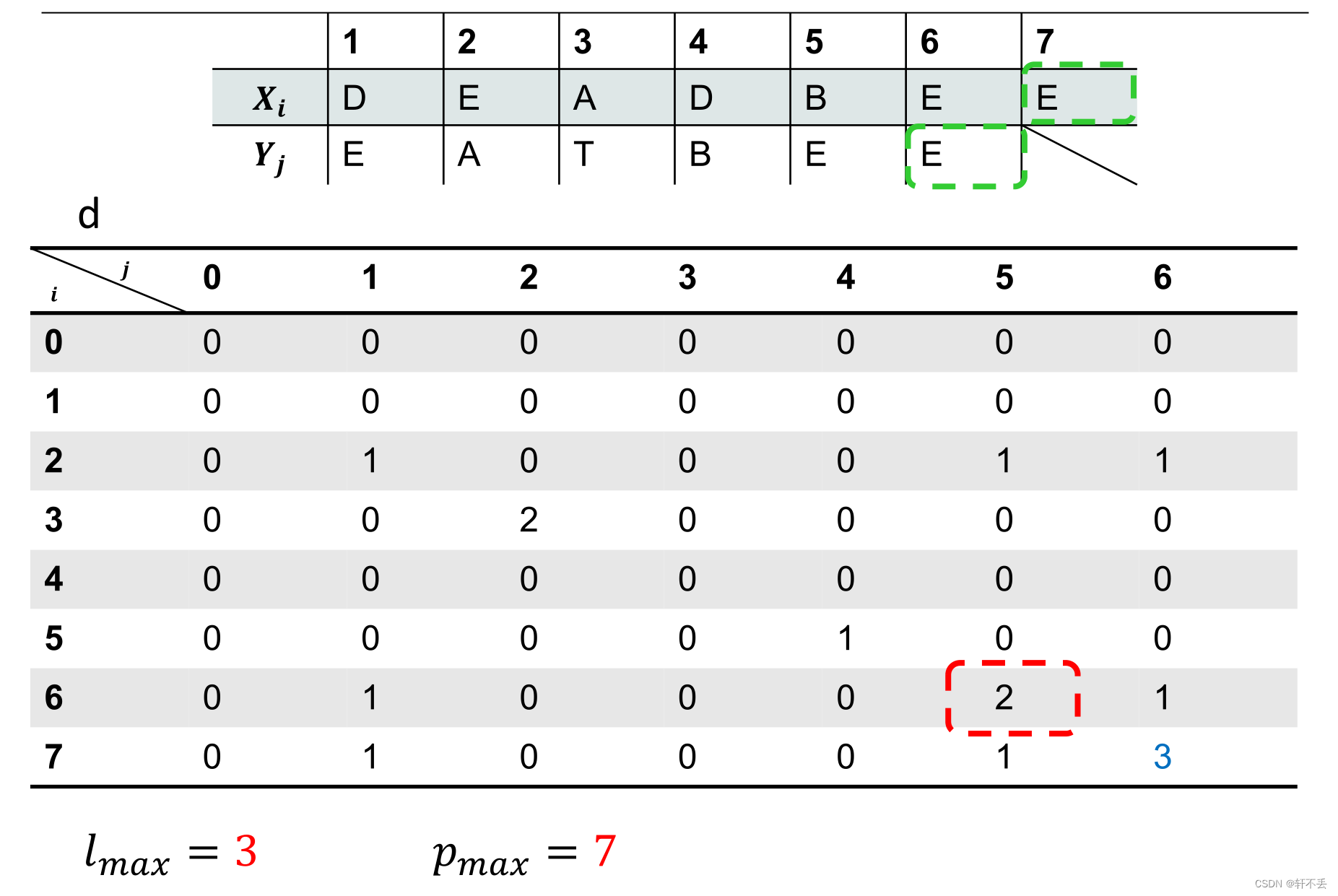
时间复杂度
两层循环,时间复杂度 T ( n ) = O ( n m ) T(n)=O(nm) T(n)=O(nm)
最小编辑距离
背景
当把“algorithm”误输入为“algorithm”时,系统可能自动帮助搜索最优的调节词矫正。可运用于机器翻译,信息提取和语音识别。
给定两个数组 X = ( x 1 , x 2 , . . . , x m ) , Y = ( y 1 , y 2 , . . . , y n ) 给定两个数组X=(x_1,x_2,...,x_m),Y=(y_1,y_2,...,y_n) 给定两个数组X=(x1,x2,...,xm),Y=(y1,y2,...,yn),编辑距离是将X转换为Y的编辑操作的最小次数
分析
编辑一共有三种操作:
添加字母
删除字母
替换一个字符。
因为实际考虑中每个操作都需要付出相应的代价 c o s t cost cost,为了简化问题,设每个操作 c o s t = 1 cost=1 cost=1
定义 D [ i , j ] 为子字符串 X [ 1.. i ] 和 Y [ 1.. j ] 的最小编辑距离 定义D[i,j]为子字符串X[1..i]和Y [1..j]的最小编辑距离 定义D[i,j]为子字符串X[1..i]和Y[1..j]的最小编辑距离
将 X [ 1.. i ] 变成 Y [ 1.. j ] X[1..i]变成Y [1..j] X[1..i]变成Y[1..j]有三种情况:
将 X [ 1.. i − 1 ] 变成 Y [ 1.. j ] X[1..i-1]变成Y [1..j] X[1..i−1]变成Y[1..j]并删除 X [ i ] X[i] X[i]
M E D ( c x y − > d a b ) = M E D ( c x − > d a b ) + 1 MED(cxy->dab)=MED(cx->dab)+1 MED(cxy−>dab)=MED(cx−>dab)+1
将 X [ 1.. i ] 变成 Y [ 1.. j − 1 ] X[1..i]变成Y [1..j-1] X[1..i]变成Y[1..j−1]并插入Y[j]
M E D ( c x y − > d a b ) = M E D ( c x y − > d a ) + 1 MED(cxy->dab)=MED(cxy->da)+1 MED(cxy−>dab)=MED(cxy−>da)+1
如果 X [ i ] ≠ Y [ j ] X[i] \neq Y[j] X[i]=Y[j],将 X [ 1.. i − 1 ] 变成 Y [ 1.. j − 1 ] X[1..i-1]变成Y [1..j-1] X[1..i−1]变成Y[1..j−1]并将 X [ i ] 替换成 Y [ j ] X[i]替换成Y[j] X[i]替换成Y[j]
M E D ( c x y − > d a b ) = M E D ( c x − > d a b ) + 1 MED(cxy->dab)=MED(cx->dab)+1 MED(cxy−>dab)=MED(cx−>dab)+1
M E D ( c x y − > d a b ) = M E D ( c x − > d a ) + 1 MED(cxy->dab)=MED(cx->da)+1 MED(cxy−>dab)=MED(cx−>da)+1
状态转移方程
D [ i , j ] = m i n { D [ i − 1 , j ] + 1 D [ i , j − 1 ] + 1 D [ i − 1 , j − 1 ] + { 0 i f X [ i ] = Y [ j ] 1 i f X [ i ] ≠ Y [ j ] D[i,j]=min\left\{ \begin{array}{ll} D[i-1,j] +1\\ D[i,j-1] +1\\ D[i-1,j-1]+\left\{ \begin{array}{ll} 0 & if \space X[i]=Y[j]\\ 1 & if \space X[i] \neq Y[j] \nonumber \end{array} \right.\nonumber \end{array} \right. D[i,j]=min⎩ ⎨ ⎧D[i−1,j]+1D[i,j−1]+1D[i−1,j−1]+{01if X[i]=Y[j]if X[i]=Y[j]
同时,我们创建另一个矩阵 p [ i , j ] ( 1 ≤ i ≤ m , 1 ≤ j ≤ n ) p[i, j](1≤i≤m, 1≤j≤n) p[i,j](1≤i≤m,1≤j≤n)来存储指向计算中使用的元素的箭头,用于恢复操作的最优序列。
p [ i , j ] = { L e f t i f I n s e r t i o n U p i f D e l e t i o n L e f t U p i f S u b s t i t u t i o n p[i,j]=\left\{ \begin{array}{ll} Left& if \space Insertion\\ Up& if \space Deletion\\ Left Up& if \space Substitution \nonumber \end{array} \right. p[i,j]=⎩ ⎨ ⎧LeftUpLeftUpif Insertionif Deletionif Substitution
填表
最初,我们用 j j j填充矩阵 D [ 0 , j ] D[0,j] D[0,j]的第一行,用 i i i填充矩阵 D [ i , 0 ] D[i, 0] D[i,0]的第一列。
空串到一个长为 j j j的串或者长为 i i i的串到空串,最短做法就是一个个删除或者添加。
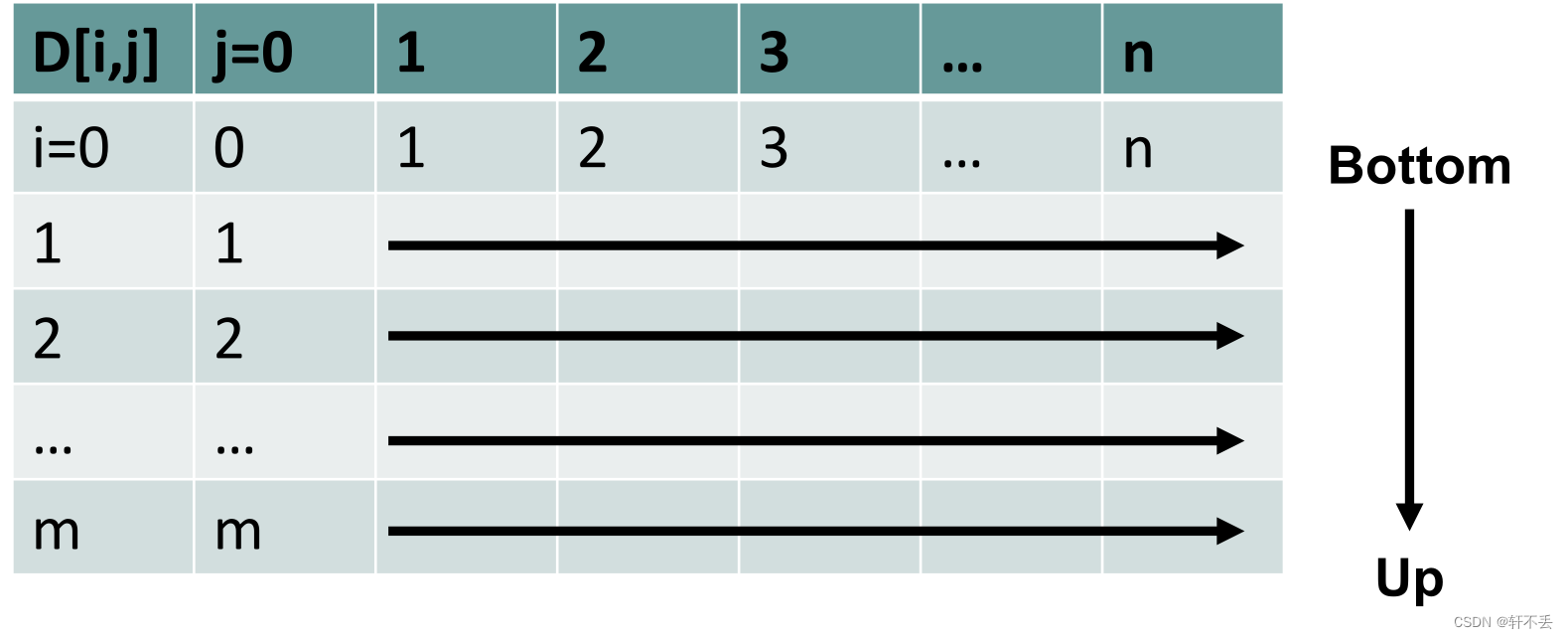
伪代码
Minimum-Edit-Distance(X,Y)
//Initialization
for i ← 0 to m dod[i,0] ← ip[i,0]="U'
end
for j ← 0 to m dod[0,j] ← jp[0,j]="L"
end//Dynamic Programming
for i ← 1 to m dofor j ← 1 to n doif xi != yi thenc ← 1endelsec ← 0endif d[i-1][j-1]+c <= d[i-1][j]+1 andd[i-1][j-1]+c <= d[i][j-1]+1 thend[i][j] ← d[i-1][j-1]+cp[i][j] ← "LU"endelse if d[i-1][j]+1 <= d[i-1][j-1]+c andd[i-1][j]+1 <= d[i][j-1]+1 thend[i][j] ← d[i-1][j]+1p[i][j] ← "U"endelsed[i][j] ← d[i][j-1]+1p[i][j] ← "L"endendreturn d,p
end
Print-MED(p,X,i,j)
if i is equal to 0 or j is equal to 0 thenreturn NULL;
end
if p[i,j] is equal to "LU” thenPrint-MED(p,X,i-1,j-1);if xi = yi thendo nothingendelseprint Substitue xi with yiend
end
else if p[i,j] is equal to "U” thenPrint-MED(p,X,i-1,i);print Delete xi
end
elsePrint-MED(p,X,i,j-1);print Insert xi
end
案例
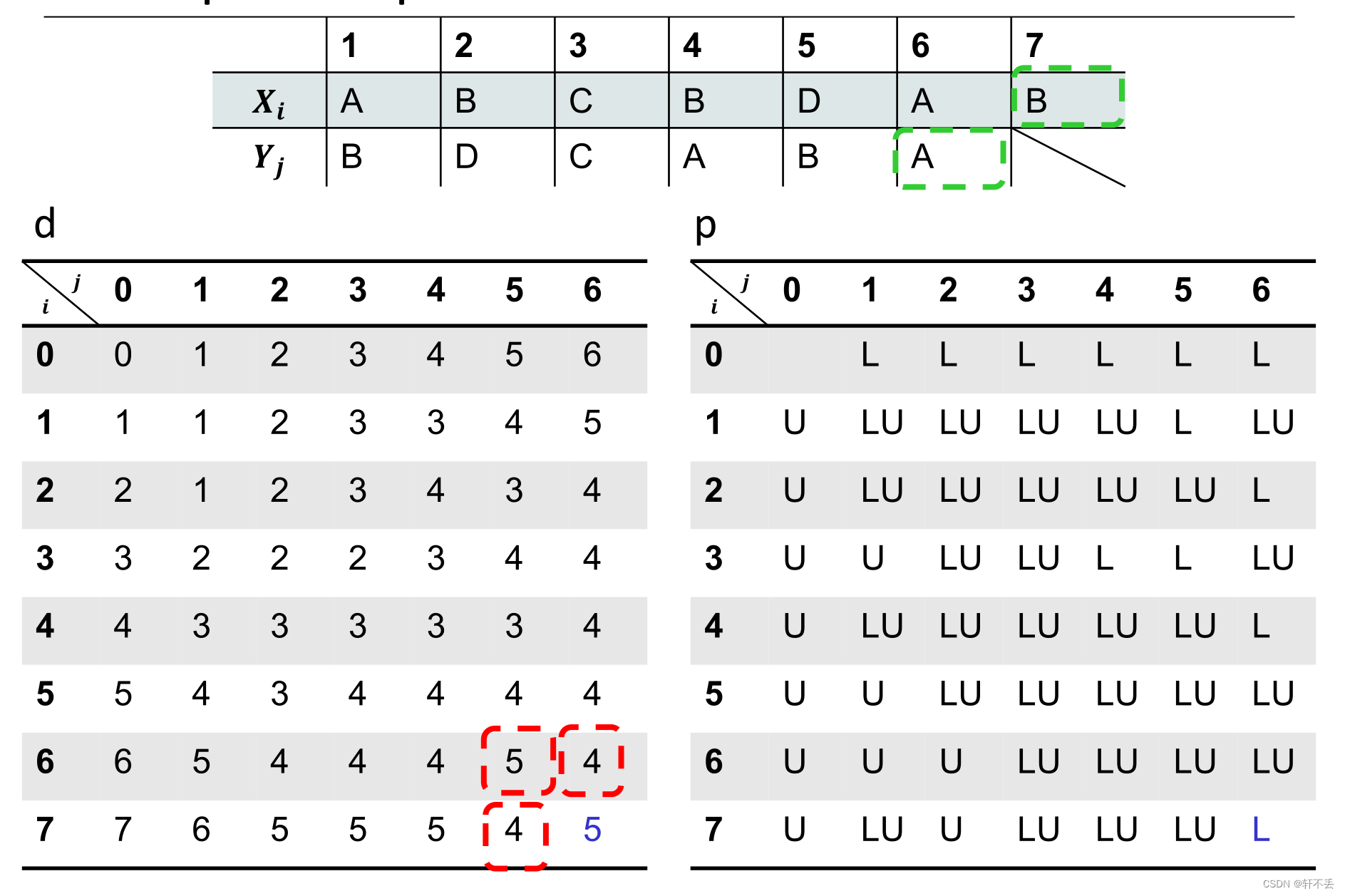
根据P找到具体操作路径
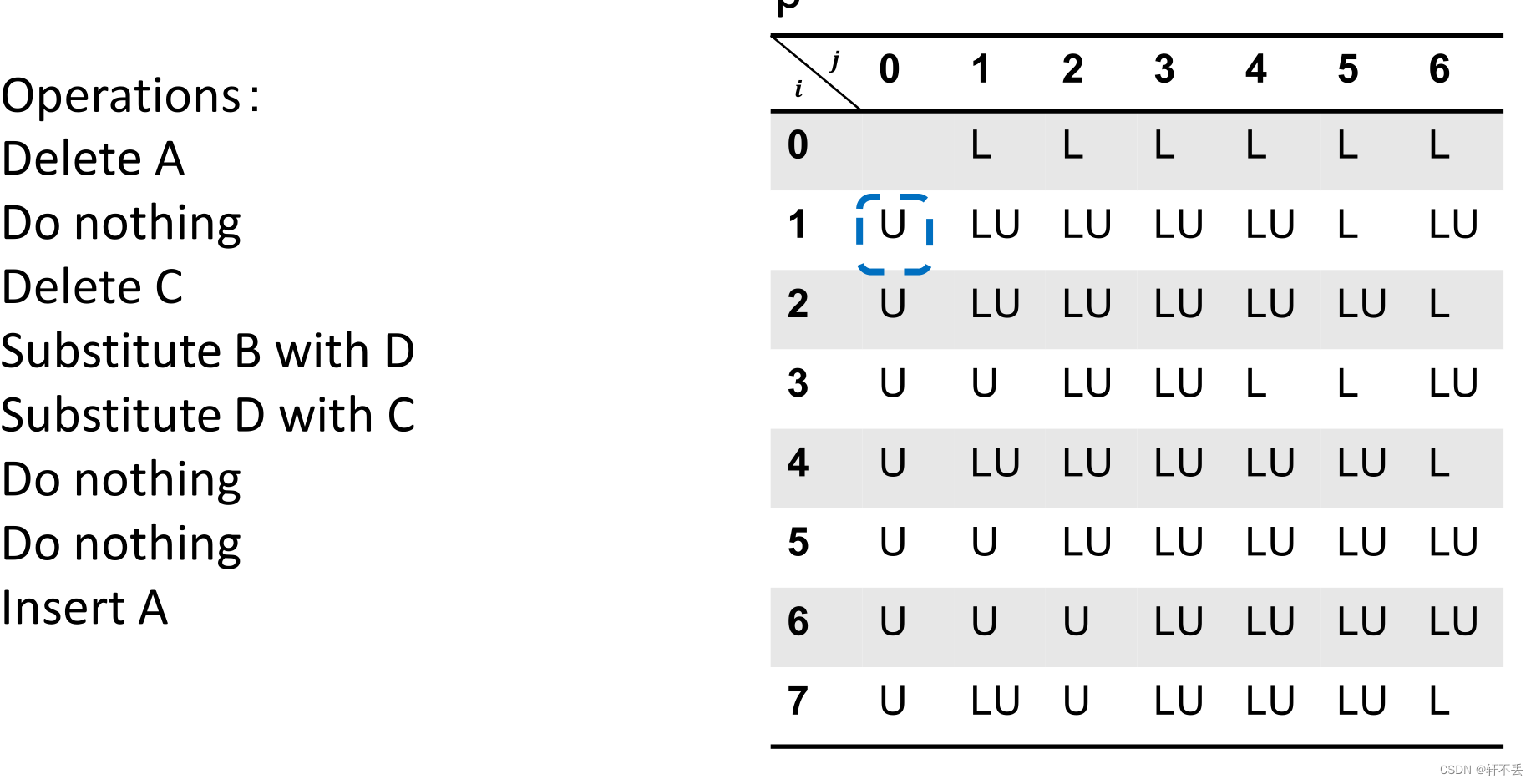
这篇关于Unit2_2:动态规划DP的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




