了解传递函数中的极点和零点

原文链接

Robert Keim

之前提出了两种标准方法来为一阶RC低通滤波器制定s域传递函数。简要回顾一些基本概念：传递函数在数学上表示滤波器的频域输入到输出行为；可以用变量s来表示传递函数，它代表复杂的频率，当需要计算特定频率的幅度和相位响应时可以用jω代替s ；传递函数的标准化形式就像一个模板，可以帮助我们快速确定滤波器的定义特征；对标准化一阶传递函数的数学处理使我们能够证明滤波器的截止频率是幅度减小3dB并且相位偏移-45°的频率。

极点和零点

假设我们有一个传递函数，其中变量s出现在分子和分母中。在这种情况下，至少一个s值将使分子为零，并且至少一个s值将使分母为零。使分子为零的值是传递函数零点，并且使分母为零的值是传递函数极点。让我们考虑以下示例：

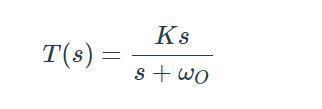
在这个系统中，在s=0时为零点，在s=–ωo时为极点。极点和零点定义了滤波器的特征。如果你知道极点和零点的位置，则可以获得有关系统如何响应不同输入频率的信号的信息。

极点和零点的影响

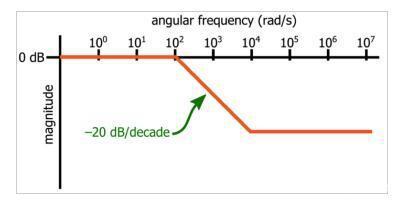
波特图提供了极点或零点与系统输入与输出行为之间关系的直观可视化。极点频率对应于角频率，在该角频率处，振幅曲线的斜率减小20dB /decade，并且一个零点对应于一个角斜率，在该频率下，斜率增加20dB /decade。在下面的示例中，波特图是系统的振幅响应的近似值，该系统的极点为10 2弧度/秒（rad / s），零点为10 4 rad / s。

相位效应

在上一篇文章中，我们看到低通滤波器的相位响应的数学原点是反正切函数。如果我们使用反正切函数（更具体地是负反正切函数）来生成相位（以度为单位）与对数频率的关系图，最终得到以下曲线：

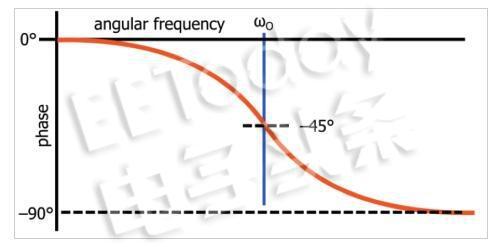
由极点产生的相移的波特图近似是表示相移的-90°的直线。该线以极点频率为中心，并且每十倍频率下具有-45度的斜率，这意味着向下倾斜的线在极点频率之前十倍频率开始并且在极点频率之后十倍频率结束。除了线具有正斜率之外，零点影响是相同的，使得总相移是+ 90°。以下示例表示一个系统，其极点为10 2 rad / s，零点为10 5 rad / s。

隐藏的零点

低通滤波器的传递函数可以写成如下：

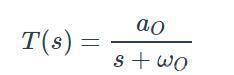
这个系统有零点吗？如果我们应用本文前面给出的定义，将得出结论，它不是变量s不出现在分子中，因此s的任何值都不会导致分子等于零。事实证明，它确实有一个零点，为了理解原因，我们需要考虑传递函数极点和零点更一般化的定义：零点（z）发生在s的值上，它导致传递函数减小到零，极点（p）发生在s的值上，导致传递函数趋向于无穷大：

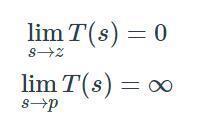
一阶低通滤波器的s值是否会导致T（s）→0？是的，即s =∞。因此，一阶低通系统在ωo处有极点，在ω=∞处有零点。尝试在ω=∞处提供零点的物理解释：它表示滤波器不能继续“永久”衰减（其中“永久”指的是频率，而不是时间）。如果设法创建一个输入信号，其频率继续增加直到达到无穷大rad / s，则s =∞时的零点会使滤波器停止衰减，即振幅响应的斜率从-20 dB /decade到0 dB /decade。

总结

我们已经探索了传递函数极点和零点的基本理论和实践方面，并且我们已经看到在滤波器的极点和零点频率及其振幅和相位响应之间建立直接关系。