本文主要是介绍条件概率、全概率、先验概率、后验概率,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
**
前言
**
条件概率,全概率,先验概率,后验概率这么多的定义,以前是几乎遇见一次都要百度一次,一看就会,然而没有做好总结下一次还是会忘掉,好记性终究敌不过烂笔头,这次做个总结,一劳永逸,个人愚见,请大家不吝赐教。
**
1.条件概率
**
首先上定义 :设A,B是两个事件,且P(B)>0,则在事件B发生的条件下,事件A发生的条件概率为:
P(A|B)=P(AB)/P(B)
一般说到条件概率这一概念的时候,事件A和事件B都是同一实验下的不同的结果集合,事件A和事件B一般是有交集的,若没有交集(互斥),则条件概率为0,例如,我们我们掷骰子,掷出的点数为奇数称为事件A,扔出的点数为小(即1,2,3)称为事件B,问:B已经发生的条件下,A发生的概率是多少?
在这个实验中,事件A和事件B是有交集的,即1点和3点。
通过上面的例子,我们可以将条件概率的公式翻译为P(A|B)是在事件B发生概率的前提下,事件A的发生概率;P(AB)是发生的结果同时满足事件A和事件B的概率;P(B)是事件B发生的概率,不考虑事件A。在上面的例子中,P(A|B)即是骰子的点数是在满足事件B的点数1,2,3中选择满足事件A的点数,为1和3,所以P(A|B)为2/3;P(AB)是可能发生的六个点数中的1和3满足条件,则P(AB)为2/6;P(B)是可能发生的六个点数中的1、2、3满足条件,则P(B)为3/6。
**
2.全概率
**
定义:如果事件B1、B2、B3…Bn 构成一个完备事件组,即它们两两互不相容,其和为全集;并且P(Bi)大于0,则对任一事件A有:
P(A)=P(A|B1)P(B1) + P(A|B2)P(B2) + ... + P(A|Bn)P(Bn)
或者:p(A)=P(AB1)+P(AB2)+...+P(ABn))
其中A与Bn的关系为交。
还是来举个生动的栗子吧。
如下图 ,小张从家到公司上班总共有三条路可以直达,但是每条路每天拥堵的可能性不太一样,由于路的远近不同,选择每条路的概率如下:
P(L1)=0.5,P(L2)=0.3,P(L3)=0.2
每天上述三条路不拥堵的概率分别为:
P(C1)=0.2,P(C2)=0.4,P(C3)=0.7
假设遇到拥堵会迟到,那么小张从Home到Company不迟到的概率是多少?

其实不迟到就是对应着不拥堵,设事件C为到公司不迟到,事件为选择第i条路,则:
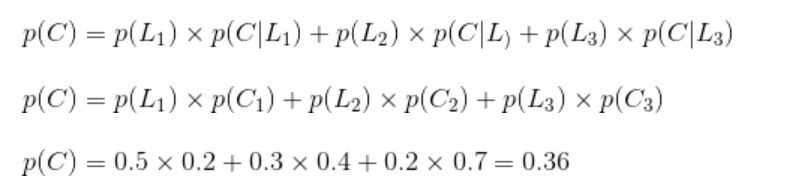
全概率就是表示达到某个目的,有多种方式(或者造成某种结果,有多种原因),问达到目的的概率是多少(造成这种结果的概率是多少)?
**
3.先验概率和后验概率
**
要搞清楚先验概率和后验概率的关系首先要明白一点,先验概率和后验概率都是强调一个原因,先验概率是指根据以往经验和分析得到的概率,如全概率公式,它往往作为"由因求果"问题中的"因"出现。比如,我们下面要用到的一个例子,一个人是帅哥的概率是多大,这个是我们通过观察身边的人,根据经验得出的概率,我个人感觉的话,十分之一差不多吧,通常中学一个班三十个男生应该有两三个称得上帅哥的吧,哈哈。
后验概率是指依据得到"结果"信息所计算出的最有可能是那种事件发生,如贝叶斯公式中的,是"执果寻因"问题中的"因"。比如我们听到有人八卦隔壁班的小强脱单了,是小红倒追的,虽然没有见过小强,你还是觉得小强应该是个帅哥,毕竟是倒追的嘛,哈哈。这就是一个简单的执果(小强脱单)寻因(小强是个帅哥)。
还是举个栗子来直观感受一下吧。
博主的室友小强脱单了,众所周知,在计算机学院高颜值,高资本和高超的编程能力都是脱单的利器。假设事件A为脱单,事件B1为高颜值,事件B2为收入高,事件B3为拥有高超的编程能力,那博主想知道的便是P(B1|A)的大小,则有:
P(B1|A)={P(A|B1)*P(B1)} / P(A)=P(AB1) / P(A)=P(A|B1)*P(B1) / {P(A|B1)*P(B1)+P(A|B2)*P(B2)+P(A|B3)*P(B3)}
在上面的公式当中,等号左边的P(A)便是先验概率,也可以表述为大学生在校脱单的概率,这个概率是一个经验值,或者也可以是经过统计调查出的一个参考值;等号右边的P(B1|A)便是后验概率,也就是博主希望得到的数值,表述为,已经知道小强脱单了,那么小强他的颜值是不是很高呢?
假如我们是新生,在新生群里找齐了自己的舍友并建立的舍群,晚上宿舍群里聊天,舍友甲说自己有女朋友,舍友乙说自己没有女朋友,那么虽然大家都还没有见过,那么你是不是就会有一种舍友甲应该比舍友乙长得帅一些的感觉,这个就是后验概率的结果。因为我们根据经验得出长得帅的人脱单的概率要大,所以我们潜意识里有了这个脱单的人比没有脱单的人长得好看的直觉,当然这个直觉并不一定准确。
参考:
https://blog.csdn.net/u010164190/article/details/81043856
https://blog.csdn.net/m0_38052384/article/details/93368629
这篇关于条件概率、全概率、先验概率、后验概率的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




