2.4 是否同一棵二叉搜索树（树，c）

04-树4 是否同一棵二叉搜索树

是否同一棵二叉搜索树

题意理解

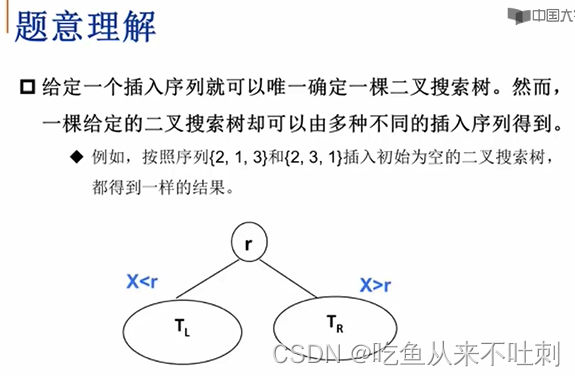
把一个序列插到一棵二叉搜索树里去，按顺序把每个数逐个插入到二叉搜索树里去

输入样例：

4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0

输出样例：

Yes
No
No

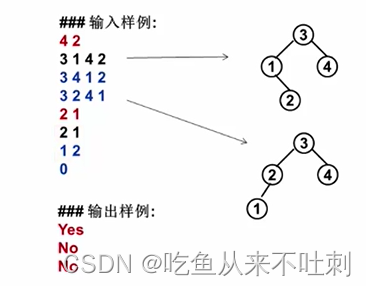
• 第一行两个整数，4是这个插入的序列的数的个数，也就是二叉搜索树的结点个数，2代表后面有两个序列需要和前面比较是不是一样
  第二行 代表输入第一组的序列
  第三、四行就代表后面若干组输入的序列，与第一组输入的序列作比较
• 第五行两个整数，2和1代表两个结点，比较一组
  第七行 代表输入第一组的序列
  第八行就代表后面若干组输入的序列，与第一组输入的序列作比较

求解思路

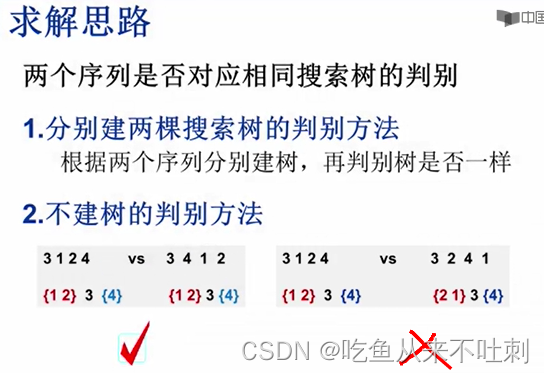
1用到递归，2是比较根结点左右值

搜索树表示

v表示节点的信息，阈flag判别一个序列是不是和树一致，某个结点没被访问过设为0，被访问过设为1，flag作为有没有被访问过的标记

程序框架的搭建

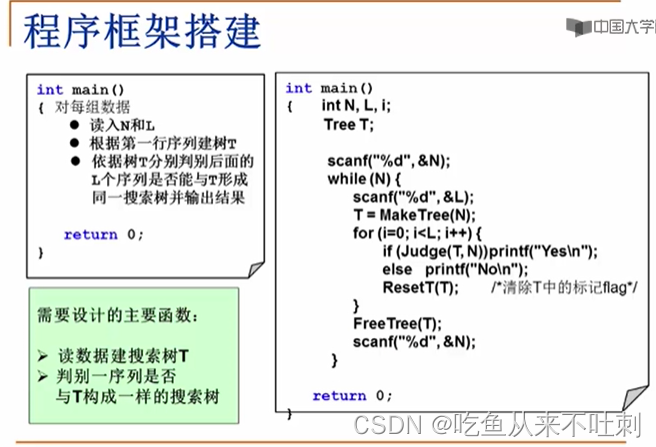
Judge读入树T，然后读入一个序列里的N个数，和T作比较，一致就返回yes
ResetT把树上每个标记flag都设为0
释放掉树，在读入下一组N，循环

如何建搜索树

构造新结点：NewNode申请一个新的结点的空间，然后把这个结点的结构的每个值给赋上，flag没被访问设为0，访问过设为1
Insert插入：如果T为空，在空的搜索树上插入第一个结点，赋值给T
如果T不为空，把这个V与根节点的V作比较，比根节点大就插入在右边，比根节点小就插入在左边

搜索树是否一样的判别

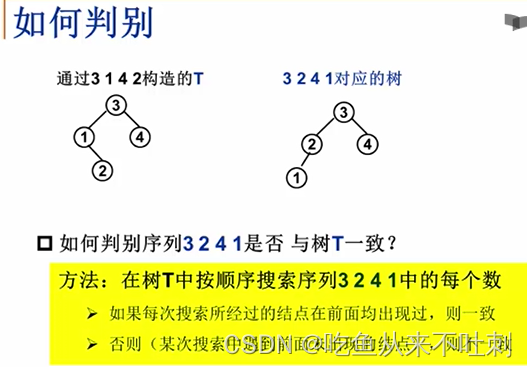
树是左边的树T，首先找3，3都在第一个找到了，flag标记为1
然后找2，查找顺序为3，1，2，其中3在前面碰到过了，1之前没碰到过，则可以断定3241和T是不一致的

查找代码

• 检查当前T里面查找整数V，在查找过程当中发现是不是一致的
  

• 首先判别，根节点flag是0还是1
• 若是flag=1，就说明查找过了，就去左边或者右边去找，看V与根节点值小v之间的关系，小的话去左边找，大的话去右边找，递归，如果相等，就意味着在这个序列里面有两个整数是出现了两次以上，重复出现了就认为是不一致的
• 若是flag=0，就意味着没被访问过，当前结点v是不是要查找的值，相等就把这个结点的flag设为1，返回1，就是原来没被找过，现在正好找这个结点，否则的话，当前节点flag=0，不是我找的，那就说明以前没见过，是不一致的，return 0

• 判别这N个元素的序列，每一个整数是不是一致的
  

• 读入第一个整数V，判别当前V与T的树根是不是一样的，若不一样就表明第一个元素对应的二叉树的树根与T的树根是不一样的，return 0
• 否则的话就说明树根是一样的，就把当前flag设为1
• 接下来逐个的进行check，循环1到n-1
  上述程序存在bug

改写之后为：

• 在发现有矛盾之后，就没必要check了，if预计就保证，若是矛盾了就直接读下一个整数
• flag=1的时候！flag=0，它是零的时候，后面check就不做了，当flag为0，就去做check，检查之后，如果return 0的话，意味着有矛盾了，flag=1，也就是flag=0，check返回值也为0的时候就刚刚发现了矛盾，这个时候就把flag设为1，所以这个循环就一直做，所以加flag的目的，就是发现有矛盾的时候让程序继续做，目的是为了把树读完
• 读完之后退出循环，flag=1 就说明发现矛盾了，就return 0，没发现矛盾就return 1，这样就能在发现不一致后还能将剩余的数运行完

清除标记与释放空间代码

源码

#include<stdio.h>
#include<stdlib.h>#define ElementType int
#define Null -1             //将Null定义为-1而不能是0，因为数组下标为0的地方仍保存有节点   
typedef struct TreeNode *Tree;
struct TreeNode {int v;ElementType flag;Tree Left,Right;
};
/*构造新结点*/
Tree NewNode(int V) {Tree T = (Tree)malloc(sizeof(struct TreeNode));T->v = V;T->Left = T->Right = NULL;T->flag = 0;return T;
}
/*插入结点*/
Tree Insert(Tree T, int V) {if (!T)T = NewNode(V);else {if (V > T->v)T->Right = Insert(T->Right, V);elseT->Left = Insert(T->Left,V);}return T;
}
/*构造新结点*/
Tree MakeTree(int N) {Tree T;int i, V;scanf("%d",&V);T = NewNode(V);for (i = 1; i < N; i++) {scanf("%d",&V);T = Insert(T,V);}return T;
}
/*查找结点*/
int check(Tree T, int V) {if (T->flag) {if (V < T->v) return check(T->Left,V);else if (V > T->v) return check(T->Right,V);else return 0;}else {if (V == T->v) {T->flag = 1;return 1;}else return 0;}
}/*判别这N个元素的序列，每一个整数是不是一致的*/
int Judge(Tree T, int N) {int i, V, flag = 0;/*flag:0代表目前还一致，1代表已经不一致*/scanf("%d",&V);if (V != T->v) flag = 1;else T->flag = 1;for (i = 1; i < N; i++) {scanf("%d",&V);if ((!flag) && (!check(T, V))) flag = 1;}if (flag)  return 0;else return 1;
}/*清除T中各结点的flag标记*/
void ResetT(Tree T) {if (T->Left) ResetT(T->Left);if (T->Right) ResetT(T->Right);T->flag = 0;
}
/*释放T的空间*/
void FreeTree(Tree T) {if (T->Left) FreeTree(T->Left);if (T->Right) FreeTree(T->Right);free(T);
}int main() {int N, L,i;Tree T;scanf("%d",&N);while (N) {scanf("%d",&L);T = MakeTree(N);for (i = 0; i < L; i++) {if (Judge(T, N))printf("Yes\n");else printf("No\n");ResetT(T);}FreeTree(T);scanf("%d",&N);}return 0;
}

运行

4 2
3 1 4 2
3 4 1 2
Yes
3 2 4 1
No
2 1
2 1
1 2
No
0