增强学习（二）——策略迭代与值迭代

本文主要是介绍增强学习（二）——策略迭代与值迭代，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在上一篇文章中，我主要介绍了马尔可夫决策过程（MDP）。在了解了增强学习的基本思想后，我们便可以继续讨论“最优策略”的求解方法：

我们之前已经说到了MDP可以表示成一个元组（X, A, P_sa, R），我们对最优策略的求解方法自然也就与这个元组密切相关：如果该过程的四元组均为已知，我们称这样的模型为“模型已知”，对这种已知所有环境因素的学习称为“有模型学习”（model-basedlearning）；与之对应的就是“无模型学习”，环境因素机器无法得知的，主要是指状态转移概率P_xa。

本篇博客对“有模型学习”的两种方法进行介绍，分别是策略迭代和值迭代。在此之前，我们需要明确增强学习的两大步骤，策略评估与策略改进：

策略评估：

在上一篇博客中，我们已经对“状态值函数”和“状态动作值函数”进行了简单介绍，但在之前的考虑中，我们是认为策略已知，故在贝尔曼方程中没有考虑策略π的取值与改进问题。我们在此以“状态值函数”和“状态动作值函数”的T步累积奖赏为例重新进行完整的推导：

    (1)

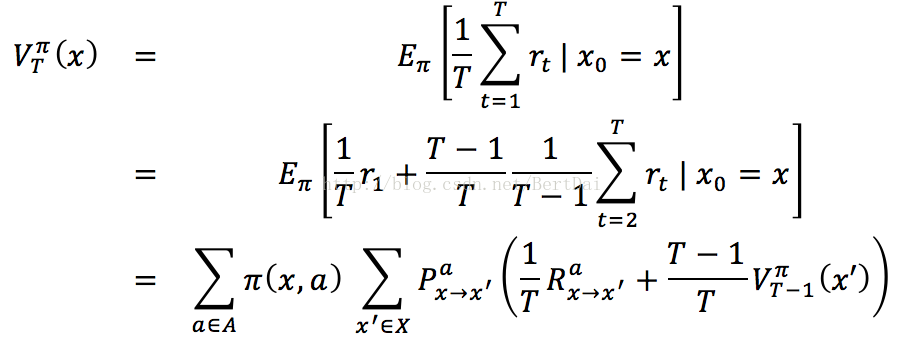
关于下标，R^a_x->x’表示的是在x状态下采取a动作，转移到x’状态后得到的回报，其他的类比即可。同理可以得到关于“状态动作值函数”Q的公式：

    (2)

这样的递归式才是对于完整的MDP四元组的贝尔曼等式。也就是说，我们通过这两个公式，就可以通过逐步递归的方式，在编程上实现对策略π的评估。伪代码如下：

策略改进：

由于我们已经知道了怎样对策略进行评估，那么，我们可以产生一个很直接的求解最优策略的方法：从一个初始化的策略出发，先进行策略评估，然后改进策略，评估改进的策略，再进一步改进策略……不断迭代更新，直达策略收敛，这种做法被称为“策略迭代”，伪代码如下：

其中，Q的计算是根据公式(2)来进行的。

此外，我们不难理解，当Q^π(x,π’(x))>=V^π(x)时，我们可以认为在x的状态下，π’策略相比原来的策略更好。再结合上一篇博文中的最优贝尔曼方程，我们可以将策略的改进视为值函数的改善，以此得出“值迭代”方法，伪代码如下：

但是，这两种方法的缺点显而易见：必须知道状态转移概率才能进行最优策略的计算。这在我们真实的使用场景中几乎不可能实现，所以，我们将在下一篇中介绍适用性更强的“无模型学习”。

这篇关于增强学习（二）——策略迭代与值迭代的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---