本文主要是介绍Unit2_1:动态规划DP,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 一、介绍
- 二、0-1背包问题
- 问题描述
- 分析
- 伪代码
- 时间复杂度
- 三、钢条切割问题
- 问题描述
- 分析
- 伪代码
- 过程
- 四、矩阵链乘法
- 背景
- 性质
- 分析
- 案例
- 伪代码
一、介绍
动态规划类似于分治法,它们都将一个问题划分为更小的子问题
最优子结构:问题的最优解包含子问题的最优解。DP适用的原因就在这
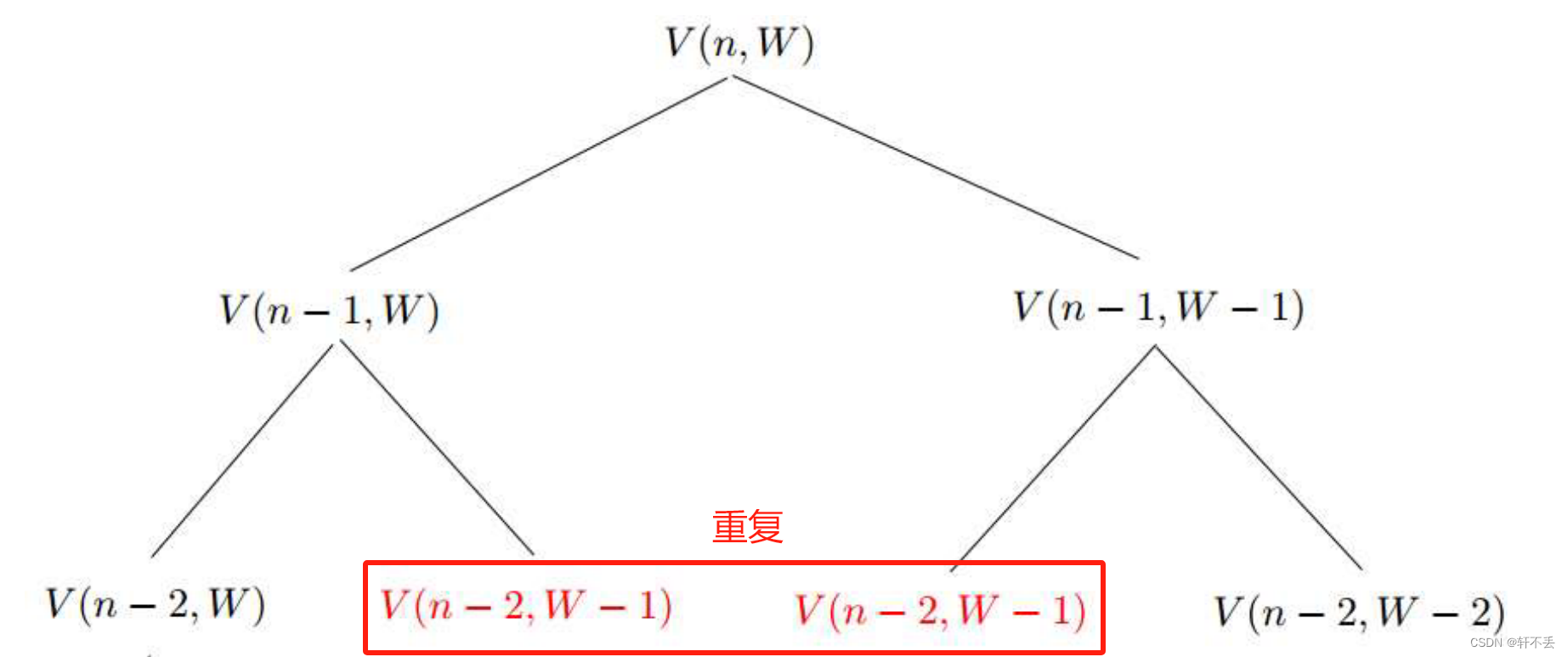
当子问题重叠时,即它们共享公共子问题时,可减小时间复杂度
DP通常用于优化问题,有许多解决方案的问题,我们想找到最好的一个
DP问题的求解思路一般就是
先描述最优解的结构
递归地定义最优解的值
计算最优解的值(通常是自下而上)
根据计算出的信息构造最优解(如果需要)
二、0-1背包问题
问题描述
n 个商品 , v i 表示第 i 个物品的价值 , w i 表示第 i 个物品的重量 一个能装入 W 重的背包 , 使用背包装下价值最多的物品 限制条件 : 我们不能取物品的一部分,我们取整个物品,或者什么都不取。 ( 这就是为什么它被称为 0 − 1 背包。 ) n个商品,v_i表示第i个物品的价值,w_i表示第i个物品的重量\\ 一个能装入W重的背包,使用背包装下价值最多的物品\\ 限制条件:我们不能取物品的一部分,我们取整个物品,或者什么都不取。\\(这就是为什么它被称为0-1背包。) n个商品,vi表示第i个物品的价值,wi表示第i个物品的重量一个能装入W重的背包,使用背包装下价值最多的物品限制条件:我们不能取物品的一部分,我们取整个物品,或者什么都不取。(这就是为什么它被称为0−1背包。)
分析
设 V [ i , w ] 表示重量为 w 背包 , 在前 i 种商品选择的最大价值 V[i,w]表示重量为w背包,在前i种商品选择的最大价值 V[i,w]表示重量为w背包,在前i种商品选择的最大价值
对于第i个物品,我们要么选取它,要么不选择,因此最大价值转移方程为
V [ i , w ] = m a x ( V [ i − 1 , w ] , v i + V [ i − 1 , w − w i ] ) V[i,w]=max(V[i-1,w],v_i+V[i-1,w-w_i]) V[i,w]=max(V[i−1,w],vi+V[i−1,w−wi])
若使用递归重复计算很多值,时间复杂度为 T ( n ) = O ( 2 W ) T(n)=O(2^W) T(n)=O(2W),因此要重复利用最优子结构的性质.
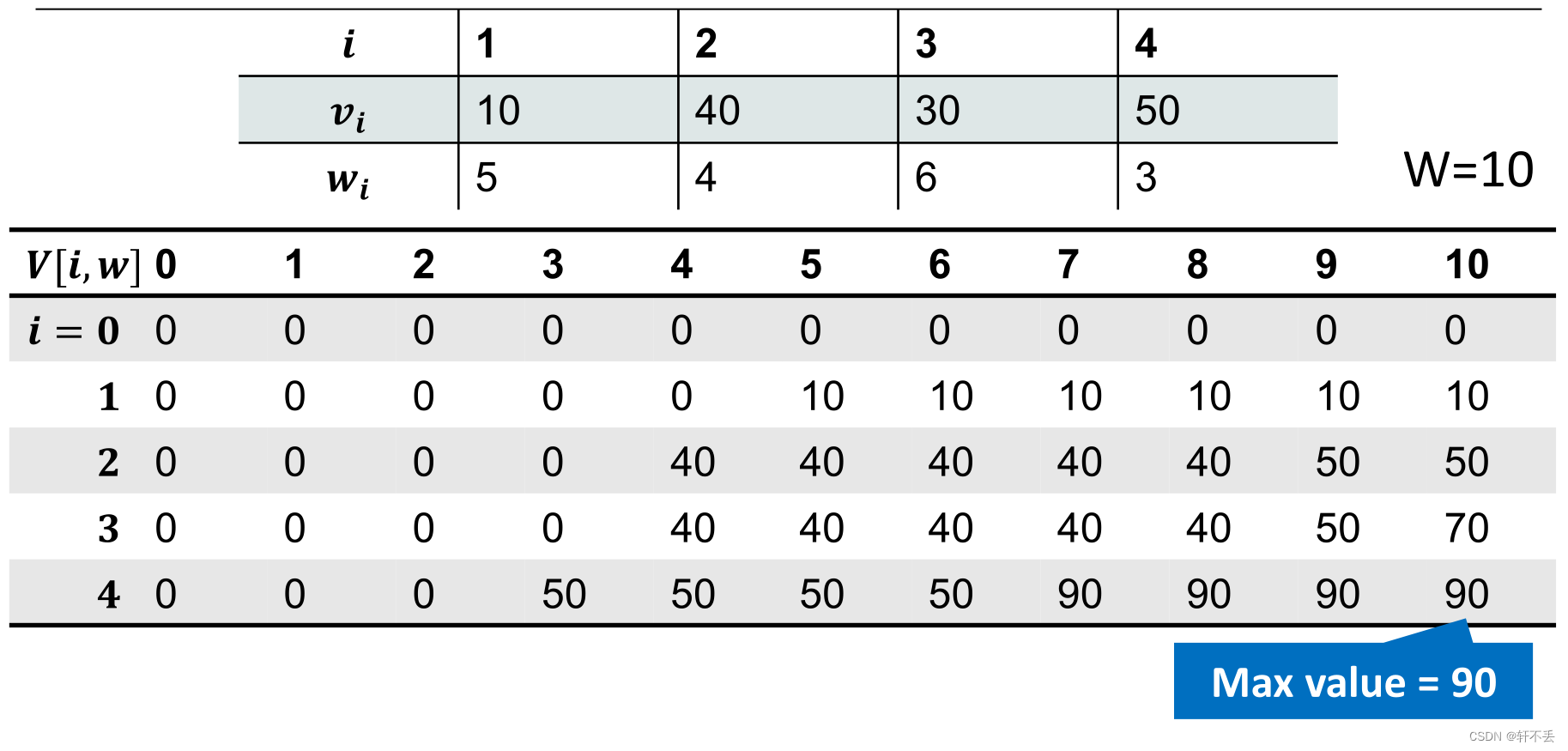
初始化: V [ 0 , w ] = 0 V[0,w]=0 V[0,w]=0 f o r for for 0 ≤ w ≤ W 0 \leq w \leq W 0≤w≤W 此时没有商品,自然没有价值
接下来按顺序填表:

伪代码
Knapsack(v,w,n,W)
for w=0 to W doV[0,w]=0;
end
for i=1 to n dofor w=0 to Wif w[i]<W thenV[i,w] = max{V[i-1,w],v[i]+V[i-1,w-w[i]]}elseV[i,w] = V[i-1,w]endend
end
return V[n,W]
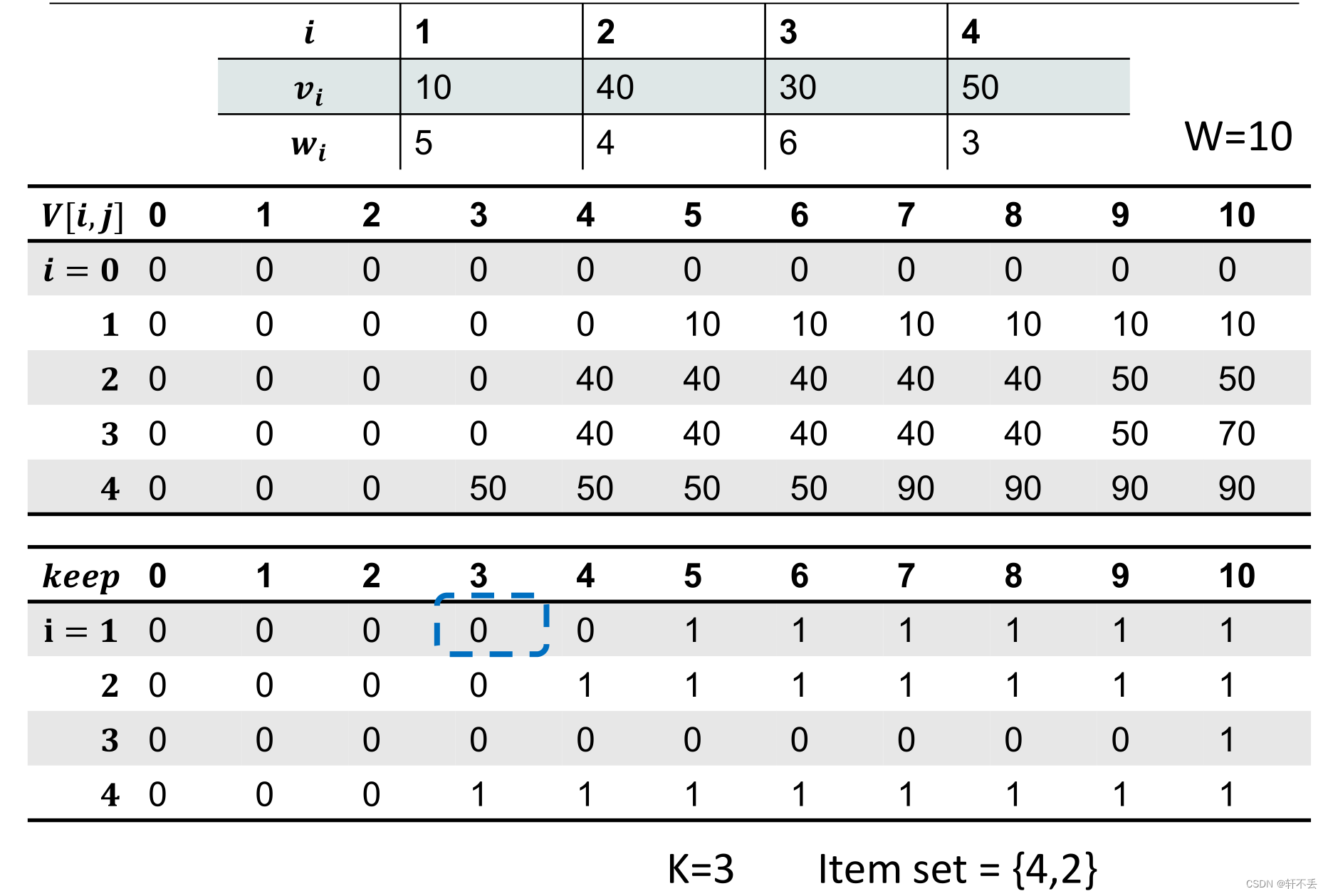
若是想要记录最优解的路径,需要维护一个 k e e p [ i ] [ w ] keep[i][w] keep[i][w],如果选择i作为 V [ i , w ] V[i,w] V[i,w],则 k e e p [ i ] [ w ] = 1 keep[i][w]=1 keep[i][w]=1
路径只需要
i f k e e p [ n , w ] = 1. 则选择 n 且继续从 k e p p [ n − 1 ] [ w − w n ] 开始 if keep[n,w]=1.则选择n且继续从kepp[n-1][w-w_n]开始 ifkeep[n,w]=1.则选择n且继续从kepp[n−1][w−wn]开始
i f k e e p [ n , w ] = 0. 则不选择 n 且继续从 k e p p [ n − 1 ] [ w ] 开始 if keep[n,w]=0.则不选择n且继续从kepp[n-1][w]开始 ifkeep[n,w]=0.则不选择n且继续从kepp[n−1][w]开始
因此路径输出代码:
K ← W
for i ← n to 1 doif keep[i][K] is equal to 1 thenOutput iK ← K-w[i]end
end
时间复杂度
两层循环,时间复杂度 T ( n ) = O ( n W ) T(n)=O(nW) T(n)=O(nW)
本质上,DP问题是用空间换时间,将结果放在空间中而不用下次花费时间再去计算
三、钢条切割问题
问题描述
给定一个长度为 n 的棒材和一个价格表,其中 p i 为长度为 i 的棒材的价格 确定最大的收入 r n , 以及切割钢条的方案 给定一个长度为n的棒材和一个价格表,其中pi为长度为i的棒材的价格\\ 确定最大的收入r_n,以及切割钢条的方案 给定一个长度为n的棒材和一个价格表,其中pi为长度为i的棒材的价格确定最大的收入rn,以及切割钢条的方案
分析
此题暴力解法,即遍历长度.每个点有两种选择,切 o r or or不切,判断哪种选择最合适即可,时间复杂度 T ( n ) = O ( 2 n ) T(n)=O(2^n) T(n)=O(2n).
考虑到最优子结构,可利用较短的杆最优收益来确定较长的,此题的状态转移如下:
r n = m a x ( p n , r 1 + r n − 1 , r 2 + r n − 2 , . . . . . , r n − 1 + r 1 ) r_n=max(p_n,r_1+r_{n-1},r_2+r_{n-2},.....,r_{n-1}+r_1) rn=max(pn,r1+rn−1,r2+rn−2,.....,rn−1+r1)
简化定义:
r n = m a x ( p i + r n − i ) r_n=max(p_i+r_{n-i}) rn=max(pi+rn−i) 1 ≤ i ≤ n 1 \leq i \leq n 1≤i≤n
伪代码
r[0] ← 0
for j ← 0 to n doq ← -∞for i ← 1 to j doq ← max(q,p[i]+r[j-i])endr[j] ← q if j != 0
end
return r[n]
这种做法时间复杂度 T ( n ) = O ( n 2 ) T(n)=O(n^2) T(n)=O(n2)
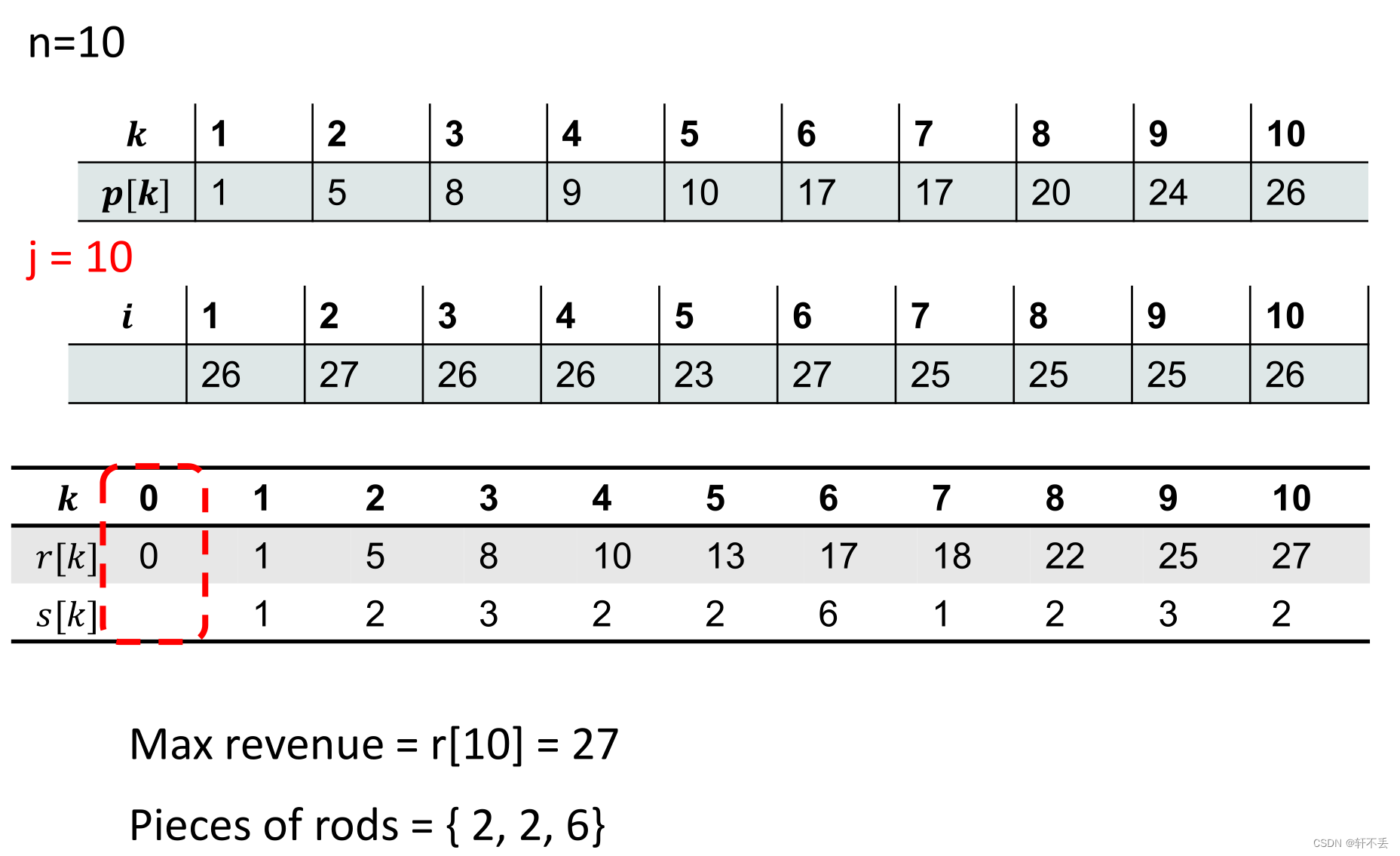
若是需要保存切割的方案,则需要维护一个 s [ n ] s[n] s[n]数组. s [ n ] 保存前一次切割的长度 s[n]保存前一次切割的长度 s[n]保存前一次切割的长度:
r[0] ← 0
for j ← 0 to n doq ← -∞for i ← 1 to j doif q < p[i]+r[j-i] thenq ← p[i]+r[j-i]s[j] ← iendendr[j] ← q if j != 0
end
while n>0 doOutput s[n]n ← n-s[n]
end
过程
四、矩阵链乘法
背景
p × q 矩阵 a 和 q × r 矩阵 B 的乘积 C = A B 是 p × r 矩阵 p × q矩阵a和q × r矩阵B的乘积C = AB是p × r矩阵 p×q矩阵a和q×r矩阵B的乘积C=AB是p×r矩阵
c [ i ] [ j ] = ∑ k = 1 q a [ i ] [ k ] b [ k ] [ j ] c[i][j]=\sum_{k=1}^{q}a[i][k]b[k][j] c[i][j]=∑k=1qa[i][k]b[k][j] f o r for for 1 ≤ i ≤ p 1 \leq i \leq p 1≤i≤p a n d and and 1 ≤ j ≤ r 1 \leq j \leq r 1≤j≤r
时间复杂度:注意 C C C有 p r pr pr个条目,每个条目需要 O ( q ) O(q) O(q)时间来计算,所以整个过程需要 O ( p q r ) O(pqr) O(pqr)时间
性质
矩阵乘法有结合律, A 1 A 2 A 3 = ( A 1 A 2 ) A 3 = A 1 ( A 2 A 3 ) A_1A_2A_3=(A_1A_2)A_3=A_1(A_2A_3) A1A2A3=(A1A2)A3=A1(A2A3)
因此当计算 A B C ABC ABC时,有两种选择, ( A B ) C = A ( B C ) (AB)C=A(BC) (AB)C=A(BC)
m u l t [ ( A B ) C ] = p q r + p r s mult[(AB)C]=pqr+prs mult[(AB)C]=pqr+prs
m u l t [ A ( B C ) ] = q r s + p q s mult[A(BC)]=qrs+pqs mult[A(BC)]=qrs+pqs
每种选择的时间复杂度不一样
因此矩阵链乘法需要解决的就是怎么样结合能使得计算的量最小
分析
令 A i . . j = A i A i + 1 . . . A j 令A_{i..j}=A_iA_{i+1}...A{j} 令Ai..j=AiAi+1...Aj,显然, A i . . j A_{i..j} Ai..j是 P i − 1 × P j P_{i-1}×P_j Pi−1×Pj的矩阵
A i . . j A_{i..j} Ai..j可以表示为 A i . . j = ( A i . . . A k ) ( A k + 1 . . . A j ) = A i . . k A k + 1.. j A_{i..j}=(A_i...A_k)(A_{k+1}...A{j})=A_{i..k}A_{k+1..j} Ai..j=(Ai...Ak)(Ak+1...Aj)=Ai..kAk+1..j
当 1 ≤ i ≤ j ≤ n 1 \leq i \leq j \leq n 1≤i≤j≤n时,令 m [ i , j ] m[i,j] m[i,j]表示计算 A i . . j A_{i..j} Ai..j所需的最小乘法次数。最优成本可以用下面的递归定义来描述
m ( i , j ) = { 0 i f i = j m i n i ≤ k ≤ j ( m ( i , k ) + m ( k + 1 , j ) + p i − 1 p k p j ) i f n = 1 m(i,j)=\left\{ \begin{array}{ll} 0 & if \space i=j \\ min_{i \leq k \leq j} (m(i,k)+m(k+1,j)+p_{i-1}p_kp_j)& if \space n=1 \nonumber \end{array} \right. m(i,j)={0mini≤k≤j(m(i,k)+m(k+1,j)+pi−1pkpj)if i=jif n=1
注意计算并保存 m [ i , j ] m[i, j] m[i,j]的顺序是,当计算 m [ i , j ] m[i, j] m[i,j]时, m [ i , k ] m[i, k] m[i,k]和 m [ k + 1 , j ] m[k + 1, j] m[k+1,j]的值已经可用,因此按矩阵链长度的递增顺序计算它们:
m [ 1 , 2 ] , m [ 2 , 3 ] , m [ 3 , 4 ] , … , m [ n − 3 , n − 2 ] , m [ n − 2 , n − 1 ] , m [ n − 1 , n ] m[1,2], m[2,3], m[3,4],…, m[n-3,n-2], m[n-2,n-1], m[n-1,n] m[1,2],m[2,3],m[3,4],…,m[n−3,n−2],m[n−2,n−1],m[n−1,n]
m [ 1 , 3 ] , m [ 2 , 4 ] , m [ 3 , 5 ] , … , m [ n − 3 , n − 1 ] , m [ n − 2 , n ] m[1,3], m[2,4], m[3,5],…, m[n-3,n-1], m[n-2,n] m[1,3],m[2,4],m[3,5],…,m[n−3,n−1],m[n−2,n]
m [ 1 , 4 ] , m [ 2 , 5 ] , m [ 3 , 6 ] , … , m [ n − 3 , n ] m[1,4], m[2,5], m[3,6],…, m[n-3,n] m[1,4],m[2,5],m[3,6],…,m[n−3,n]
… … …
m [ 1 , n − 1 ] , m [ 2 , n ] m[1,n-1], m[2,n] m[1,n−1],m[2,n]
m [ 1 , n ] m[1,n] m[1,n]
若需要记录分隔括号路径,需要维护一个二维数组 s [ 1.. n , 1.. n ] s[1..n, 1..n] s[1..n,1..n],里面存储 A i . . j A_{i..j} Ai..j的最优分隔k
s [ 1 , n ] s[1,n] s[1,n] ( A 1 . . A s [ 1 , n ] ) ( A s [ 1 , n ] + 1 . . . A n ) (A_1..A_{s[1,n]})(A_{s[1,n]+1}...A{n}) (A1..As[1,n])(As[1,n]+1...An)
s [ 1 , s [ 1. n ] ] s[1,s[1.n]] s[1,s[1.n]] ( A 1 . . A s [ 1 , s [ 1. n ] ] ) ( A s [ 1 , s [ 1. n ] ] + 1 . . . A n ) (A_1..A_{s[1,s[1.n]]})(A_{s[1,s[1.n]]+1}...A{n}) (A1..As[1,s[1.n]])(As[1,s[1.n]]+1...An)
案例
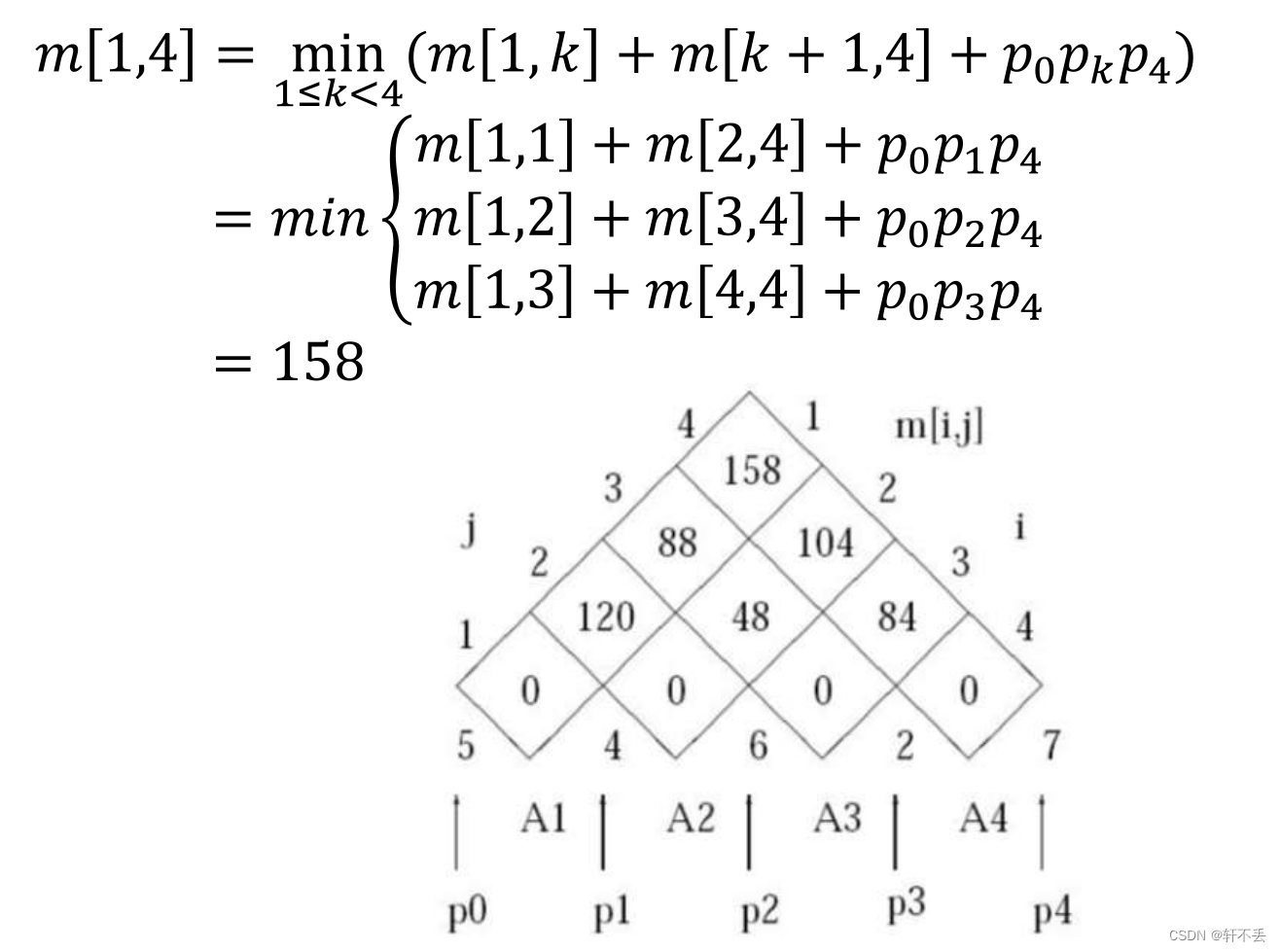
伪代码
MatrixChain(p,n)
for i ← 1 to n dom[i,i] ← 0;
end
for l ← 2 to n dofor i ← 1 to n-l+1 doj ← i+l-1;m[i,j] ← ∞for k ← i to j-1 doq ← m[i,k]+m[k+1,j]+p[i-1]*p[k]*p[j]if q<m[i,j] thenm[i,j] ← qs[i,j] ← kendendend
end
return m[1,n] and s
三层循环,时间复杂度 T ( n ) = O ( n 3 ) T(n)=O(n^3) T(n)=O(n3)
这篇关于Unit2_1:动态规划DP的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







