本文主要是介绍FPT:又是借鉴Transformer,这次多方向融合特征金字塔 | ECCV 2020,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
论文提出用于特征金字塔的高效特征交互方法FPT,包含3种精心设计的特征增强操作,分别用于借鉴层内特征进行增强、借鉴高层特征进行增强以及借鉴低层特征进行增强,FPT的输出维度与输入一致,能够自由嵌入到各种包含特征金字塔的检测算法中,从实验结果来看,效果不错
来源:晓飞的算法工程笔记 公众号
论文: Feature Pyramid Transformer

- 论文地址:https://arxiv.org/abs/2007.09451
- 论文代码:https://github.com/ZHANGDONG-NJUST/FPT
Introduction
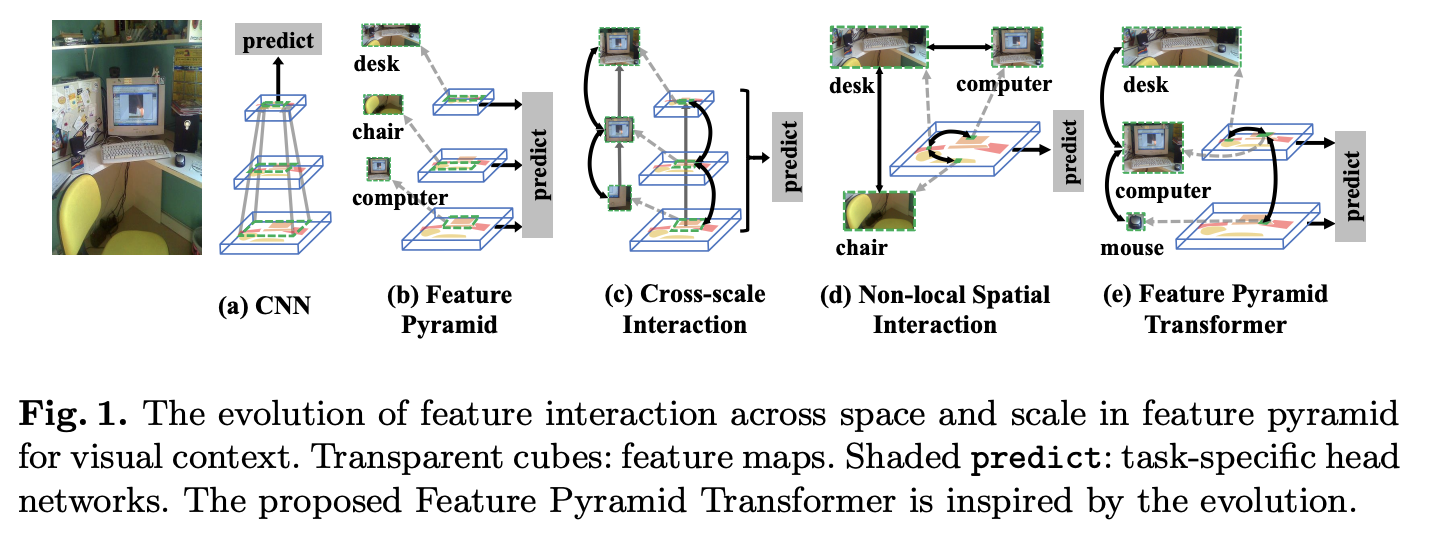
讲论文前先捋一下CNN网络结构相关的知识,论文的思想主要来自两个,一个是特征金字塔结构,一个是Non-local网络:
- 首先是特征金字塔,如图1a,CNN网络以层级结构的形式逐层提取更丰富的特征,然后使用最后的特征层进行预测。但对于一些小物体而言,最后一层的特征图往往没有足够的像素点进行预测。为了更好地对不同大小的物体进行预测,人们提出图1b的金字塔特征,大物体使用高层的粗粒度特征,小物体使用底层的细粒度特征。对于一些pixel-level任务,比如语义分割,需要综合不同层的上下文信息进行细致的预测,所以就需要图1c的预测结构。
- 其次是Non-local network,该网络借鉴了NLP模型的Self-attention思想,如图1d所示,能够借鉴特征图上的其它特征点来对当前特征点进行增强。
基于上面两个思想,论文提出了FPT(Feature Pyramid Transformer),结构如图1e所示,核心在特征金字塔上进行类似Non-local的特征增强,然后再使用多层特征进行预测。FPT设计了3种特征增强操作,也是论文的主要贡献:
- ST(Self-Transformer):跟non-local操作一样在对当前层进行特征增强。
- GT(Grounding Transformer):这是top-down形式的non-local操作,将高层特征(尺寸小的)分别用于低层特征的增强。
- RT(Rendering Transformer):这是bottom-up形式的non-local操作,将低层特征(尺寸大的)分别用于高层特征的增强。
Feature Pyramid Transformer

FPT的特征转换流程如图2所示,输入为金字塔特征,首先对每层特征分别进行ST、GT、RT特征增强得到多个增强后的特征,然后对增强的特征按尺寸进行排序,将相同大小的特征concate到一起,通过卷积将增强后的特征维度恢复到输入时的相同维度。
Non-Local Interaction Revisited
由于论文提出的特征增强操作与non-local操作有很大关系,这里需要先介绍下non-local的思想。常规non-local操作的输入为单特征图 X X X上的queries(Q), keys(K)和values(V),输出与 X X X尺寸相同的增强特征 X ^ \hat{X} X^:

q i = f q ( X i ) ∈ Q q_i=f_q(X_i)\in Q qi=fq(Xi)∈Q, k j = f k ( X j ) ∈ K k_j=f_k(X_j)\in K kj=fk(Xj)∈K, v j = f v ( X j ) ∈ V v_j=f_v(X_j)\in V vj=fv(Xj)∈V, f q ( ⋅ ) f_q(\cdot) fq(⋅)、 f k ( ⋅ ) f_k(\cdot) fk(⋅)和 f v ( ⋅ ) f_v(\cdot) fv(⋅)为对应的线性变换, X i X_i Xi和 X j X_j Xj为特征图 X X X上的第 i t h i^{th} ith和 j t h j^{th} jth位置上的特征, F s i m F_{sim} Fsim为相似度函数,默认为点积, F n o m F_{nom} Fnom为归一化函数,默认为softmax, F m u l F_{mul} Fmul为权重集成函数,默认为矩阵相乘, X ^ i \hat{X}_i X^i为输出特征图 X ^ \hat{X} X^的第 i t h i^{th} ith位置上的特征。
Self-Transformer
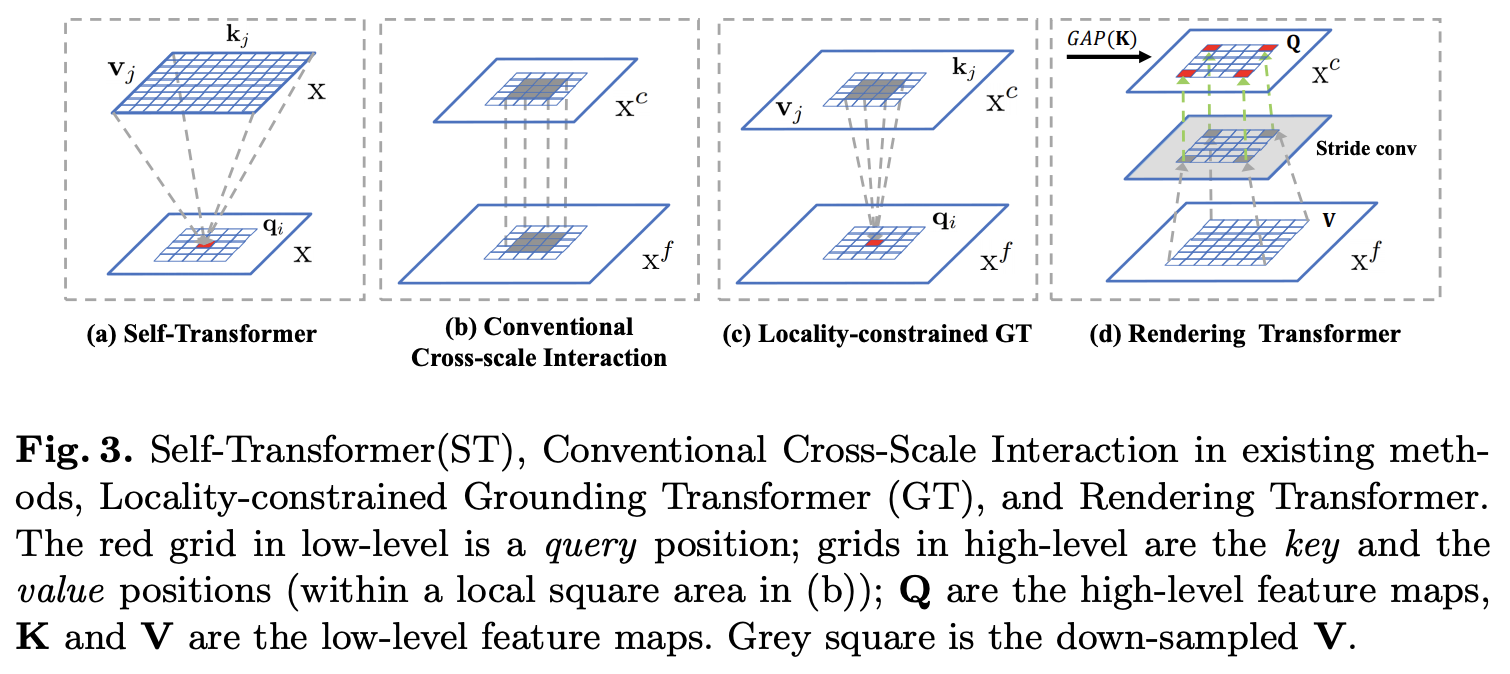
ST为改进版non-local操作,如图1a所示,主要有两点不同:
- 将 q i q_i qi和 k j k_j kj分为 N \mathcal{N} N部分,然后计算每部分的每组 q i , n q_{i,n} qi,n和 k j , n k_{j,n} kj,n相似度分数 s i , j n s^n_{i,j} si,jn
- 相似度计算使用改进的MoS(Mixture of Softmaxes)函数 F m o s F_{mos} Fmos:
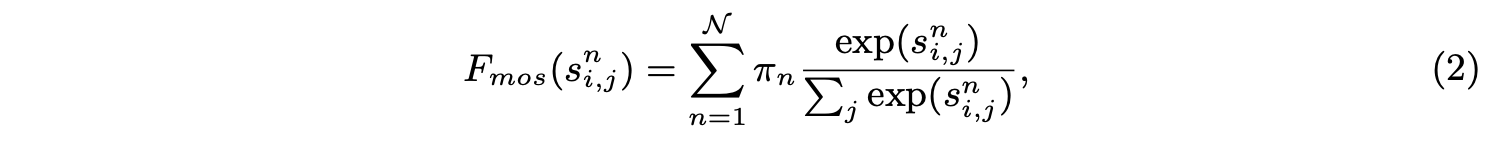
π n = S o f t m a x ( w n T k ‾ ) \pi_n=Softmax(w^T_n \overline{k}) πn=Softmax(wnTk)为特征集成时的权重, w n w_n wn为可学习的线性变换, k ‾ \overline{k} k为所有 k j k_j kj的均值。
基于上述的改进,ST定义为:
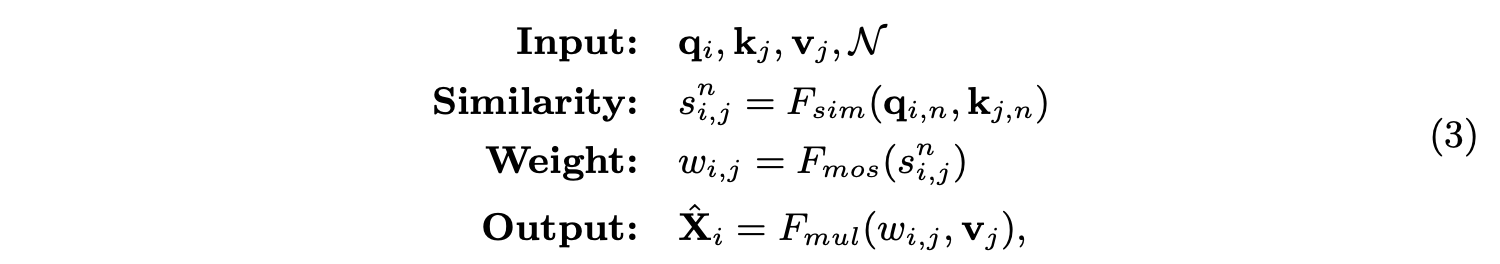
Grounding Transformer
GT是top-down形式的non-local操作,如图2c所示,借用高层的粗粒度特征 X c X^c Xc来增强低层的细粒度特征 X f X^f Xf。在计算时,相似度计算由点积替换为更高效的欧氏距离 F e u d F_{eud} Feud:
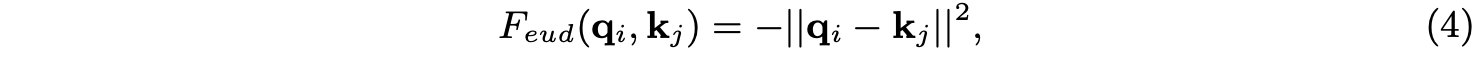
q i = f q ( X i f ) q_i=f_q(X^f_i) qi=fq(Xif), k j = f k ( X j c ) k_j=f_k(X^c_j) kj=fk(Xjc)。GT跟ST一样将 q i q_i qi和 k j k_j kj分为 N \mathcal{N} N部分,完整的定义为:
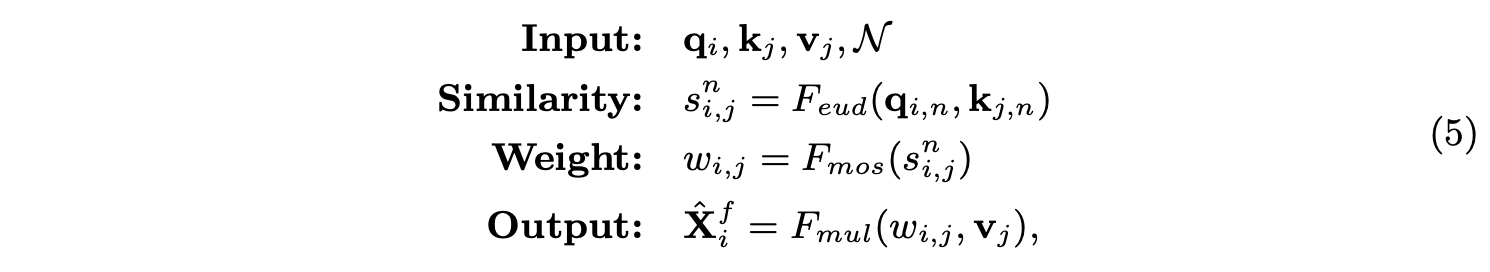
在特征金字塔中,高低层特征分别包含图片的全局和局部信息,而对于语义分割任务,不需要关注过多高层的全局信息,更多的是需要query位置附近的上下文信息,所以图3b的跨层卷积对语义分割任务十分有效。由于GT操作是全局计算,所以论文提出了局部约束(Locality-constrained)的GT操作LGT,如图3c所示,每个 q i q_i qi只与高层局部区域的 k j k_j kj和 v j v_j vj进行计算。高层局部区域以 q i q_i qi对应的位置为中心,边长(square size)为固定值。如果高层的局部区域越出了特征图,则使用0代替。
Rendering Transformer
与GT相反,RT是bottom-up形式的non-local操作,借用低层的细粒度特征来增强高层的粗粒度特征。RT也是局部约束(Locality-constrained)的,以channel-wise进行计算的,定义高层特征为 Q Q Q,低层特征为 K K K和 V V V,计算步骤包含如下:
- 对 K K K和进行全局平均池化得到权重 w w w。
- 使用权重 w w w对 Q Q Q进行加权得到 Q a t t Q_{att} Qatt。
- 对 V V V进行带stride的 3 × 3 3\times 3 3×3卷积下采样得到 V d o w V_{dow} Vdow。
- 使用 3 × 3 3\times 3 3×3卷积对 Q a t t Q_{att} Qatt进行调整,并与 V d o w V_{dow} Vdow相加,再过一层 3 × 3 3\times 3 3×3卷积后输出。
完整RT的定义为:

F a t t ( ⋅ ) F_{att}(\cdot) Fatt(⋅)为外积函数, F s c o v ( ⋅ ) F_{scov}(\cdot) Fscov(⋅)为带stride的 3 × 3 3\times 3 3×3卷积, F c o n v ( ⋅ ) F_{conv}(\cdot) Fconv(⋅)为用于调整的 3 × 3 3\times 3 3×3卷积, F a d d ( ⋅ ) F_{add}(\cdot) Fadd(⋅)为包含 3 × 3 3\times 3 3×3卷积的特征相加函数。
Experiments
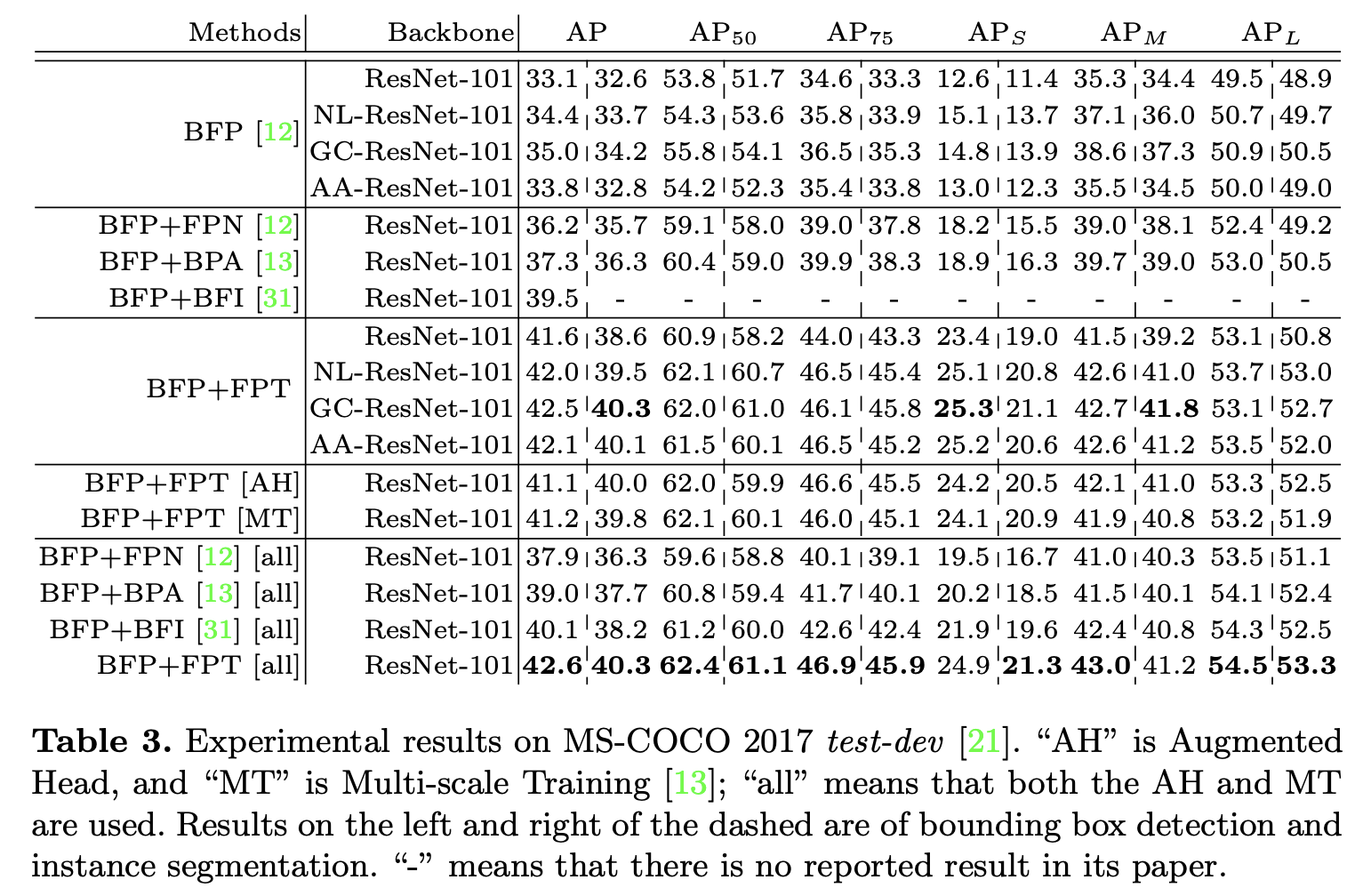
在COCO上与其它算法的对比实验。
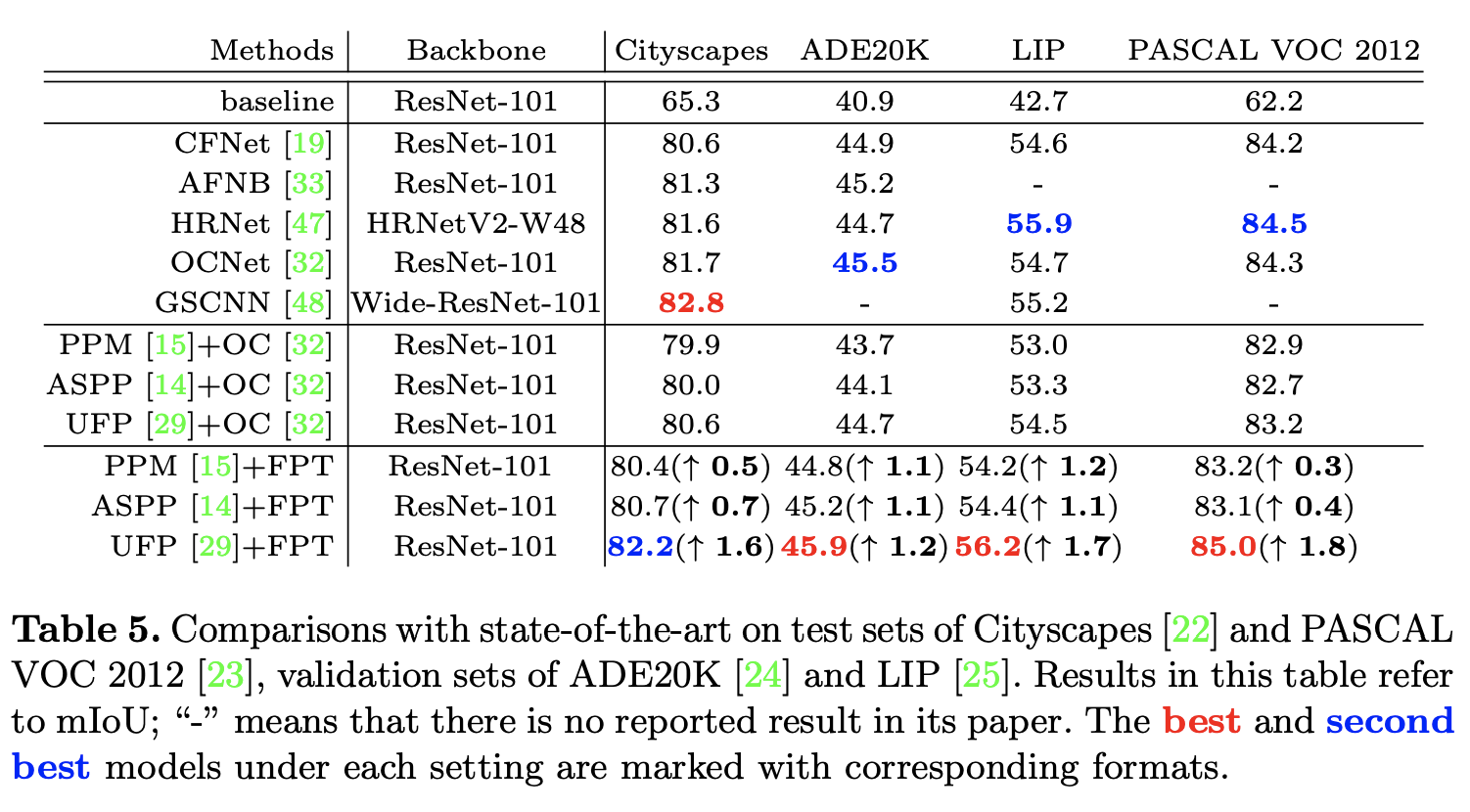
在多个数据集上的进行语义分割性能对比。
Conclusion
论文提出用于特征金字塔的高效特征交互方法FPT,包含3种精心设计的特征增强操作,分别用于借鉴层内特征进行增强、借鉴高层特征进行增强以及借鉴低层特征进行增强,FPT的输出维度与输入一致,能够自由嵌入到各种包含特征金字塔的检测算法中,从实验结果来看,效果不错。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】

这篇关于FPT:又是借鉴Transformer,这次多方向融合特征金字塔 | ECCV 2020的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





