【梳理】离散数学 第16章 树 16.1 无向树及其性质 16.2 生成树 16.3 根树及其应用

教材：《离散数学》第2版 屈婉玲 耿素云 张立昂 高等教育出版社
源文档高清截图在最后

第16章 树

16.1 无向树及其性质

1、连通而无回路的无向图叫做无向树，简称树。每个连通分量都是树的无向图称作森林。平凡图也成平凡树。在无向树中，悬挂顶点（度数为1的顶点）称树叶，度数大于等于2的顶点称作分支点。

2、树的充分必要条件：
设G(V, E)是n阶m条边的无向图，则下列命题等价：
【1】G是树。
【2】G中任意两个顶点之间存在唯一的路径。
【3】G无回路，且m = n – 1。
【4】G是连通的，且m = n – 1。
【5】G是连通的，且任何边均为桥。
【6】G中没有回路，但任何两个不同的顶点之间添加新的边后能产生唯一一个含新边的圈。
证明 【1】推【2】：由G的连通性以及“n阶图G中，如存在v到自身的回路，则一定存在v到自身的长度小于等于n的初级回路”可知，对任意的u，v∈V，u到v存在一条路径。若路径不是唯一的，设Γ1和Γ2都是u到v的路径，则Γ1和Γ2上的边就可以构成回路。这与树的定义矛盾。
【2】推【3】。首先证明G中无回路。若G存在关联某顶点v的环，则v到v存在长度为0和1的两条路径（初级回路是路径的特殊情况；顶点到自身都具有长度为0的一条路径），与已知矛盾。若G存在长度≥2的圈，则圈上任何两个顶点之间都存在两条不同的路径，也引起矛盾。
然后归纳证明m = n – 1。当n = 1时G为平凡图，结论成立。设n≤k时结论都成立，那么n = k + 1时结论也要成立。此时，设e = (u, v)为G的一条边，由于G无回路，所以u到v只有唯一的路径（否则任意两条路径均可形成回路），所以G – e为两个连通分量G1、G2。设ni，mi分别为Gi中的顶点数和边数，则显然ni≤k。由归纳假设，mi = ni – 1，i = 1，2。于是m = m1 + m2 + 1 = n1 + n2 – 2 + 1 = n – 1。得证。
【3】推【4】。只要证明G是连通的（注意：一个图是树，是该图连通且无回路的必要条件，现在证前者是后者的充分条件）。假设G不连通，则设G由s个连通分量G1，G2，……，Gs（s≥2）。又每个Gi均无回路，因此Gi都是树。由前面的证明，mi = ni – 1，于是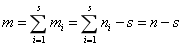 。但s≥2，这与m = n – 1矛盾。
【4】推【5】。只要证G中每条边均为桥。对任意的e∈E，均有 |E(G – e)| = n – 1 – 1 = n – 2。由第14章习题50，G – e不是连通图，故e为桥。
【5】推【6】。由于G的每条边均为桥，因此G中无圈。（在圈中删掉任意一条边都不影响圈上任意两点的连通性）又由于G连通，所以G为树。所以G中任意两个不同顶点u，v之间存在唯一的路径Γ。设e是在u，v之间添加的新边，则Γ∪e是一个圈，且显然是唯一的。
【6】推【1】。根据树的定义，只要证明G是连通的。对任意两个不同顶点u和v，在u，v之间添加一条新边e，产生唯一的一个含e的圈C。显然C – e为G中u到v的通路，故u ~ v。而u，v是任意选定的，所以G是连通的。

3、设T是