[Unity]硬表面模型描边断裂问题解决过程记录

在Shader中使用单独一个Pass渲染轮廓线是非常常见的做法，其原理是在该Pass的顶点着色器中将模型顶点加上沿法线方向的偏移是原本的模型扩大一圈并剔除正向面，从而实现轮廓线效果。
但是使用该方法有一个要求就是模型的法线必须连续，也就是模型必须光滑表面，如果是硬表面的模型，由于转折处法线不连贯，会导致沿法线扩大的轮廓线模型断裂，如下图：

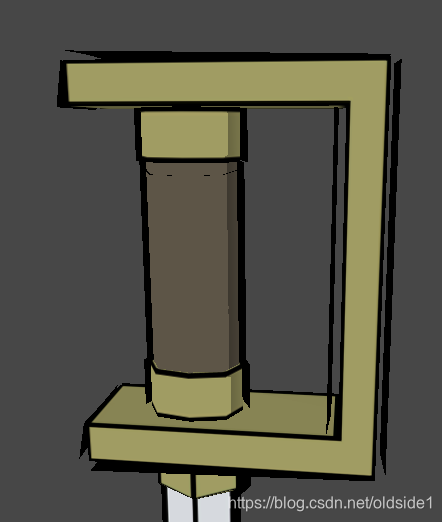
原因是转折处法线不连贯：

解决方案有二，但思路是一样的，就是将一个点光滑处理后的法线值存入该点的顶点色的RGB通道中，A通道可以用来控制轮廓线的粗细。需要注意的是，存入顶点色的法线必须是切线空间下的坐标，如果是模型空间下的坐标的话，一旦模型需要做动画，模型的轮廓线就会计算错误。一开始想要在3dsMax中通过脚本实现以上思路，结果发现Max脚本只能设置“控制点”的颜色，而不能分开设置同一顶点但是不同“Ploygon顶点”的颜色（不知道怎样描述），反正我是看了半天Max文档也没找到方法，如果有方法的话希望大佬能够在评论区告知，万分感谢！下面说一下我实验成功的两种解决方案。

（本人程序菜鸡，只会点基础，代码烂的一批，轻喷）
更新：才知道还有个“资产后处理（AssetPostprocessor）”这么个东西，感觉不错，可以看看这位大佬的文章：【Job/Toon Shading Workflow】自动生成硬表面模型Outline Normal
方案一：在Unity中实现以上思路，并将处理好的模型存为新的.asset文件（一开始我还以为获取模型的时候使用GetComponent<SkinnedMeshRenderer>().sharedMesh然后编辑该mesh就能就改资源文件，结果发现理解错了，这样并不行，而且Unity也不能保存Mesh为Fbx，只能存为.asset文件 ）。具体实现为，Unity中新建SetNormalsInVertColor脚本，脚本内容如下：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEditor;public class SetNormalsInVertColor : MonoBehaviour
{public string NewMeshPath = "Assets/";void Awake(){//获取MeshMesh mesh = new Mesh();if (GetComponent<SkinnedMeshRenderer>()){mesh = GetComponent<SkinnedMeshRenderer>().sharedMesh;}if (GetComponent<MeshFilter>()){mesh = GetComponent<MeshFilter>().sharedMesh;}Debug.Log(mesh.name);//声明一个Vector3数组，长度与mesh.normals一样，用于存放//与mesh.vertices中顶点一一对应的光滑处理后的法线值Vector3[] meshNormals = new Vector3[mesh.normals.Length];//开始一个循环，循环的次数 = mesh.normals.Length = mesh.vertices.Length = meshNormals.Lengthfor (int i = 0; i < meshNormals.Length; i++){//定义一个零值法线Vector3 Normal = new Vector3(0,0,0);//遍历mesh.vertices数组，如果遍历到的值与当前序号顶点值相同，则将其对应的法线与Normal相加for (int j = 0; j < meshNormals.Length; j++){if (mesh.vertices[j] == mesh.vertices[i]){Normal += mesh.normals[j];}}//归一化Normal并将meshNormals数列对应位置赋值为Normal,到此序号为i的顶点的对应法线光滑处理完成//此时求得的法线为模型空间下的法线Normal.Normalize();meshNormals[i] = Normal;}//构建模型空间→切线空间的转换矩阵ArrayList OtoTMatrixs = new ArrayList();for (int i = 0; i < mesh.normals.Length; i++){Vector3[] OtoTMatrix = new Vector3[3];OtoTMatrix[0] = new Vector3(mesh.tangents[i].x, mesh.tangents[i].y, mesh.tangents[i].z);OtoTMatrix[1] = Vector3.Cross(mesh.normals[i], OtoTMatrix[0]);OtoTMatrix[1] = new Vector3(OtoTMatrix[1].x * mesh.tangents[i].w, OtoTMatrix[1].y * mesh.tangents[i].w, OtoTMatrix[1].z * mesh.tangents[i].w);OtoTMatrix[2] = mesh.normals[i];OtoTMatrixs.Add(OtoTMatrix);}//将meshNormals数组中的法线值一一与矩阵相乘，求得切线空间下的法线值for (int i = 0; i < meshNormals.Length; i++){Vector3 tNormal;tNormal = Vector3.zero;tNormal.x = Vector3.Dot(((Vector3[])OtoTMatrixs[i])[0], meshNormals[i]);tNormal.y = Vector3.Dot(((Vector3[])OtoTMatrixs[i])[1], meshNormals[i]);tNormal.z = Vector3.Dot(((Vector3[])OtoTMatrixs[i])[2], meshNormals[i]);meshNormals[i] = tNormal;}//新建一个颜色数组把光滑处理后的法线值存入其中Color[] meshColors = new Color[mesh.colors.Length];for (int i = 0; i < meshColors.Length; i++){meshColors[i].r = meshNormals[i].x * 0.5f + 0.5f;meshColors[i].g = meshNormals[i].y * 0.5f + 0.5f;meshColors[i].b = meshNormals[i].z * 0.5f + 0.5f;meshColors[i].a = mesh.colors[i].a ;}//新建一个mesh，将之前mesh的所有信息copy过去Mesh newMesh = new Mesh();newMesh.vertices = mesh.vertices;newMesh.triangles = mesh.triangles;newMesh.normals = mesh.normals;newMesh.tangents = mesh.tangents;newMesh.uv = mesh.uv;newMesh.uv2 = mesh.uv2;newMesh.uv3 = mesh.uv3;newMesh.uv4 = mesh.uv4;newMesh.uv5 = mesh.uv5;newMesh.uv6 = mesh.uv6;newMesh.uv7 = mesh.uv7;newMesh.uv8 = mesh.uv8;//将新模型的颜色赋值为计算好的颜色newMesh.colors = meshColors;newMesh.colors32 = mesh.colors32;newMesh.bounds = mesh.bounds;newMesh.indexFormat = mesh.indexFormat;newMesh.bindposes = mesh.bindposes;newMesh.boneWeights = mesh.boneWeights;//将新mesh保存为.asset文件，路径可以是"Assets/Character/Shader/VertexColorTest/TestMesh2.asset"                          AssetDatabase.CreateAsset( newMesh, NewMeshPath);AssetDatabase.SaveAssets();Debug.Log("Done");}
}

然后将该脚本挂载到要处理的模型上面，play一下就行了，新模型就会出现在设置好的路径下。必须要说的是，需要处理的模型本身必须要有顶点色通道，也就是说在模型软件导出时必须要设置过顶点色，要不然导出的模型没有顶点色通道，当然即便没有顶点色通道在脚本中也可以处理，但是我懒得研究了ε=(´ο｀*)))

方案二：由于在Unity中无法对fbx资源进行修改，这就使得整个资源导入的流程不够流畅。于是我决定研究一下Fbx SDK，用C++写个小程序直接对Fbx文件进行操作，操作的内容与方案一完全一样：计算法线→空间转换→写入顶点色→导出文件。需要处理的模型本身必须要有顶点色通道，也就是说在模型软件导出时必须要设置过顶点色，否则导出的模型没有顶点色通道，当然即便没有顶点色通道在脚本中也可以处理，但是我懒得研究了ε=(´ο｀*)))
按照Fbx sdk的文档所示，下载配置好sdk，代码如下：

#include "pch.h"
#include <iostream>
#include <fbxsdk.h>void StoreNormalsToVertColor(FbxNode* node) 
{if (node->GetChildCount()){for (int i = 0; i < node->GetChildCount(); i++){if (node->GetChild(i)->GetMesh()){//获取meshFbxMesh* mesh = node->GetChild(i)->GetMesh();//获取layer，顶点色、法切线之类的顶点信息几乎存在layer中FbxLayer* layer0 = mesh->GetLayer(0);//依次获取layer中的顶点色层、法线层、切线层、副法线（或者叫副切线）层FbxLayerElementVertexColor* VertColor = layer0->GetVertexColors();FbxLayerElementNormal* VertNormal = layer0->GetNormals();FbxLayerElementTangent* VertTangent = layer0->GetTangents();FbxLayerElementBinormal* VertBinomral = layer0->GetBinormals();//逐顶点遍历操作for (int j = 0; j < mesh->GetPolygonVertexCount(); j++){//声明一个整型数组，用于存放与当前遍历顶点同属一个控制点的顶点序列//数组用的是FbxSdk内置的数组，是动态数组，比较好使FbxArray<int> SameControlPointsIndex;for (int k = 0; k < mesh->GetPolygonVertexCount(); k++){if (mesh->GetPolygonVertices()[k] == mesh->GetPolygonVertices()[j]){SameControlPointsIndex.Add(k);}}//声明一个Vector4数组，获取并存放上面声明的顶点序列数组中所有不同方向的法线//需要注意的是，与Unity的顶点不同，这里的顶点中有很多法线的方向是重复的//如果将重复的法线也参与计算则算出来的值是错误的，轮廓线会扭曲，说出来都是泪//所以使用AddUnique保证去掉重复的法线方向FbxArray<FbxVector4> Normals;for (int x = 0; x < SameControlPointsIndex.Size(); x++){FbxVector4 Normal = VertNormal->GetDirectArray()[SameControlPointsIndex[x]];Normals.AddUnique(Normal);}//将所有不同方向的法线加在一起并归一化获得光滑法线FbxVector4 SmoothNormal;for (int n = 0; n < Normals.Size(); n++){SmoothNormal += Normals[n];}SmoothNormal.Normalize();//分别获取当前顶点的切线、法线、副切线用于构建模型→切线空间的转换矩阵//需要注意的是：法线、切线、副切线的映射方式（也就是存储方式）是与顶点//序列一一对应，所以直接GetDirectArray()[顶点序号]就可以FbxVector4 Tangent = VertTangent->GetDirectArray()[j];FbxVector4 Normal = VertNormal->GetDirectArray()[j];FbxVector4 Bitangent = VertBinomral->GetDirectArray()[j];//将法线从模型空间转为切线空间//FbxSdk的内置矩阵类型不会使，算出来的值有问题，所以还是手动计算FbxVector4 tmpVector;tmpVector = SmoothNormal;tmpVector[0] = Tangent.DotProduct(SmoothNormal);tmpVector[1] = Bitangent.DotProduct(SmoothNormal);tmpVector[2] = Normal.DotProduct(SmoothNormal);tmpVector[3] = 0;SmoothNormal = tmpVector;//获取当前顶点的颜色信息存放于其layer中的序号//与法切副不同，顶点色数据在layer中的存储方式（映射Mapping方式）稍微复杂//首先要使用GetIndexArray()[顶点序号]获取其颜色值在DirectArray中的序号//然后使用GetDirectArray()[获得的序号]来获得该顶点的顶点色信息int VertColorIndex = VertColor->GetIndexArray()[j];//声明一个颜色值，将法线数值范围从-1~1处理为0~1后存入RGB通道中，A通道保持//不变，因为其中存放着轮廓线大小信息FbxColor Color;Color.mRed = SmoothNormal[0] * 0.5f + 0.5f;Color.mGreen = SmoothNormal[1] * 0.5f + 0.5f;Color.mBlue = SmoothNormal[2] * 0.5f + 0.5f;Color.mAlpha = VertColor->GetDirectArray()[VertColorIndex].mAlpha;//将颜色写入顶点颜色layer中VertColor->GetDirectArray().SetAt(VertColorIndex, Color);}}//递归调用，确保场景中所有mesh都得到处理StoreNormalsToVertColor(node->GetChild(i));}}
}int main(int argc, char** argv) {// lFilename是输入路径，lFilename2是输出路径const char* lFilename = "Weapon.fbx";const char* lFilename2 = "Export.fbx";//主函数中几乎都是FbxSdk文档中所写的代码，是导入导出fbx所需要的的标准流程// Initialize the SDK manager. This object handles all our memory management.FbxManager* lSdkManager = FbxManager::Create();// Create the IO settings object.FbxIOSettings *ios = FbxIOSettings::Create(lSdkManager, IOSROOT);lSdkManager->SetIOSettings(ios);// Create an importer using the SDK manager.FbxImporter* lImporter = FbxImporter::Create(lSdkManager, "");// Use the first argument as the filename for the importer.if (!lImporter->Initialize(lFilename, -1, lSdkManager->GetIOSettings())) {printf("Call to FbxImporter::Initialize() failed.\n");printf("Error returned: %s\n\n", lImporter->GetStatus().GetErrorString());exit(-1);}// Create a new scene so that it can be populated by the imported file.FbxScene* lScene = FbxScene::Create(lSdkManager, "myScene");// Import the contents of the file into the scene.lImporter->Import(lScene);// The file is imported; so get rid of the importer.lImporter->Destroy();//获取场景中根节点，然后对其调用自定义的StoreNormalsToVertColor函数	FbxNode* lRootNode = lScene->GetRootNode();if (lRootNode) {StoreNormalsToVertColor(lRootNode);}//导出Fbx文件FbxExporter* lExporter = FbxExporter::Create(lSdkManager, "");bool lExportStatus = lExporter->Initialize(lFilename2, -1, lSdkManager->GetIOSettings());if (!lExportStatus) {printf("Call to FbxExporter::Initialize() failed.\n");printf("Error returned: %s\n\n", lExporter->GetStatus().GetErrorString());return false;}lExporter->Export(lScene);lExporter->Destroy();// Destroy the SDK manager and all the other objects it was handling.lSdkManager->Destroy();return 0;
}

经过以上两种方案处理后的模型，在Unity shader中通过读取顶点颜色中的法线信息，然后将其转换到模型空间下与模型顶点坐标相加即可挤出轮廓线模型，shader中轮廓线pass代码如下：

		Pass{NAME "OUTLINE"Cull FrontCGPROGRAM#pragma vertex vert#pragma fragment frag// make fog work#pragma multi_compile_fog#include "UnityCG.cginc"struct a2v{float4 vertex : POSITION;float3 normal : NORMAL;float4 tangent : TANGENT;float4 vertexColor : COLOR0;};struct v2f{UNITY_FOG_COORDS(1)float4 vertex : SV_POSITION;};fixed4 _OutlineColor;half _OutlineWidth;v2f vert(a2v v){v2f o;//从顶点颜色中读取法线信息，并将其值范围从0~1还原为-1~1float3 vertNormal = v.vertexColor.rgb * 2 - 1;//使用法线与切线叉乘计算副切线用于构建切线→模型空间转换矩阵float3 bitangent = cross(v.normal,v.tangent.xyz) * v.tangent.w * unity_WorldTransformParams.w;//构建切线→模型空间转换矩阵float3x3 TtoO = float3x3(v.tangent.x, bitangent.x, v.normal.x,v.tangent.y, bitangent.y, v.normal.y,v.tangent.z, bitangent.z, v.normal.z);//将法线转换到模型空间下vertNormal = mul(TtoO, vertNormal);//模型坐标 + 法线 * 自定义粗细值 * 顶点颜色A通道 = 轮廓线模型					o.vertex = UnityObjectToClipPos(v.vertex + vertNormal *_OutlineWidth * v.vertexColor.a);UNITY_TRANSFER_FOG(o,o.vertex);return o;}fixed4 frag(v2f i) : SV_Target{// apply fogUNITY_APPLY_FOG(i.fogCoord, _OutlineColor);return _OutlineColor;}ENDCG}

Unity中轮廓线显示效果如下（模型颜色为顶点色）：

一个部分光滑部分硬边的球体轮廓线效果如下：


简单做了一个骨骼动画，轮廓线也没有出现问题：

以上都是非常简单的测试，以后发现问题再解决，就这样