Contour-Hugging Heatmaps for Landmark Detection阅读笔记

本文主要是介绍Contour-Hugging Heatmaps for Landmark Detection阅读笔记，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

代码：https://github.com/jfm15/ContourHuggingHeatmaps

我自己稍微改了一点的https://github.com/Nightmare4214/ContourHuggingHeatmaps

摘要

希望输出landmark的位置和每个landmark的不确定度(Uncertainty)

作者主要贡献：

作者通过分类的方式来训练模型
通过temperature scaling来校准模型的不确定度
利用Expected Radial Error(ERE)来获取不确定度

背景

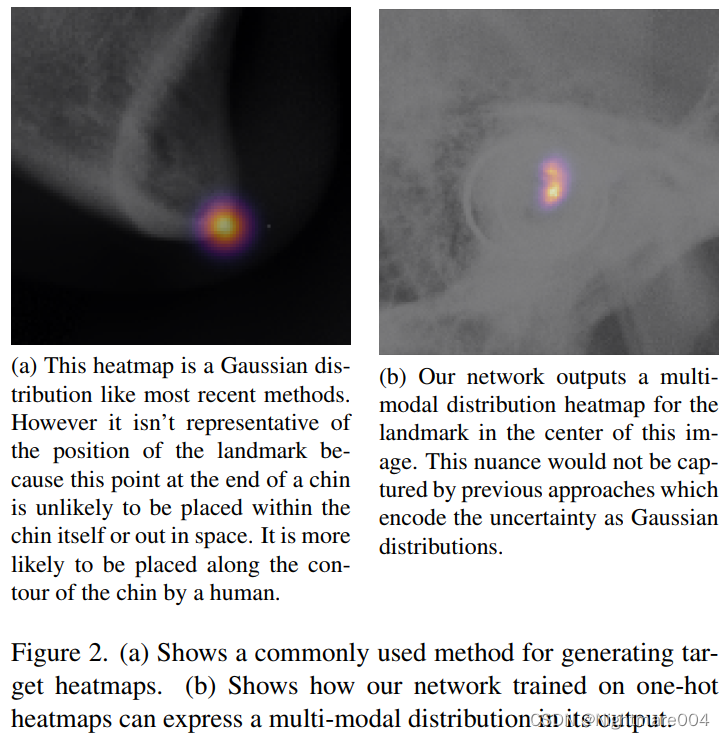
一般的模型回归的是服从高斯分布的heatmap
但是不是所有地方都可能出现landmark，比如说一个landmark，他可能出现在骨头上，不会出现在旁边的软组织上，此时概率不应该是一个圆形的分布，而应该是集中在骨头上的

为了能够预测这种不规则形状，作者采用的是分类的方法，而不是回归高斯heatmap
在这里插入图片描述

方法

模型

编码器用的在imagenet预训练的resnet34，解码器是Unet的解码器，最后接了一个 $1\times 1$ 的卷积调整通道输出每个landmark的概率图
其中第一层卷积通过sum，将原本3通道的，改成了1通道

监督信号是one-hot的heatmap（每个landmark有1个对应的heatmap，每个heatmap只有landmark那个位置是1，其他都是0）
模型经过2d softmax，然后用交叉熵计算损失，相当于是做分类/分割问题

temperature sacling

$\sigma_l(i, j)=\frac{e^{\frac{c_l(i, j)}{T_l}}}{\sum_{s=1}^w \sum_{t=1}^h e^{\frac{c_l(s, t)}{T_l}}}$
简单来说就是除以一个T之后用softmax

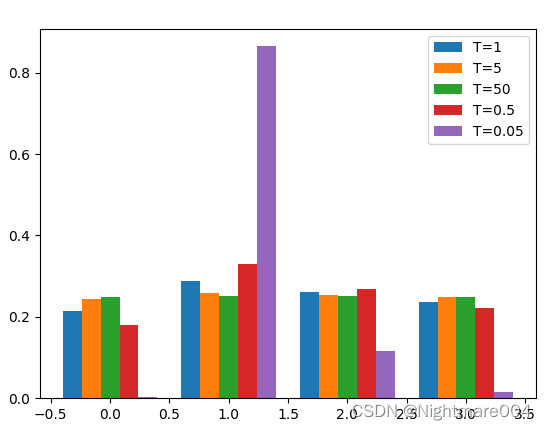
temperature scaling不改变模型的精度（因为softmax是单调函数），但是可以改变方差

如下图，可以看到T越小差距越大，T越大差距越小
在这里插入图片描述

#!/usr/bin/env python
# _*_ coding:utf-8 _*_
import matplotlib.pyplot as plt
import numpy as npdef softmax(x, T):x = np.exp(x / T)return x / x.sum()if __name__ == '__main__':x = np.arange(4)origin = np.array([0.1, 0.4, 0.3, 0.2])temperatures = [1, 5, 50, 0.5, 0.05]total_width, n = 0.8, len(temperatures)width = total_width / nx = x - (total_width - width) / 2for i, temperature in enumerate(temperatures):plt.bar(x + i * width, softmax(origin, temperature), width=width, label=f'T={temperature}')plt.legend()plt.show()

不确定度

Expected Radial Error (ERE)
$E_{\sigma_l}=\sum_{i=1}^w \sum_{j=1}^h \sigma_l(i, j) \sqrt{(i-\tilde{x})^2+(j-\tilde{y})^2}$
其中 $\left(\tilde{x}, \tilde{y}\right)$ 是预测landmark坐标
$\sigma_l(i, j)$ 是heatmap，但是需要预处理一下
去除了小于最大值 $5\%$ 得点，然后通过除以总和进行归一化

下面作者通过实验，表明ERE和径向误差（预测landmark到真实landmark的距离）是有关系的

验证

Reliability Diagrams

下面说的landmark的置信度指的是对应的heatmap的最大值

设置信度的最大值为 $M$ (这里最大值指的是所有图片所有landmark的置信度)
根据 $M$ 分成10个桶(bin)，每个桶长度为 $\frac{M}{10}$
将所有图片所有landmark划分到对应的桶

每个桶的平均置信度就是landmark的平均置信度

一个landmark如果和真实的landmark完全重合，则称为预测正确
每个桶的正确率就是预测正确的比例
（其实想完全重合基本不可能，所以代码里是 $<=\sqrt{\frac{pixel\_size^2}{\pi}}=\sqrt{\frac{(\frac{1935}{640}\times 0.1)^2}{\pi}}$ ）

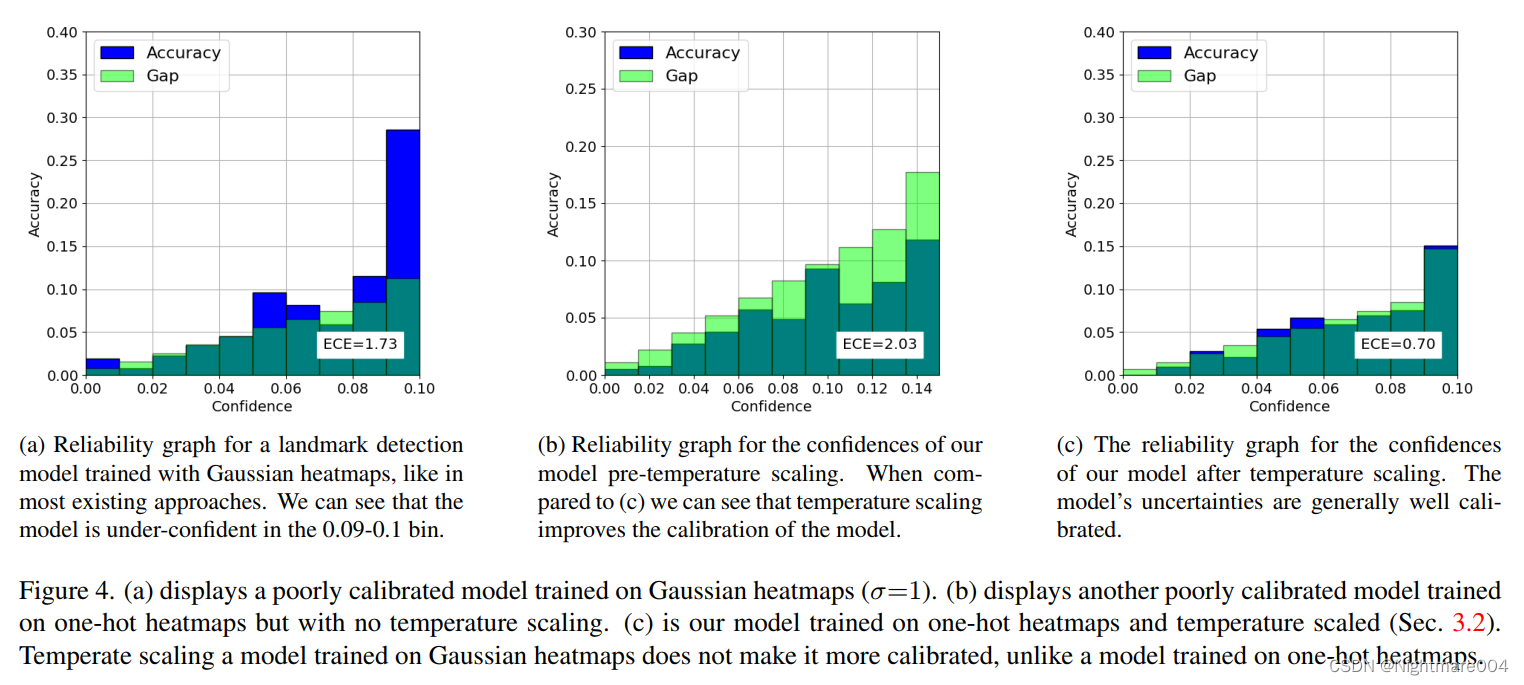
Expected Calibration Error (ECE)就是每个桶正确率和平均置信度的差值的绝对值的期望
$\mathbb{E}\left[\left|acc-confidence\right|\right]$
如果一个模型预测的完美校准(perfectly calibrated)，那么正确率和平均置信度一样（这句话我也没理解）

通过temerature scaling，作者把ECE从2.03降到了0.70
在这里插入图片描述

ERE

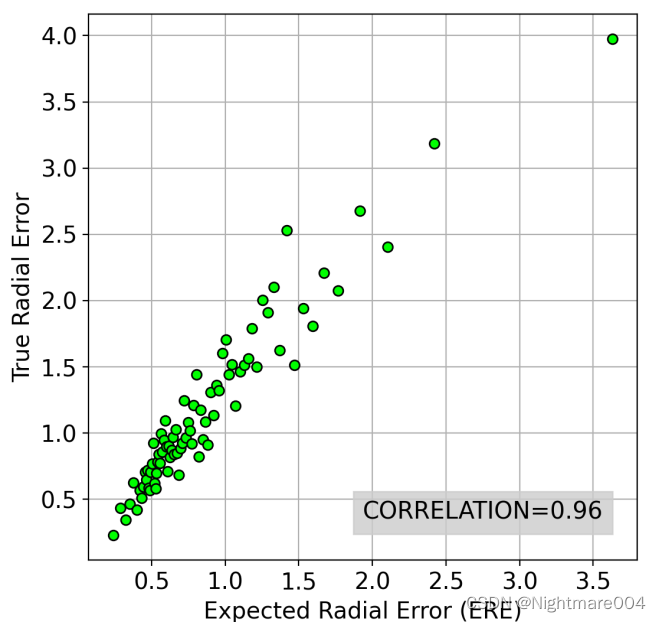
作者想表明ERE和径向误差是相关的

针对所有图的所有landmark，按照ERE排序，每36个代表图上的一个点，然后算皮尔逊

能看得出来这里几乎正相关
在这里插入图片描述

通过ERE来区分预测的准确性

通过ERE设定一个阈值来判断一个landmark是否不准确/错误（inaccurate / ‘erroneous’）
1.在测试集1使用模型得到heatmap
2.找到每张heatmap的最大值，作为预测的landmark，然后计算ERE
3.计算径向误差，<2mm就是good, >2mm就是erroneous
4.画ROC曲线，其中真阳性(true positive)就是ERE>阈值且真实径向误差>2mm，
假阳性(false positive)就是ERE>阈值且真实误差<2mm

最后选定真阳性率(true positive rate)为0.5的阈值作为设定的阈值
论文里是1.414，也就是说，如果ERE>1.414,就认为这是erroneous
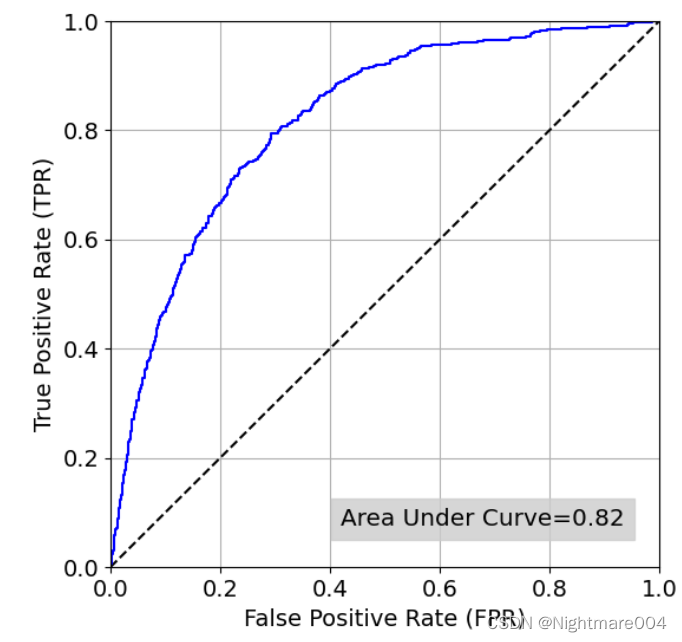
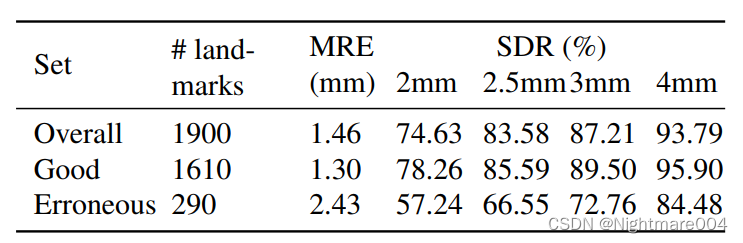
在这里插入图片描述
在测试集2上利用这个阈值来判断一个landmark的准确性
最后确实good的landmark更加准确