P1119 灾后重建（Floyd算法优化）

本题是一道Floyd算法的应用。

Floyd算法是基于动态规划方程的推导而来，利用每一个合理的中间点来实现对两点之间距离的更新，具体的状态表达方程为：

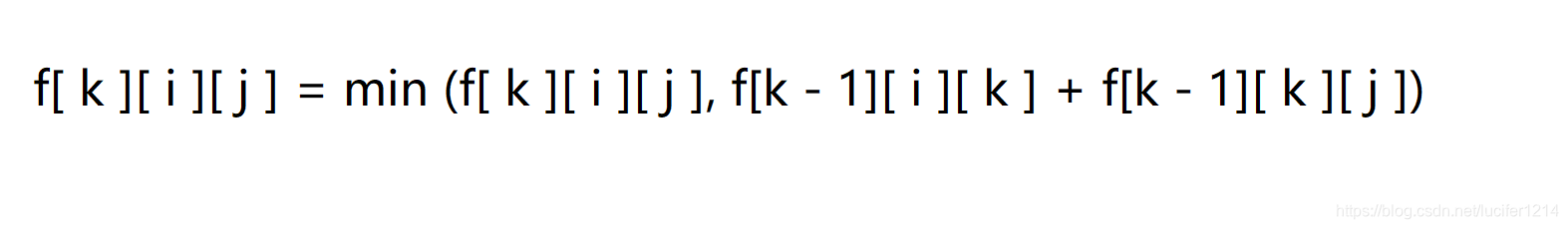
其中还有一些细节需要注意，本题给出了每一个村庄重建的时间，而这就需要我们额外注意，如果我们每次进行Floyd算法求询问中的两点最短路径那么时间复杂度就为O（q * n^3）,显然已经超过了我们的所给时间，而事实也是这样，只能得50分，tle了5个点。

那么我们就需要对Floyd算法进行一些简单的优化，由于题干中给到，每次询问的时间都是不降的（果然高中老师说的对呀，题干没有废话），那么我们就可以按照每次询问的时间，分别按顺序更新每个中间点，这样我们就将时间复杂度大大缩减，达成了我们的目的。

来看一下代码叭。

#include<iostream>
#include<stack>
#include<algorithm>
#include<cstring>
#include<string>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
const int p = 1e9 + 7;
typedef pair<int, int> pii;
const int N = 310;
int tim[N];
ll n, m;
int g[N][N];
void init() {//初始化邻接矩阵for (int i = 0; i <= n; i++)for (int j = 0; j <= m; j++){if (i == j) g[i][j] = 0;else g[i][j] = 0x3f3f3f3f;}}
int main()
{cin >> n >> m;init();for (int i = 0; i < n; i++)cin >> tim[i];for (int i = 1; i <= m; i++) {int a, b, c;cin >> a >> b >> c;g[a][b] = g[b][a] = c;//存无向图}ll q;cin >> q;int k = 0;while (q--){int x, y, z;cin >> x >> y >> z;if (tim[x] > z || tim[y] > z) {cout << -1 << endl;continue;}while (k < n && tim[k] <= z) {//按照所给的时间来更新中间点（原为for(int k = 0; k < n; k++)）for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {g[i][j] = min(g[i][j], g[i][k] + g[k][j]);}}k++;}if (g[x][y] < 0x3f3f3f3f) {cout << g[x][y] << endl;}else cout << -1 << endl;}
}