【HDL系列】进位旁边加法器原理与设计

本文主要是介绍【HDL系列】进位旁边加法器原理与设计，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、进位旁边加法器

进位旁路加法器（Carry Skip Adder，CSA），也称Carry Bypass Adder。需要注意的是，CSA也是另外一种加法器——进位保存加法器（Carry Save Adder）的简称，关于这种加法器后期会介绍。

此前介绍了行波进位加法器RCA，第k位的进位Ck必须等待之前的Ck-1的结果才能计算出来，如下图进位c16必须等到前一级全加器的c15输出才可以计算，所以行波进位加法器的特点便是超长的进位传播链。

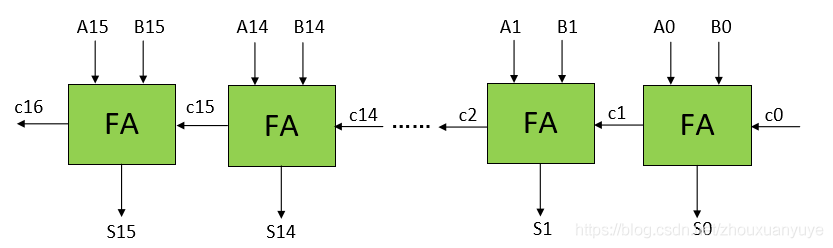
进位旁边加法器的思想在于加速进位链的传播，在某种情况下，到达第i位的进位无需等待第i-1位进位。在16比特RCA中，最长的进位链为c0->c1->c2->…->c16，也就是说，每一位全加器都有进位，这条路径也是最长的关键路径。进位旁边加法器通过加入旁路逻辑来缩短这条最长路径，该旁路逻辑由2选1数据选择器，第x级进位和第y级进位和进位bypass信号组成。

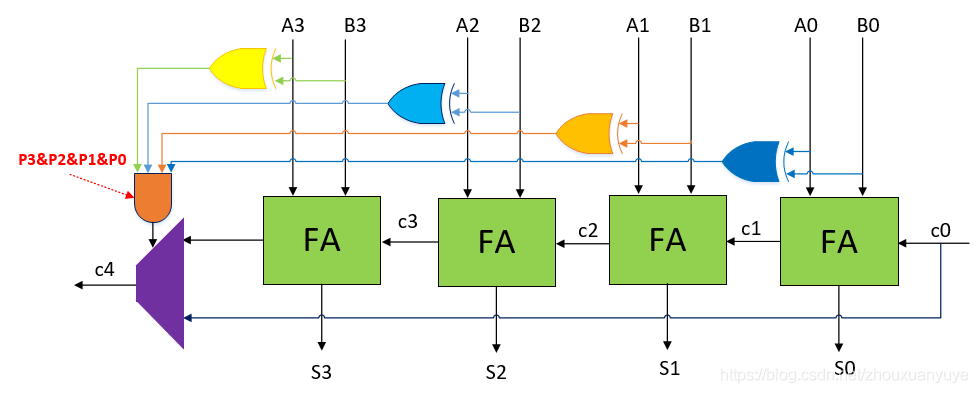
CSA结构如上，紫色部分为数据选择器，橙色部分为数据选择信号，数据来源为进位c0和第3个全加器的进位输出。

当P3&P2&P1&P0=1时c4=c0；进位c0直接传播至c4，而不需再经过4级全加器的延迟，这就是进位旁路加法器的核心。

为什么P3&P2&P1&P0=1时c0可以直接传播至c4？乍一看这个问题有点让人困扰。

先看c4的生成逻辑：

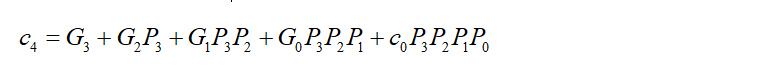
当P3&P2&P1&P0=1时，则P3=P2=P1=P0=1，所以c4生成逻辑如下：

在介绍超前进位加法器中，我们定义了PG：

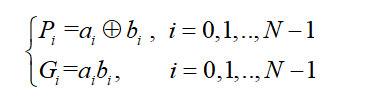
P是a与b异或的结果，只有a=0，b=1或者a=1，b=0时，P才可能等于1，而G=ab，所以只要P=1，G则一定为0，所以G3=G2=G1=G0=0。

最后结论与上述一致：当P3&P2&P1&P0=1时，c4的生成逻辑最终变成c4=c0。

二、进位旁路加法器关键路径与优化

将N比特加法器，以m比特为一组，分成N/m组，如下式16比特进位旁路加法器，N=16，m=4，共有4组，该16比特CSA由4比特CSA级联而成，其中4比特CSA由4个全加器组成的Block，进位逻辑Skip logic和2选1数据选择器三部分组成。

以上关键路径发生在：

c0走第一级Block，经过4级全加器，进位从bit0到bit3生成c4。
中间进位经过bypass逻辑。
最后一级走Block逻辑，经过4级全加器，进位从bit12到bit15生成c16.

基于此结构通用的关键路径延迟公式为：

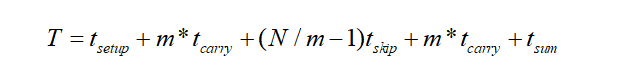
其中：

Tsetup：A,B低位到第一级block的时间

tcarry：每个进位传播Block中全加器产生进位的时间

Tskip：进位通过skip逻辑的时间

Tsum：从最后个进位到S输出的时间

可能在此处读者会有一个疑问，为什么最长的delay会是中间两级路径，如果加法器进位全部走Block逻辑，应该具有更长的延迟啊？其实走最长的路径，中间路径会被旁路，也就是执行0111_1111_1111_1111 + 0000_0000_0000_0001的情况。第一级进位产生后，中间两级被旁路，最后一级经过RCA进位链，也就是下图中红色描绘出的路径图。

三、进位旁路加法器Verilog设计

以下参数化cska（Carry Skip Adder, 为防止混淆取名cska）基于4比特cska设计，width可参数化定义为4的倍数，如20,24,32，64,128等。

默认16比特进位旁路加法器，由4个进位旁路加法器级联而成，每个进位旁路加法器中由4个全加器级联，且有进位旁路逻辑。

module cska #(width=16) (input  [width-1:0] op1,input  [width-1:0] op2,output [width-1:0] sum,output cout
);wire [width>>2:0] c;
assign c[0] = 0;
assign cout = c[width>>2];genvar i;
generate for( i=0; i<width>>2; i=i+1) begincska_4bit u_cska_4bit (.op1( op1[i*4+3:i*4] ),.op2( op2[i*4+3:i*4] ),.cin( c[i] ),.sum( sum[i*4+3:i*4] ),.cout( c[i+1]));end
endgenerateendmodule

cska_4bit模块中进位链和进位旁路逻辑：

//full adder and p generator
genvar i;
for( i=0; i<width; i=i+1) beginfull_adder_cska u_full_adder_cska(.a   ( op1[i]   ),.b   ( op2[i]   ),.cin ( c[i]     ),.cout( c[i+1]   ),.s   ( sum[i]   ),.p   ( p[i]     ));
end//carry bypass
assign sel = p[0] & p[1] & p[2] & p[3];
assign cout = sel ? cin : c[width];

Verilog源码公众号回复004。

欢迎指正错误，更多阅读，关注“纸上谈芯”，不定期更新，共同学习: