本文主要是介绍图及谱聚类商圈聚类中的应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
背景
在O2O业务场景中,有商圈的概念,商圈是业务运营的单元,有对应的商户BD负责人以及配送运力负责任。这些商圈通常是一定地理围栏构成的区域,区域内包括商户和用户,商圈和商圈之间就通常以道路、河流等围栏进行分隔。
对某些业务应用,商圈可能太小,需要将几个到十几个商圈划成一片,按商圈片进行运营。这类划分通常无法纯粹按照商圈地理位置来划分,因为商圈是一个连着一个的。因此,还需要找到商圈之间的其他关联指标,从业务上来说,如果两个商圈的用户重合度很高(比如A商圈中的80%的用户也是B商圈的用户,反之亦然)或者两个商圈的配送运力重合度和高(比如A商圈中的80%的骑手也是B商圈的骑手),那么这两个商圈可以划成一类,因此,用户、配送运力重合度都可以作为商圈之间的关联指标。
本文介绍了一种使用谱聚类对商圈进行聚类的方法。
商圈之间关系图构造
把商圈和商圈之间的联系构造为图,具体为:每个商圈是图中的节点,商圈和商圈之间共享用户数占比或者运力占比作为图的边,就可以得到一个城市所有商圈两两之间关系图。
比如,商圈之间的关系数据如下:
| 商圈-source | 商圈-target | 商圈关联指标-weight |
| 73***8 | 9***7 | 71.3% |
| 73***8 | 9***1 | 70.1% |
| 73***8 | 1***51 | 66.2% |
| 73***8 | ... | ... |
| 73***8 | 1***27 | 0.6% |
| 73***8 | 1***95 | 0.6% |
| 73***8 | 7***0 | 0.6% |
使用networkx可以将上述数据转化为关系图。networkx是Python的一个包,用于构建和操作复杂的图结构,提供分析图的算法。图是由顶点、边和可选的属性构成的数据结构,顶点表示数据,边是由两个顶点唯一确定的,表示两个顶点之间的关系。
对于networkx创建的无向图,允许一条边的两个顶点是相同的,即允许出现自循环,但是不允许两个顶点之间存在多条边,即出现平行边。边和顶点都可以有自定义的属性,属性称作边和顶点的数据,每一个属性都是一个Key:Value对。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import networkx as nx# 从数据构造图
g = nx.Graph()
g.add_weighted_edges_from(df_cluster.values)# 图可视化方法一
nx.draw(g, with_labels = True) ### 画可视化方法二
durations = [i['weight'] for i in dict(g.edges).values()]
labels = {i:i for i in dict(g.nodes).keys()}fig, ax = plt.subplots(figsize=(10,6))
pos = nx.spring_layout(g)
nx.draw_networkx_nodes(g, pos, ax = ax, label = True)
nx.draw_networkx_edges(g, pos, width = durations, ax = ax)
_ = nx.draw_networkx_labels(g, pos, labels, ax = ax)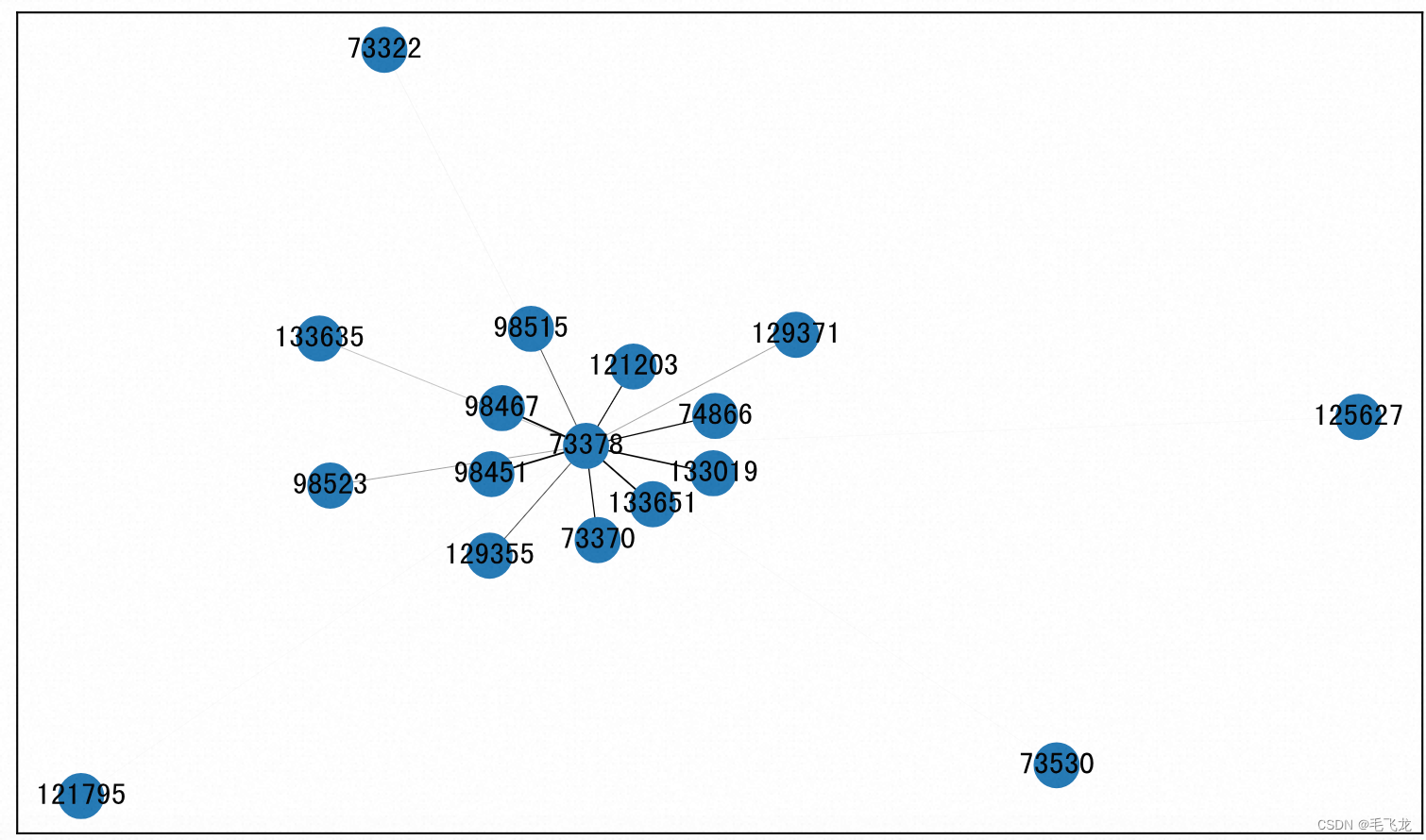
商圈聚类
基本思想
这里使用谱聚类的方法。谱聚类是从图论中演化出来的算法,后来在聚类中得到了广泛的应用。它的主要思想是把所有的数据看做空间中的点,这些点之间可以用边连接起来。如果把这些连线加上一个权重,就叫做加权图。
如果连线越长则权重越小,连线越短则权重越大,然后把权重最小的边切断,使得一个图变成两个图,便完成了一次聚类,这就是谱算法的基本思路,而其基本流程,就是构图->切图。
所以,问题来了,如何构图?若将所有的点都连接起来,这显然有些离谱,毕竟这种平方级别的复杂度不是一般内存能吃得消的,作为有一点聚类基础的人,第一时间就会想到KNN算法,即k近邻。
由于谱聚类中,两个点是否要被切断,最关键的因素是短边而非长边,所以只要将点与其最近的k个点连接起来就行了。这样得到的图有一个问题,即x最近的k个点中可能有y,但y最近的k个点中可能没有x,像极了女神和你。
对此有两种解决方案,一种是x也不要y了,另一种是强制让x加入到y的近邻中。
除了k近邻之外,还可以定死一个距离r,凡是距离小于r的都连线,大于r的都不连线。由于点和点之间的距离往往相差较大,故其权重一般会在距离的基础上做一些变换,这个变换在下文乘坐权重函数。
数据转换
这里使用sklearn.cluster.SpectralClustering进行聚类,需要将图g的数据转换为sklearn.cluster.SpectralClustering输入的形式,可以通过临接矩阵来实现。
from sklearn.cluster import SpectralClustering# 得到图的邻接矩阵
adj_matrix = nx.adjacency_matrix(g) # 将节点之间的边信息转换为矩阵的形式,比如matrix[0]表示第1个样本和其他样本之间的关联信息# 可以用nx.adjacency_matrix(g).todense()看邻接矩阵的具体内容nx.adjacency_matrix(g).todense()[0]matrix([[0. , 0.10247934, 0.10582011, 0.27272727, 0.41962422,0.01342282, 0.0210728 , 0.0075188 , 0.48453608, 0.4038055 ,0.04 , 0.43896104, 0.0528109 , 0.00930233, 0.02754821,0.00704225, 0.14554795, 0.03125 , 0.03814714, 0.03878116,0.36616162, 0.0083682 , 0.008 , 0.00487805, 0.12539185,0. , 0. , 0. , 0. , 0. ,0. , 0. , 0. , 0. , 0. ,0. , 0. , 0. , 0. , 0. ,0. , 0. , 0. , 0. , 0. ,0. , 0. , 0. , 0. , 0. ,0. , 0. , 0. , 0. , 0. ,0. , 0. ]])聚类
# 调用谱聚类模型
sc_model = SpectralClustering(n_clusters=3, # 非常重要的超参数affinity='precomputed',assign_labels='discretize', random_state=0)
clustering = sc_model.fit(adj_matrix)# 聚类结果
print(clustering.labels_)[2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 0 1 1 2 1 2 1 1 1 1 2 1 2 2 2 2 2 2 22 2 2 2 2 2 2 2 2 2 2 2 2 2 0 0 2 2 2 2 2 2 2 2 2 0 0 2 0 2 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 0 2 2 22 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 0]注意,上述聚类结果中对于模型的超参数n_clusters,我们直接设置成了3,这是非常随意的。如果事前没有聚类数的目标期望,一般我们可以尝试不同的的聚类数,然后基于一定的评估标准(此处选择轮廓分),选择最好的聚类数进行聚类。
from sklearn import metrics# 设置不同的聚类数超参数,通过轮廓分评估标准选择最佳聚类数n_clusters_list=[2,3,4,5,6,8,10,12,14,16,18,20]
score_list=[]
for k in n_clusters_list:sc_model = SpectralClustering(n_clusters=k, affinity='precomputed',assign_labels='discretize', random_state=0)clustering = sc_model.fit(adj_matrix)pred_y=sc_model.fit_predict(adj_matrix)score=metrics.silhouette_score(adj_matrix,pred_y)score_list.append(score)plt.xlabel("n_clusters")
plt.ylabel("silhouette_score")
plt.scatter(x = n_clusters_list, y = score_list)
plt.show()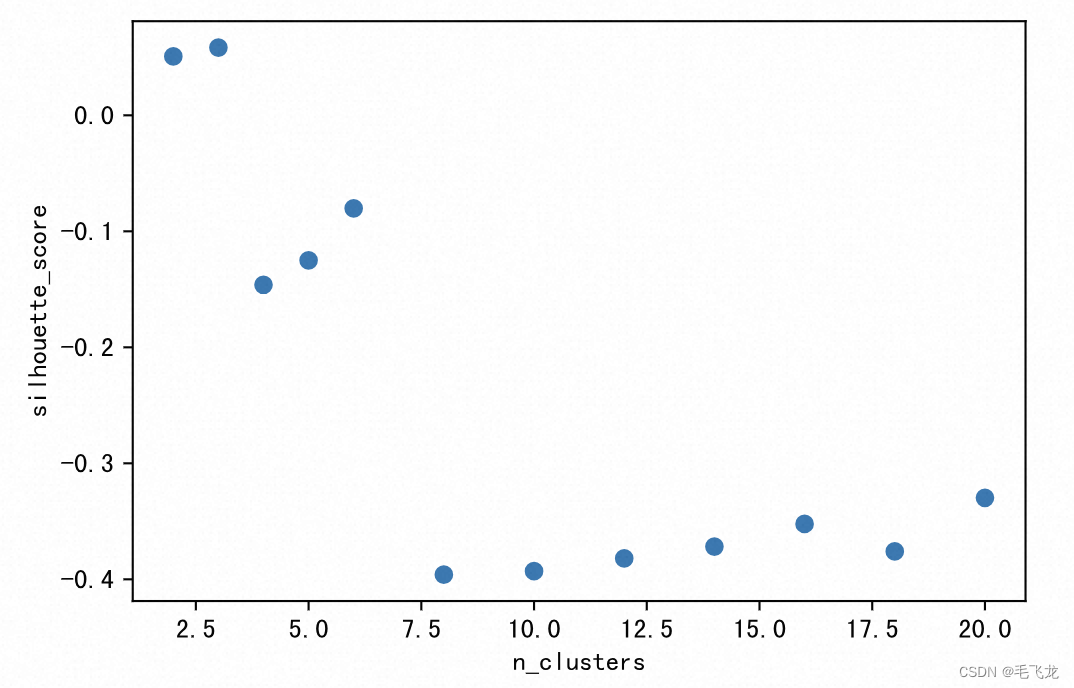
可见,本例中n_clusters = 3的轮廓分最高,因此我们可以设置聚类数为3。
结果展示
如果有商圈围栏的经纬度坐标数据,则可以使用keplergl来查看聚类后的效果。
# 聚类结果可视化check
import keplergl
amap = keplergl.KeplerGl(height = 800)
amap.add_data(data = df['scope_geojson','center_lng','center_lat','cluster_label'])
amap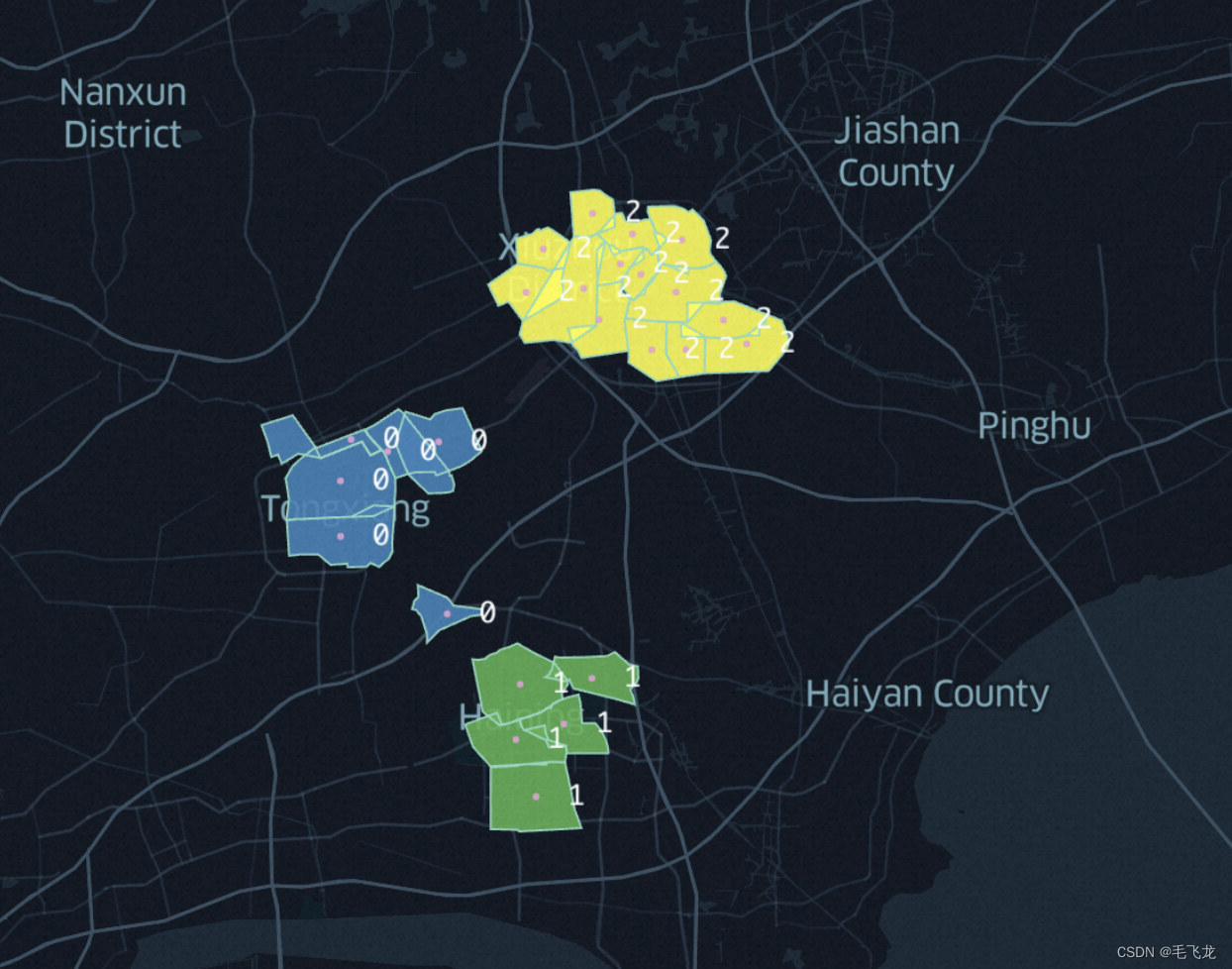
这篇关于图及谱聚类商圈聚类中的应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




