underactuated robotics lecture 1 笔记 --- Introduction

1. Introduction

最近因为目前的项目中，可能会用到一些基于动力学的planning 和control的算法，看了一下MIT欠驱动机器人的课程，通过记笔记的方式帮助自己查缺补漏。笔记基本上按照讲课的顺序进行梳理，穿插一些在matlab上实现的结果和个人的理解。

2 Motivation

2.1.1 Honda ASIMO vs passive dynamic walkers

ASIMO机器人的几大问题：
1）动作表现的想不了解自己的动力学；
2）使用高增益去follow desire trajectory(位置环控制)，导致能量损失很大；
3）只在一个很小的状态空间中是稳定的，导致了速度、效率远低于人类；

美国在上世纪八十年代搞出来的Passive dynamic walker(PDW), 表现的更像了人类。

2.1.2 Birds vs modern aircraft

人类的航天技术已经发展的很成熟了，但是距离鸟类代差是非常明显的。人类走的路线是非常强劲的发动机动力+动力学设计，和鸟类的代差是：
1）鸟类的能量效率非常高，飞几千公里也不怎么需要能量；
2）鸟类的操控性特别强，转向速度快；
3）对鸟类的数据研究相对困难，人类通过研究类似的海洋生物，它们的动力学性能令人惊叹。

2.1.3 manipulation

工业机械臂的发展和航天技术的发展类似，机械臂还无法帮助人类完成基础的家务。对于抓取任务，当前主流采用的pipeline为：1）设置机械臂上的抓取点；2）移动到预抓取点；3）进行盲抓。因为没有通过和物体接触去辨识物体动力学，导致很多动力学接触的抓取任务，容易失败。

2.1.4 总结

传统控制理论通过反馈去克服机器自身的动力学，控制工程师不愿意把情况搞定复杂。对于无驱动或者是驱动力受限的情况，工程师不得不考虑系统的动力学，合理的利用动力学则能改善系统的效率、灵活度和鲁棒性。最优控制提供一条可行的方案，现实中的非线性系统则是一个拦路虎。

2.2 动力学系统定义

对于大部分的动力学系统(机械、液压、电气系统)的一般定义为一个二阶系统：
$$\ddot{q}=f(q,\dot{q},u,t)$$
大部分系统可以写成affine 形式：
$$\ddot{q}=f_1(q,\dot{q},t)+f_2(q,\dot{q},t)u$$

两种情况下，系统可以看成是欠驱动的。欠驱动系统可以看成我想控制机器人系统中的某些状态量，但是无法直接控制，需要通过系统整体的力学，通过 状态方程关联(力学传导) 的方式进行控制。
1）$dim(f_2(q,\dot{q},t))<dim(q)$,驱动关节小于状态的自由度；
机械臂处于singularity时，不能算欠驱动的；
机械臂的虽然有限位，但是它也不需要使用限位的工作空间，这种也不算欠驱动系统；
2）输入u是受限的；

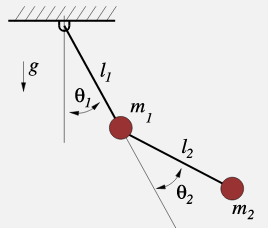
• double pendulum system
  对于典型的倒立摆系统，动力学方程可以写成：
  $$M(q)\ddot{q}+c(q,\dot{q})\dot{q}={\tau }_g(q)+Bu$$

完整的动力学方程如下：

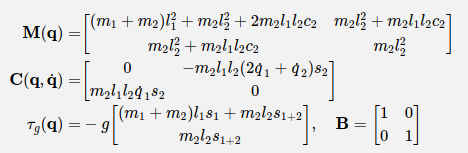
判别是否是欠驱动系统：
$$\ddot{q}=M^{-1}(q)[{\tau }_g(q)+Bu-C(q,\dot{q})\dot{q}]$$

$M^{-1}(q)$是满秩的，只有B是满秩的，机械臂系统才是一个全驱动系统。

问题1： 欠驱动和机械臂奇异点(singularity)的关系。
奇异点关注是末端的受力。
$$F=J\ast \tau$$
机械臂处于奇异点是，jacobian矩阵的秩降低，导致末端的受力在某个方向上不可控。
问题2：检验动力学公式。
使用simscape multi-body检验动力学公式是否正确，如果公式错误就不断减少影响因素(重力加速度、阻尼项、角度)
关节的摩擦阻力可以看成是外界的扰动力，在控制力基础上-b*w

2.3 feedback equivalence

对于最简单的连杆机器人，都存在着非线性，如上面double pendulum的动力学方程。先来看全驱动机器人能怎么处理这种非线性。
$$\begin{array}{rl}u& =\pi (q,\dot{q},t)=f_2^{-1}(q,\dot{q},t)[u^{\prime }-f_1(q,\dot{q},t)]\\ \ddot{q}& =u^{\prime }\end{array}$$

u’可以看成是间接的输入，想要系统实现什么样的加速度，就给什么样的u’，再根据已有的模型，推算实际的输入u。
1）精确的模型，消除了非线性的因素，通过换算消除了非线性；
2）$dim(f_2)=dim(q)$,但是$f_2$不是square，$f_2$的解不是唯一，是一个解集空间，再继续发展可以搞出分级控制。

• feedback cancellation on the double pendulum
  希望double pendulum 表现的像单个倒立摆，也就是说$\ddot{q_2}=0$
  1)步骤1:计算u’: 现在是个线性控制器，直接把PID搬上来,不用反馈控制器当然是无法做到稳定的表现的像一个单杆。
  $$u^{\prime }=-k_p\ast \theta -k_d\ast \dot{\theta }$$
  2)步骤2:计算实际的u;
  $$u=B^{-1}\ast (M\ast u^{\prime }-\tau +C\ast \dot{q})$$

全驱动系统可以看成是$\ddot{q}=u^{\prime }$,但是欠驱动系统就要复杂的多。

2.4 Input and state constraints

工程实际中，往往某个关节缺少驱动源的情况较少，更多的情况是：驱动源的驱动能力受限；状态空间中很多地方是不安全的也受限。这两种情况都会导致控制器的输入维度降低，进而造成一种欠驱动的情况。

2.4.1 Nonholonomic constraints

• 非完整约束一般描述环境对机器的限制，如差速轮系统，无法直接产生侧向移动，但是它的位置空间的维度并没有降低(仍然是想去哪就去哪)。 非完整约束的代数形式为：
  $$\varphi (q,\dot{q},t)=0$$
• 完整约束 holonomic constraints
  环境对机器的约束加强了，位置空间上的很多位置是去不了的,例如火车的轨道。
  $$\varphi (q,t)=0$$

2.5 Underactuated robotics

很多机器人都是欠驱动系统
1）足式机器人，足式机器人的状态一般描述为关节+主体的6个自由度，所以是欠驱动的；
2）仿真鱼和昆虫机器人，情况和足式机器人一样，都需要通过关节间接的控制身体。
3）机械臂，一般来讲末端的物体有6个自由度，如果关节数目小于6，也符合欠驱动机器人的定义了。