【数据结构】数组和字符串（十五）：字符串匹配2：KMP算法（Knuth-Morris-Pratt）

本文主要是介绍【数据结构】数组和字符串（十五）：字符串匹配2：KMP算法（Knuth-Morris-Pratt），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

4.3 字符串

  字符串(String)是由零个或多个字符(char)顺序排列组成的有限序列，简称为串。例如 “good morning”就是由12个字符构成的一个字符串。一般把字符串记作：

$$S{=}^{\prime \prime }{a}_0{a}_1\dots a_{n-1}^{\prime \prime }$$

  其中S是串名，引号中的字符序列是串值。字符个数是串的长度，长度为0的串被称为空串，因为它不包含任何字符。需要注意的是，空格字符（" "）并不是空串，因为它包含一个字符——空格。
  若把某个串称为主串，则主串中任意个连续的字符组成的子序列被称为子串。子串在主串中第一次出现时，其首字符在主串中的序号被称为该子串在主串中的位置。
  关于字符串的基础知识亦可参考前文：
【重拾C语言】六、批量数据组织（三）数组初值；字符串、字符数组、字符串数组；类型定义 typedef
【重拾C语言】七、指针（三）指针与字符串（字符串与字符串数组；指针与字符串的遍历、拷贝、比较；反转字符串）

4.3.1 字符串的定义与存储

  字符串在许多非数值计算问题中扮演着重要的角色，并在模式匹配、程序编译和数据处理等领域得到广泛应用。在高级程序设计语言中，字符串通常被定义为以特殊字符’\0’（称为空字符或字符串结束符）结尾的字符序列。这个约定使得在处理字符串时可以方便地确定字符串的结束位置。关于字符串的存储方式，主要有两种常见的方式：

• 顺序存储：字符串的字符按照顺序依次存储在连续的内存空间中。这种方式使得字符串的访问和操作效率较高，可以通过索引直接访问任意位置的字符。在顺序存储方式中，字符串的长度可以通过计算字符个数或者遇到’\0’结束符来确定。

• 链式存储：字符串的字符通过链表的方式进行存储。每个节点包含一个字符和指向下一个节点的指针。链式存储方式可以动态地分配内存，适用于长度可变的字符串。但是相比于顺序存储，链式存储方式需要更多的内存空间，并且访问字符需要遍历链表。

  选择何种存储方式取决于具体的应用场景和需求。顺序存储适合于需要频繁访问和操作字符串的情况，而链式存储适合于长度可变的字符串或者对内存空间要求较高的情况。具体C语言实现可参照前文：
  【数据结构】数组和字符串（十一）：字符串的定义与存储（顺序存储、链式存储及其C语言实现）

4.3.2 字符串的基本操作

顺序存储：【数据结构】数组和字符串（十二）：顺序存储字符串的基本操作（串长统计、查找、复制、插入、删除、串拼接）
链式存储：【数据结构】数组和字符串（十三）：链式字符串的基本操作（串长统计、查找、复制、插入、删除、串拼接）

4.3.3 模式匹配算法

  文本编辑器中常用的“查找”、“替换”和“全部替换”等基本的编辑操作就是最普通的模式匹配问题，即：在文本文件中查找串。它的查找过程可简单描述如下：给定两个字符串变量 S 和 P，其中目标串 S 有n个字符，模式串P有m个字符，m≤n . 从S的给定位置（通常为S的第一个字符）开始，搜索模式串P，如果找到，返回模式串P在S中匹配成功的起始位置；如果没找到（即S中没有P），则返回–1 .
  字符串匹配可以采用多种算法，包括朴素模式匹配算法、KMP（Knuth-Morris-Pratt）算法、Boyer-Moore算法等。这些算法的性能和效率各不相同，具体选择取决于应用的需求和文本数据的规模。

0. 朴素模式匹配算法

• 朴素模式匹配算法：【数据结构】数组和字符串（十四）：字符串匹配1：朴素的模式匹配算法（StringMatching）
    朴素模式匹配算法的优点是过程简单，缺点是效率低。在最坏情况下，该算法要匹配n-m+1次，每次匹配要做m次比较。本文将介绍更高效的模式匹配算法——KMP算法

1. ADL语言

2. KMP算法分析

待完善

3. 手动求失败函数

定义

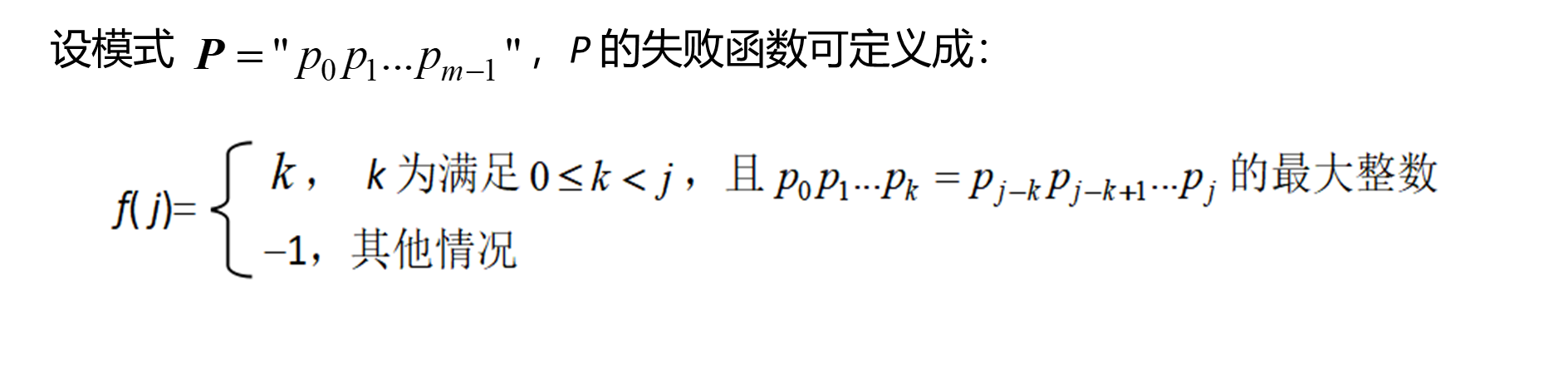
例1

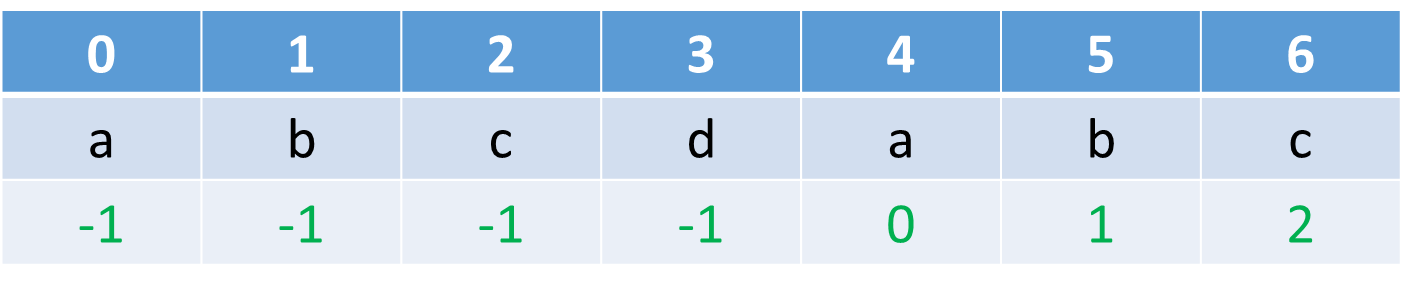
例2

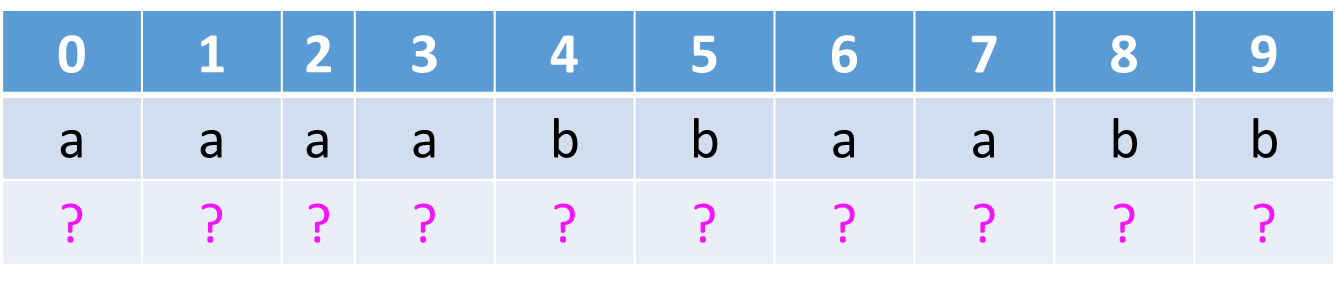
例3

答案见文末

4. 自动求失败函数（C语言）

#include <stdio.h>
#include <string.h>void buildFailureFunction(const char* P, int m, int* F) {int i = 1, j = 0;F[0] = -1;while (i < m) {if (P[i] == P[j]) {j++;F[i] = j - 1;i++;} else {if (j != 0) {j = F[j - 1];} else {F[i] = -1;i++;}}}
}int main() {
//    const char* P = "abcdabc";
//    const char* P = "aaaabbaabb";const char* P = "abcabcabcabcabcabc";int m = strlen(P);int F[m];buildFailureFunction(P, m, F);printf("模式串P: %s\n", P);printf("失败函数F(P): ");for (int i = 0; i < m; i++) {printf("%d ", F[i]);}printf("\n");return 0;
}

5. KMP算法（C语言）

#include <stdio.h>
#include <string.h>void buildFailureFunction(const char* P, int m, int* F) {int i = 1, j = 0;F[0] = 0;while (i < m) {if (P[i] == P[j]) {j++;F[i] = j;i++;} else {if (j != 0) {j = F[j - 1];} else {F[i] = 0;i++;}}}
}int kmpPatternMatching(const char* S, const char* P, int* comparisons) {int n = strlen(S);  // 目标串的长度int m = strlen(P);  // 模式串的长度int position = -1;  // 初始化位置为-1int F[m];  // 失败函数表buildFailureFunction(P, m, F);int i = 0, j = 0;while (i < n) {(*comparisons)++;  // 比较次数加1if (S[i] == P[j]) {i++;j++;if (j == m) {  // 如果模式串完全匹配position = i - m;break;}} else {if (j != 0) {j = F[j - 1];} else {i++;}}}return position;
}int naivePatternMatching(const char* S, const char* P, int* comparisons) {int n = strlen(S);  // 目标串的长度int m = strlen(P);  // 模式串的长度int position = -1;  // 初始化位置为-1for (int i = 0; i <= n - m; i++) {int j = 0;while (j < m && S[i + j] == P[j]) {(*comparisons)++;  // 比较次数加1j++;}if (j == m) {  // 如果模式串完全匹配position = i;  // 设置匹配位置break;}}return position;
}int main() {const char* S = "abcabcabcabcabcabd";const char* P = "abcabd";int comparisons = 0;  // 比较次数初始化为0int result1 = naivePatternMatching(S, P, &comparisons);if (result1 != -1) {printf("朴素模式匹配算法：模式串在目标串中的位置: %d\n", result1);} else {printf("未找到匹配\n");}printf("朴素模式匹配算法：比较次数: %d\n", comparisons);comparisons = 0;  // 比较次数初始化为0int result2 = kmpPatternMatching(S, P, &comparisons);if (result2 != -1) {printf("KMP算法：模式串在目标串中的位置: %d\n", result2);} else {printf("未找到匹配\n");}printf("KMP算法：比较次数: %d\n", comparisons);return 0;
}

6. 失败函数答案

例2

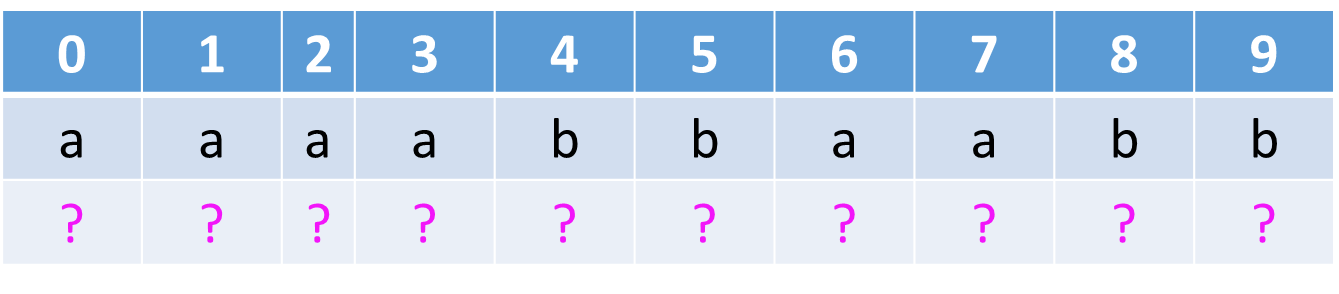
例3

这篇关于【数据结构】数组和字符串（十五）：字符串匹配2：KMP算法（Knuth-Morris-Pratt）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---