【Tsinghua】旅行商(TSP)

本文主要是介绍【Tsinghua】旅行商(TSP)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

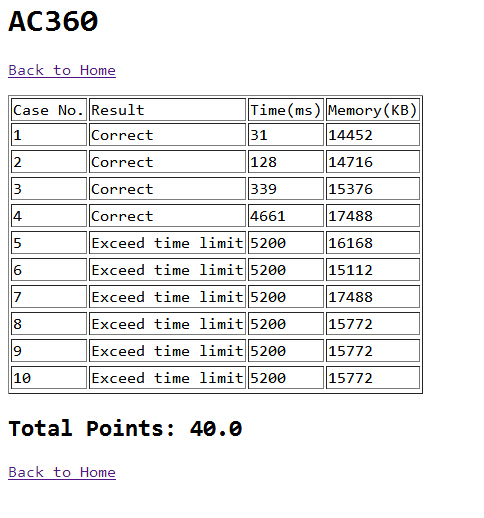
关于这道题，我要说两句，这道题我觉得我用拓扑排序的思路肯定是没错的，而且也对了几组数据，但是其他几组却超时，肯定是哪里的代码优化的不够好。。。。。。

最后只得了40分。。。

旅行商(TSP)

4 3
1 4
2 4
4 3

3

最后提交给那个OJ的代码：

#include<iostream>
#include <stdio.h>
#include <malloc.h>#define MAXSIZE 100002
#define TRUE 1
#define FALSE 0using namespace std;typedef int VertexData;
typedef int AdjType;//保存每个节点的最大路数
int Roads[MAXSIZE+1];
int maxRoad=0;typedef struct Stack          //定义栈
{int data[MAXSIZE+1];int top;
}Stack;typedef struct ArcNode		 //定义弧结点
{AdjType adj;ArcNode *nextArc;
}ArcNode;typedef struct VertexNode    //定义顶点
{VertexData vertexData;ArcNode *firstArc;
}VertexNode;typedef struct AdjMatrix     //定义图
{VertexNode vertexNodes[MAXSIZE+1];int verNum,arcNum;
}AdjMatrix;//全局变量
int indegree[MAXSIZE+1]={0};int LocateGraph(AdjMatrix *g, VertexData vertexData)
{int iIndex;for(iIndex=1;iIndex<=g->verNum;iIndex++){if(vertexData==g->vertexNodes[iIndex].vertexData)return iIndex;}return FALSE;
}void  CreateGraph(AdjMatrix *g)
{int iCount,arcStart,arcEnd;int start,end;//输入有向无环图的顶点,及弧数cin>>g->verNum>>g->arcNum;//输入有向无环图的顶点信息ArcNode *q=NULL;for(iCount=1;iCount<=g->verNum;iCount++){    g->vertexNodes[iCount].vertexData=iCount;g->vertexNodes[iCount].firstArc=NULL;}for(iCount=1;iCount<=g->arcNum;iCount++){//输入弧的起始与结束的信息cin>>start>>end;arcStart=LocateGraph(g,start);arcEnd=LocateGraph(g,end);//添加弧结点q=(ArcNode*)malloc(sizeof(ArcNode));q->adj=arcEnd;q->nextArc=g->vertexNodes[arcStart].firstArc;g->vertexNodes[arcStart].firstArc=q;//对于第arcEnd个顶点的入度值加1indegree[arcEnd]++;}
}//判栈空
int IsEmpty(Stack *stack)
{return stack->top==-1?TRUE:FALSE;
}//初始化栈
void InitStack(Stack *stack)
{stack->top=-1;
}//出栈
void Pop(Stack *stack,int *iIndex)
{*iIndex=stack->data[stack->top--];
}//进栈
void Push(Stack *stack,int value)
{stack->data[++stack->top]=value;
}//拓扑排序
void Tuopu(AdjMatrix *g)
{int iCount;Stack *stack=(Stack*)malloc(sizeof(Stack));InitStack(stack);ArcNode *p=NULL;//初始化 路数，都等于1for(iCount=1;iCount<=g->verNum;iCount++)Roads[iCount]=1;//对于入度为0的顶点入栈for(iCount=1;iCount<=g->verNum;iCount++){if(indegree[iCount]==0){Push(stack,iCount);}}//输出拓扑序列//输出顶点后，将与该顶点相连的顶点的边删除，将与相连顶点的入度减1，如减后为0，入栈，栈空结束while(!IsEmpty(stack)){Pop(stack,&iCount);//cout<<g->vertexNodes[iCount].vertexData<<" ";//这里处理路数p=g->vertexNodes[iCount].firstArc;while(p!=NULL){	if(--indegree[p->adj]==0)Push(stack,p->adj);if(Roads[g->vertexNodes[iCount].vertexData]+1>Roads[p->adj])Roads[p->adj]=Roads[g->vertexNodes[iCount].vertexData]+1;if(maxRoad<Roads[p->adj])maxRoad=Roads[p->adj];p=p->nextArc;}}//end while//cout<<endl;
}int main()
{AdjMatrix *g=(AdjMatrix*)malloc(sizeof(AdjMatrix));CreateGraph(g);Tuopu(g);printf("%d\n",maxRoad);return 0;
}

结果：

这篇关于【Tsinghua】旅行商(TSP)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！