本文主要是介绍压缩感知重构算法--MMP-BF和MMP-DF算法及其改进思路,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
MMP算法提出的文献:
Multipath Matching Pursuit----IEEE TRANSACTIONS ON INFORMATION THEORY
文章的作者也是gOMP算法的作者,现在在复旦大学任教
主要贡献:文章将传统贪婪算法的原子选择问题建模为组合树的搜索问题,为原子选择提供了新的思路。
在传统贪婪算法的改进中,不外乎以下几个方面:调整原子选择策略,调整原子相似性的准则等
其中调整原子选择策略又分为以下几种:
每次迭代选择单个原子(OMP),每次迭代选择多个原子(如:选择K个的CoSaMP算法,选择2K个的SP算法,选择S个的gOMP算法),通过阈值门限来进行原子选择,这样保证了每次迭代原子选择的灵活性,阈值则更贴近于观测矩阵和残差的内积变化规律(StOMP算法,SWOMP算法,TOMP算法等等)
在原子选择过程中,许多单向执行的算法可以结合CoSaMP算法中的回溯思想,来进一步提高重构精度。
在有步长设置的算法中,如何设置步长大小,是固定步长还是变步长,如果变的话,该如何改变,到目前为止均有学者做研究。而以上提到的算法都有一个共同的问题,就是只有一个候选集,单个候选集的原子选择模式会使得问题陷入局部最优解。而设置多个候选集则增大了搜索空间,提高了原子被正确选择的概率。这也是MMP算法的核心思想所在。
在论文中,作者提出了两种算法:MMP-DF和MMP-BF,分别是基于广度优先和深度优先的搜索策略。
所谓基于广度优先的多路径匹配追踪算法MMP-BF,顾名思义,我们在每次迭代的过程中,都有选出不同的原子放入多个候选集中,就如多叉数一样,基于根节点,每次迭代分出多少个子节点,可以人为设定。

上图展示了OMP算法和MMP算法的区别所在,在左图的OMP算法中,我们第一次选择出次序为2的原子,基于此,我们又选择出次序为1的原子,以此类推,当迭代次数为3的时候,我们会选出次序为2,1,4的三个原子放入支撑集中。
而对于MMP-BF算法来说,第一次选出了两个原子,分别为2和4,我们将其放入到两个不同的候选集中。第二次迭代的时候,我们以原子2为基础,选出了1和5,放入不同的候选集中,以原子4为基础,选出了1和5,放入到不同的候选集中。这样,我们在第二次迭代中就产生了4个包含不同原子的候选集,重复上述步骤,直到达到稀疏度K为止。

上图为MMP-BF的算法步骤,从算法步骤可以看出,当迭代停止的时候,算法会产中很多候选集,每个候选集中的原子数均为K个,我们会在所有候选集中选出残差最小的一个作为我们最终的支撑集,这比单个候选集的原子选择模式精度更高。
但是上述算法有个很大的问题,就是随着迭代次数的增加,产生的候选集是指数增加的,即使每个节点产生两个子节点,当K比较大的时候,迭代停止时我们拥有的候选集个数是2^K个,这个数量级的计算复杂度在实际中显然不适用。
为了解决上述问题,作者提出了基于深度优先的MMP-DF算法

算法操作图如上图所示,我们先对一个候选集进行原子填充,填充的顺序遵循下面的公式
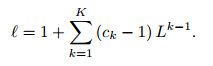

如给出L=2,K=4,则我们有16个候选集。对于第一个候选集,遵循的次序为(1,1,1,1),意思是我们在每次迭代都选出最优的原子放入候选集。而对于次序(2,1,1,1),意思是第一次迭代的时候选出次优的原子放入候选集,第二次迭代选出最优的原子放入候选集,次序中数字代表了当前迭代中所选原子是第几优的。
算法步骤如下:

基于深度优先的选择模式对于每个候选集,可以一次性的将原子选完,不进行原子的分裂和遍历。由于每次迭代所选用的内积准则未必是最优准则,同时贪婪算法所取得也是每次迭代的最优解,而不是整体最优解,所以根据次序进行原子选择的规则一定程度上可以提高获取最优解的概率。因为当前最优的原子未必是下次迭代最优的原子。
此外,为了避免计算复杂度的剧增,文章中也限制了候选集的数量,不管是MMP-DF算法还是MMP-BF算法,最大的候选集数量均设置为50。


上图仿真了无噪环境的ERR和有噪环境的MSE

从运行时间上可以看出,MMP-DF算法相较于MMP-BF算法单次迭代的运行时间减少了很多。
改进思路:
广度优先和深度优先的搜索策略属于比较传统的搜索策略,如何确定更优的搜索策略且更贴近于贪婪算法的计算框架是一个可以优化的方向。其次,如何进行剪枝,来减少MMP算法的计算复杂度也是值得考究的问题。可以从这两个方面入手,和之前的一些阈值策略,选择策略等结合。
这篇关于压缩感知重构算法--MMP-BF和MMP-DF算法及其改进思路的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








