《Modern Robotics》阅读笔记6—

本文主要是介绍《Modern Robotics》阅读笔记6——前向运动学，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

《Modern Robotics》阅读笔记6——前向运动学

前向运动学（Forward Kinematics）是《Modern Robotics》一书的第三章，这章主要介绍的内容就是如何基于旋量理论使用PoE（Product of Exponentials）形式求解机器人的前向运动学。有了之前对于旋量理论的了解，这一章的内容非常简单。

前向运动学：描述的是从关节角（关节平移）到机器人末端位姿的映射关系。也就是从部分运动映射到整体运动的关系。

接下来，就以两个例子来介绍前向运动学的求解过程。第一个例子，旋量是表示在固定系{s}下的。第二个例子，旋量表示在末端坐标系{b}下。

例1：旋量轴表达在固定系下

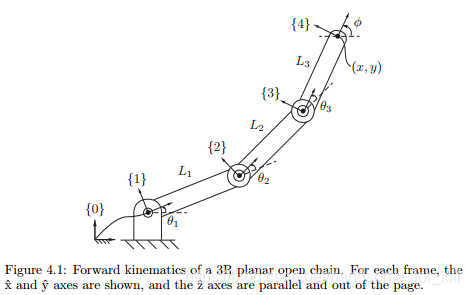
在这里插入图片描述

这是一个具有3个旋转关节的在平面范围内运动的机械臂。图中，我们定义了坐标系{0}，{1}，{2}，{3}，{4}。其中，x轴沿着连杆方向，y轴与连杆方向垂直，z轴与转轴方向共线。

求解该机械臂的前向运动学，也就是求解每个关节角度 $[\theta_1,\theta_2,\theta_3]$ 与末端坐标系{4}的关系。

D-H方法

对于这个问题，首先，我们可以用经典的D-H方法做个示范。
$T_{04}=T_{01} T_{12} T_{23} T_{34}$
其中：
$T_{01}=\left[\begin{array}{cccc}{\cos \theta_{1}} & {-\sin \theta_{1}} & {0} & {0} \\ {\sin \theta_{1}} & {\cos \theta_{1}} & {0} & {0} \\ {0} & {0} & {1} & {0} \\ {0} & {0} & {0} & {1}\end{array}\right], \quad T_{12}=\left[\begin{array}{ccc}{\cos \theta_{2}} & {-\sin \theta_{2}} & {0} & {L_{1}} \\ {\sin \theta_{2}} & {\cos \theta_{2}} & {0} & {0} \\ {0} & {0} & {1} & {0} \\ {0} & {0} & {0} & {1}\end{array}\right]$
$T_{23}=\left[\begin{array}{ccc}{\cos \theta_{3}} & {-\sin \theta_{3}} & {0} & {L_{2}} \\ {\sin \theta_{3}} & {\cos \theta_{3}} & {0} & {0} \\ {0} & {0} & {1} & {0} \\ {0} & {0} & {0} & {1}\end{array}\right], \quad T_{34}=\left[\begin{array}{cccc}{1} & {0} & {0} & {L_{3}} \\ {0} & {1} & {0} & {0} \\ {0} & {0} & {1} & {0} \\ {0} & {0} & {0} & {1}\end{array}\right]$
可以看到， $T_{04}$ 是一个与 $[\theta_1,\theta_2,\theta_3]$ 有关的函数。

基于旋量理论的PoE方法

基于旋量的PoE方法，最大的特点就是无需对于每一根连杆建立复杂的坐标系，只需要建立固定坐标系和末端坐标系就可以对运动进行表示了。下面对这个方法进行介绍：

第一步，我们需要定义机械臂的初始位置，这里将 $[\theta_1,\theta_2,\theta_3]$ 全为0，作为机械臂的初始姿态，也就相当于将图中的机械臂完全放平。

第二步，我们定义末端坐标系和固定坐标系，并且计算初始姿态下末端坐标系相对于固定坐标系的位姿M。这里末端坐标系就是{4}系，固定坐标系就是{1}系。初始姿态下，有：

$M=\left[\begin{array}{cccc}{1} & {0} & {0} & {L_{1}+L_{2}+L_{3}} \\ {0} & {1} & {0} & {0} \\ {0} & {0} & {1} & {0} \\ {0} & {0} & {0} & {1}\end{array}\right]$

第三步，计算旋量轴。需要注意，这里计算的旋量轴是表示在{1}系固定系下的。因此，我们从3号关节开始。假设 $\theta_1$ 和 $\theta_2$ 都等于0，对应于3号关节，其旋量轴的表示为：
$\mathcal{S}_{3}=\left[\begin{array}{c}{\omega_{3}} \\ {v_{3}}\end{array}\right]=\left[\begin{array}{c}{0} \\ {0} \\ {1} \\ {0} \\ {-\left(L_{1}+L_{2}\right)} \\ {0}\end{array}\right]$

这是怎么来的呢？

前文说到，旋量轴的六个量中，前三个量定义了旋转轴矢量的方向，而后三个量和前三个量则共同定义了旋转轴的位置。另外，旋量轴也可以理解为，固定系的原点在当前的刚体运动下的角速度和线速度。（这里主要说的是旋转关节，移动关节会有一些不同）

对于3号关节，旋转轴的方向显然指向z轴，另外我们定义角速度的模为1 rad/s，结合二者，所以 $\omega_{3}=[0,0,1]^T$ 。对于固定系{1}的原点而言，当机械臂末端绕3号关节以 $\omega_{3}=[0,0,1]^T$ 的角速度运动时，该点产生的线速度为 $v_{3}=[0,-\left(L_{1}+L_{2}\right),0]^T$ 。由此，就得到了旋量轴的表示。

于是，根据前文中介绍的刚体运动知识，我们知道当 $\theta_1=0$ 和 $\theta_2=0$ 时，有：
$T_{04}=e^{\left[S_{3}\right] \theta_{3}} M\left(\text { for } \theta_{1}=\theta_{2}=0\right)$
值得注意，这里指数表达式乘在了M的左边。（左乘是因为旋量轴表达在固定系{1}系下！）
其中：
$\left[\mathcal{S}_{3}\right]=\left[\begin{array}{cc}{[\omega]} & {v} \\ {0} & {0}\end{array}\right]=\left[\begin{array}{rrrr}{0} & {-1} & {0} & {0} \\ {1} & {0} & {0} & {-\left(L_{1}+L_{2}\right)} \\ {0} & {0} & {0} & {0} \\ {0} & {0} & {0} & {0}\end{array}\right]$

以此类推，我们计算2号关节和1号关节的旋量轴，如下：
$\mathcal{S}_{2}=\left[\begin{array}{c}{\omega_{2}} \\ {v_{2}}\end{array}\right]=\left[\begin{array}{c}{0} \\ {0} \\ {1} \\ {0} \\ {-L_{1}} \\ {0}\end{array}\right]， \mathcal{S}_{1}=\left[\begin{array}{c}{\omega_{1}} \\ {v_{1}}\end{array}\right]=\left[\begin{array}{c}{0} \\ {0} \\ {1} \\ {0} \\ {0} \\ {0}\end{array}\right]$
有：
$T_{04}=e^{\left[\mathcal{S}_{1}\right] \theta_{1}} e^{\left[\mathcal{S}_{2}\right] \theta_{2}} e^{\left[\mathcal{S}_{3}\right] \theta_{3}} M$
读者可以验证，PoE方法计算得到 $T_{04}$ 与D-H方法得到的完全一样。

值得注意的是，在这里我们是从3号关节一直算到1号关节，为什么要这么做呢？顺序倒过来可以吗？

答案是否定的，必须从3号关节算到1号关节。由于旋量轴是定义在固定系{1}系下的，假如我们首先旋转1号关节，那么2号关节和3号关节的也会运动，这样2号关节和3号关节的旋量轴的表达就与1号关节的角度有关了，这是旋量轴就不好求了，需要建立坐标系，这样也就违背了我们使用旋量计算运动学的初衷。
而当我们先计算3号关节，然后是2号，最后是1号，这样就不会有这种麻烦。因为旋转3号关节，2号和1号相对于固定系都没有任何运动，旋量轴非常直观。

例2：旋量轴表达在末端系下

还是上文中的同一个例子，现在我们把旋量轴表达在末端系下。

依然是定义初始位置，以及末端系在固定系下的表达M:
$M=\left[\begin{array}{cccc}{1} & {0} & {0} & {L_{1}+L_{2}+L_{3}} \\ {0} & {1} & {0} & {0} \\ {0} & {0} & {1} & {0} \\ {0} & {0} & {0} & {1}\end{array}\right]$

把旋量轴表达在末端系下，那么我们的计算顺序需要改变成：首先1号关节，其次2号关节，最后3号关节。

$\mathcal{B}_{1}=\left[\begin{array}{c}{\omega_{1}} \\ {v_{1}}\end{array}\right]=\left[\begin{array}{c}{0} \\ {0} \\ {1} \\ {0} \\ {L_{1}+L_{2}+L_{3}} \\ {0}\end{array}\right]， \mathcal{B}_{2}=\left[\begin{array}{c}{\omega_{2}} \\ {v_{2}}\end{array}\right]=\left[\begin{array}{c}{0} \\ {0} \\ {1} \\ {0} \\ {L_{2}+L_{3}} \\ {0}\end{array}\right]， \mathcal{B}_{3}=\left[\begin{array}{c}{\omega_{3}} \\ {v_{3}}\end{array}\right]=\left[\begin{array}{c}{0} \\ {0} \\ {1} \\ {0} \\ {L_3} \\ {0}\end{array}\right]$