LeetCode——贪心思想（455. 分发饼干、435. 无重叠区间、452. 用最少数量的箭引爆气球、406. 根据身高重建队列、122|123.买卖股票的最佳时机、605. 种花问题...）

一、455. 分发饼干

1.1 题目描述

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。（难度:简单）

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

 示例 1:输入: g = [1,2,3], s = [1,1]
            输出: 1

解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

示例 2:输入: g = [1,2], s = [1,2,3]
            输出: 2

解释: 
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

1.2 代码

1.2.1 排序+贪心

思想：

为了了满足更多的小孩，就不要造成饼干尺寸的浪费。大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子，那么就应该优先满足胃口大的。

这里的局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。

可以尝试使用贪心策略，先将饼干数组和小孩数组排序。然后从后向前遍历小孩数组，用大饼干优先满足胃口大的，并统计满足小孩数量。

package GreedyThought;import java.util.Arrays;/*** @author : lkw* @data : 2021/3/22 9:51* @description :455. 分发饼干(简单)**/
public class findContentChildren_01 {public static void main(String[] args) {int g[] = {1,2,3,5};int s[] = {1,2,7};findContentChildren(g,s);}public static int findContentChildren(int[] g, int[] s) {int sum=0;Arrays.sort(g);Arrays.sort(s);int star=0;for (int i = 0; i < g.length;i++ ) {for (int j=star; j < s.length; j++) {if (s[j]>=g[i]){star=j+1;sum=sum+1;break;}}}System.out.println(sum);return sum;}
}

 

package GreedyThought;import java.util.Arrays;/*** @author : lkw* @data : 2021/3/22 10:17* @description :455. 分发饼干(简单)* 精简上一个代码**/
public class findContentChildren_02 {public static void main(String[] args) {int g[] = {1,2,3,5};int s[] = {1,2,7};findContentChildren(g,s);}public static int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int child=0;int cookie=0;while (child<g.length && cookie< s.length){if (s[cookie]>=g[child]){child++;}cookie++;}
return child;}
}

 

二、435. 无重叠区间

1.1 题目描述

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

注意:可以认为区间的终点总是大于它的起点。区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。

示例 1:输入: [ [1,2], [2,3], [3,4], [1,3] ]

输出: 1

解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例 2:输入: [ [1,2], [1,2], [1,2] ]

输出: 2

解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

示例 3:输入: [ [1,2], [2,3] ]

输出: 0

解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

1.2 代码

1.2.1 贪心算法

贪心算法，按照起点排序：选择结尾最短的，后面才可能连接更多的区间（如果两个区间有重叠，应该保留结尾小的） 把问题转化为最多能保留多少个区间，使他们互不重复，则按照终点排序，每个区间的结尾很重要，结尾越小，则后面越有可能容纳更多的区间。

思路：https://leetcode-cn.com/problems/non-overlapping-intervals/solution/wu-zhong-die-qu-jian-ji-bai-liao-100de-y-kkzr/

Lambda表达式：接收2个参数(数字),并返回他们的差值 (x, y) -> x – y

小顶堆的比较器：(a, b) -> a - b

大顶堆的比较器：(a, b) -> b - a

此题，按头升序的比较器：(a, b) -> a[0] - b[0]

package GreedyThought;import java.util.ArrayList;
import java.util.Arrays;/*** @author : lkw* @data : 2021/3/22 10:27* @description :435. 无重叠区间(难度中等)**/
public class eraseOverlapIntervals_01 {public static void main(String[] args) {//int intervas[][]={{1,2},{2,3},{3,4},{1,3}};int intervas[][]={{1,2},{1,2},{1,2}};//int intervas[][]= {{1,100},{11,22},{1,11},{2,12}};eraseOverlapIntervals(intervas);}public static int eraseOverlapIntervals(int[][] intervals) {if (intervals.length==0)return 0;Arrays.sort(intervals, (a, b) -> a[0] - b[0]);//按头的升序排的
//        for (int i = 0; i < intervals.length; i++) {
//            System.out.println(Arrays.toString(intervals[i]));
//        }//记录区间尾部的位置int end= intervals[0][1];int count =0;//统计重叠的个数for (int i = 1; i < intervals.length; i++) {if(intervals[i][0]<end){//如果重叠了肯定是要移除一个的，因此count++//然后更新尾部，保留较小的尾部count++;end = Math.min(end,intervals[i][1]);}else{//如果没有重叠，不需要移除，现在只需要更新区间尾部的位置end= intervals[i][1];}}System.out.println(count);return  count;}}

 

 

三、452. 用最少数量的箭引爆气球

3.1 题目描述

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以纵坐标并不重要，因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。(难度中等)

一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足  xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

给你一个数组 points ，其中 points [i] = [xstart,xend] ，返回引爆所有气球所必须射出的最小弓箭数。

 
示例 1：输入：points = [[10,16],[2,8],[1,6],[7,12]]
          输出：2

解释：对于该样例，x = 6 可以射爆 [2,8],[1,6] 两个气球，以及 x = 11 射爆另外两个气球

示例 2：输入：points = [[1,2],[3,4],[5,6],[7,8]]
          输出：4

示例 3：输入：points = [[1,2],[2,3],[3,4],[4,5]]
          输出：2

示例 4：输入：points = [[1,2]]
          输出：1

示例 5：输入：points = [[2,3],[2,3]]
          输出：1

提示：0 <= points.length <= 104
           points[i].length == 2
          -231 <= xstart < xend <= 231 - 1

 

3.2 代码

3.2.1 贪心+排序

思路：用区间的尾部排序貌似效率会更好, 因为已经保证后面的区间右侧都是大于当前区间, 所以将发射点设置在右侧边界, 后面的区间只有左边界比它更靠左,则可以被一起处理掉。
这里换个example: [[10,16],[2,5],[1,6],[7,12]] 为例子:

先排序, 按区间结束位置排序, 排序后: [[2,5],[1, 6],[7,12],[10,16]]

遍历计算交叉区间,

1. 发射点初始化为pos = 5, 需要的箭数量 arrows = 1;
2. 区间[1, 6], 1 是小于5的, 在点5射箭可以干掉这个区间
3. 区间[7, 12], 在5的位置射箭无法打掉, 说明需要增加一个新的发射点, 新的待发射点pos = 12
4. 区间[10,16], 10 < 12那么在12位置射箭可以干掉它
5. 返回需要射击点数量

思路：https://leetcode-cn.com/problems/minimum-number-of-arrows-to-burst-balloons/solution/he-bing-qu-jian-lei-de-ti-mu-du-shi-yi-ge-tao-lu-a/

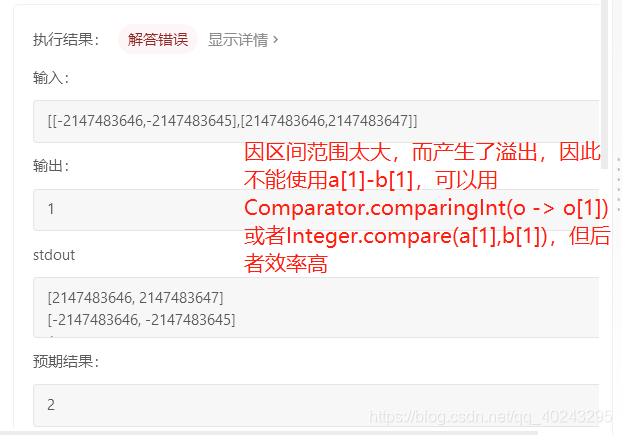
package GreedyThought;import java.util.Arrays;/*** @author : lkw* @data : 2021/3/23 9:51* @description :452. 用最少数量的箭引爆气球(难度中等)* **/
public class findMinArrowShots_01 {public static void main(String[] args) {//int points[][]={{10,16},{2,8},{1,6},{7,12}};//2//int points[][]={{1,2},{3,4},{5,6},{7,8}};//4//int points[][]={{1,2},{2,3},{3,4},{4,5}};//2//int points[][]={{2,3},{2,3}};//1//int points[][]={{9,12},{1,10},{4,11},{8,12},{3,9},{6,9},{6,7}};int points[][]={{-2147483646,-2147483645},{2147483646,2147483647}};findMinArrowShots(points);}public static int findMinArrowShots(int[][] points) {if (points.length==0) return 0;/*此用例int points[][]={{-2147483646,-2147483645},{2147483646,2147483647}};因区间范围太大，而产生了溢出，因此sort不能使用a[1]-b[1]，可以用Comparator.comparingInt(o -> o[1])或者Integer.compare(a[1],b[1])，但后者效率高*///Arrays.sort(points, (a, b)->a[1]-b[1]);//Arrays.sort(points, Comparator.comparingInt(o -> o[1]));//按尾部升序排列Arrays.sort(points, (a, b)->Integer.compare(a[1],b[1]));//按尾部升序排列// for (int i = 0; i < points.length; i++) {//   System.out.println(Arrays.toString(points[i]));//}int end = points[0][1];int arrow =1;for (int i = 1; i < points.length; i++) {if (points[i][0]<=end){//满足if说明此区间的左端点，在end的左侧，又因为是按照后端点升序排列的，说明有重叠区域，从end发射可以都射中//可以穿透，则不需要修改变量continue;}else {//说明区间不重叠，则重选添加一个arrow的位置，位置为points[i][1]arrow++;end=points[i][1];}}//System.out.println(arrow);return  arrow;}
}

 

四、406. 根据身高重建队列

4.1 题目描述

假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面 正好 有 ki 个身高大于或等于 hi 的人。

请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性（queue[0] 是排在队列前面的人）。

示例 1：输入：people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]

解释：
编号为 0 的人身高为 5 ，没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ，没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ，有 2 个身高更高或者相同的人排在他前面，即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
编号为 4 的人身高为 4 ，有 4 个身高更高或者相同的人排在他前面，即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。

示例 2：输入：people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出：[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]

4.2 代码

解题思路：先排序再插入

1.排序规则：按照先H身高降序，K个数升序排序。

2.遍历排序后的数组，根据K插入到K的位置上

核心思想：高个子先站好位，矮个子插入到K位置上，前面肯定有K个高个子，矮个子再插到前面也满足K的要求

思路：https://leetcode-cn.com/problems/queue-reconstruction-by-height/solution/406-gen-ju-shen-gao-zhong-jian-dui-lie-java-xian-p/

 Arrays.sort(people, (a, b) -> a[0] == b[0] ? (a[1] - b[1]) : (b[0] - a[0]));//先按身高a[0]降序排，再按k升序排
//a,b表示的是两个对象，身高是第一位a[0],k是第二位a[1]
//代码含义：若身高相等，则升序排k，若身高不相等，则降序排身高。

package GreedyThought;import java.util.ArrayList;
import java.util.Arrays;/*** @author : lkw* @data : 2021/3/23 14:11* @description :406. 根据身高重建队列**/
/*
最开始的思考：按尾部升序排列
比较首部，若小则往前移（但是如何存储，怎么插入？ 固定数组，指定坐标移）
插入使用ArrayList*/
public class reconstructQueue_01 {public static void main(String[] args) {int people[][] = {{7, 0}, {4, 4}, {7, 1}, {5, 0}, {6, 1}, {5, 2}};int num[][]= reconstructQueue(people);for (int i = 0; i < people.length; i++) {System.out.println(Arrays.toString(num[i]));}}public static int[][] reconstructQueue(int[][] people) {//如果不是一个数组，即先让高个站好，在根据k将小个子插入
//        for (int i = 0; i < people.length; i++) {
//            System.out.println(Arrays.toString(people[i]));
//        }if (people.length==0 && people==null) return people;//1.先排序Arrays.sort(people, (a, b) -> a[0] == b[0] ? (a[1] - b[1]) : (b[0] - a[0]));//先按身高降序排，再按k升序排ArrayList<int[]> array = new ArrayList<>();//2.将低个子插入k的位置for (int[]p: people){//System.out.println(Arrays.toString(p)); //每次输出people[i]array.add(p[1],p);//把p插入p[1]位置,p[1]就是k值}return array.toArray(new int[array.size()][]);}
}

 

4.3 补充：数组的三种比较的 ==，a.equals(b)，和Arrays.equals(a,b)

若a，b都为数组，则：

• a=b ，比较的是地址
• a.equals(b) 比较的是地址
• Arrays.equals(a, b) 比较的是元素内容

原因：

int没有定义equals，而Object类中的equals方法是用来比较“地址”的。

数组a==数组b，比较的是地址，两个变量的内存地址不一样，也就是说它们指向的对象不 一样。 

当比较两个字符串的时候，它使用的是String类下的equals()方法，这个方法比较的是元素内容。

当比较两个数组的值的时候，需要使用Arrays类中的equals()方法。即Arrays.equals(a, b)；

package GreedyThought;import org.w3c.dom.ls.LSOutput;import java.util.Arrays;/*** @author : lkw* @data : 2021/3/23 14:52* @description :数组的三种比较的 ==，a.equals(b)，和Arrays.equals(a,b)**//*
若a，b都为数组，则：a=b ，比较的是地址a.equals(b) 比较的是地址Arrays.equals(a, b) 比较的是元素内容当比较两个字符串的时候，它使用的是String类下的equals()方法，这个方法比较的是对象值。
当比较两个数组的值的时候，需要使用Arrays类中的equals()方法。即Arrays.equals(a, b)*/public class pra {public static void main(String[] args) {int a[] = {1, 2, 3, 4};int b[] = {1, 2, 3, 4};System.out.println(a.equals(b));//false，int没有定义equals，而Object类中的equals方法是用来比较“地址”的，所以等于false.System.out.println(a == b);//false，两个变量的内存地址不一样，也就是说它们指向的对象不 一样，System.out.println(Arrays.equals(a, b));//true,比较的是元素内容String c= "lalal";String d= "lalal";System.out.println(c.equals(d));//true,比较的数值}
}

 

五、121. 买卖股票的最佳时机

5.1 题目描述

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择某一天买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：输入：[7,1,5,3,6,4]
              输出：5
              解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
                      注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：输入：prices = [7,6,4,3,1]
              输出：0
              解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

 

5.2 代码

5.2.1 暴力（超时）

最简单的思想，但是超出了时间限制

  //超出时间限制public static int maxProfit(int[] prices) {int diff= 0;for (int i = 0; i < prices.length-1; i++) {for (int j = i; j < prices.length; j++) {if (prices[j]-prices[i]>diff)diff=prices[j]-prices[i];}}System.out.println(diff);return diff;}

 

5.2.1 动态规划

DP 动态规划(dynamic programming)

DP的思路： 利用原问题与子问题的关系，将其变成大问题的解 = 小问题的解的函数， 从而将问题变成size的扩展即可，当size到达最大后，原问题解决了。

1.大问题与小问题的关系

   1）状态定义：我们定义diff为第i天的最大利润
   2）状态转移方程：
      第i天的最大收益和第i-1天的最大收益之间的关系：
          i) 最大收益不是第i天抛出的    ——最大收益和第i天的价格无关
         ii) 最大收益是在第i-1天前某天买入的，并在第i天抛出的——与第i天的价格有关

     因此第i天的最大收益等于：第i天抛出所造成的最大收益 和 第i-1天之前的最大收益 中的最大值，即：
     前i天的最大收益 = max{前i-1天的最大收益，第i天的价格-前i-1天中的最小价格}
     其中： 前i-1天中的最小价格需时时更新并记录

2.初始条件：min 和 diff

•  min可以等于第一天的price
•  diff利润可以等于0， 因为最大收益的最小值就是0。

3.小于最小问题的特殊情况： 当list的长度为0 和 1 时， 没有办法带入转移公式中，需要特殊处理。

此题思路：

1. 记录【今天之前买入的最小值】
2. 计算【今天之前最小值买入，今天卖出的获利】，也即【今天卖出的最大获利】
3. 比较【每天的最大获利】，取最大值即可

即记录前面的最小值，将此最小值作为买入价格，然后将当前价格作为卖出价格，计算利润是否最大。（贪心思想：当前最优）

package GreedyThought;/*** @author : lkw* @data : 2021/3/24 10:25* @description :121.maxProfit(easy)* 记录之前的最小值作为买入价格* 记录当前价格为卖出价格* 计较此时利润是否最大**///贪心思想，当前最优
public class maxProfit_02 {public static void main(String[] args) {int[] prices = {7,1,5,3,6,4};maxProfit(prices);}public static int maxProfit(int[] prices) {if (prices.length<=1) return 0;int min= prices[0];//记录最小值int diff= 0;//利润for (int i = 1; i < prices.length; i++) {if (prices[i]<min) min = prices[i];//修改最小值else diff = Math.max(prices[i]-min,diff);}System.out.println(diff);return diff;}
}

复杂度分析

• 时间复杂度：O(n)，只需要遍历一次。
• 空间复杂度：O(1)，只使用了常数个变量。

 

六、122. 买卖股票的最佳时机 II

6.1 题目描述

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:输入: [7,1,5,3,6,4]
输出: 7解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
          随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
        注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
         因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

 

6.2 代码

6.2.1 贪心算法

 题目的意思是第三天卖出第三天不能再买入了。因为第二天到第四天一直再涨，所以第二天买第四天卖这样使得利润最大。因此可以简化为只要今天比昨天大，就卖出。{7,1,5,3,6,4}这种数组可以这样理解。

但{1, 2, 3, 4, 5, 6}这种数组，存在疑惑（如果不是今天卖掉，今天买，就不能用此种方法计算了）

贪心算法，思想简化为：只要今天价格大于昨天的价格就在今天卖出。

看到下面的解题思路，解出了我的困惑：原来不可以同一天买卖，只是将连续上涨的情况也可用此公式表达。

题解：https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/solution/best-time-to-buy-and-sell-stock-ii-zhuan-hua-fa-ji/

package GreedyThought;/*** @author : lkw* @data : 2021/3/24 11:02* @description :122. 买卖股票的最佳时机 II* 贪心算法，一次遍历，只要今天价格大于昨天的价格就在今天卖出* 
持续上涨的情况只是可以用此式子表达，不是代表可以当天同时买卖**/
public class maxProfit2_01 {public static void main(String[] args) {int[] prices = {1, 2, 3, 4, 5, 6};maxProfit(prices);}public static int maxProfit(int[] prices) {int diff = 0;if (prices.length <= 0) return 0;for (int i = 1; i < prices.length; i++) {if (prices[i] > prices[i - 1]) {diff = diff + prices[i] - prices[i - 1];}}return diff;}
}

时间复杂度：O(n),遍历一遍数组

空间复杂度：O(1)，创建了常数个变量

 

七、605. 种花问题

7.1 题目描述

假设有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花不能种植在相邻的地块上，它们会争夺水源，两者都会死去。

给你一个整数数组  flowerbed 表示花坛，由若干 0 和 1 组成，其中 0 表示没种植花，1 表示种植了花。另有一个数 n ，能否在不打破种植规则的情况下种入 n 朵花？能则返回 true ，不能则返回 false。

示例 1：输入：flowerbed = [1,0,0,0,1], n = 1
输出：true

示例 2：输入：flowerbed = [1,0,0,0,1], n = 2
输出：false

7.2 代码

7.2.1 贪心思想

从左向右遍历花坛，在可以种花的地方就种一朵，能种就种（因为在任一种花时候，不种都不会得到更优解），就是一种贪心的思想。
这里可以种花的条件是：

• 自己为空
• 左边为空 或者 自己是最左
• 右边为空 或者 自己是最右

package GreedyThought;/*** @author : lkw* @data : 2021/3/24 15:07* @description :605. 种花问题(简单)**/
public class canPlaceFlowers_01 {public static void main(String[] args) {//int[] flowerbed = {1,0,1,0,1,0,0,0};int[] flowerbed = {1,0,0,0,1};//int[] flowerbed = {0,0};int n=1;System.out.println(canPlaceFlowers(flowerbed, n));}public static boolean canPlaceFlowers(int[] flowerbed, int n) {int k=0;for(int i=0; i<flowerbed.length; i++) {if(flowerbed[i] == 0 && (i == 0 || flowerbed[i-1] == 0) //是左侧边界或者左侧为0&& (i == flowerbed.length-1 || flowerbed[i+1] == 0)) //是右侧边界或者右侧为0{k++;flowerbed[i] = 1;}}if (n>k) return false;else return true;}}

 

八、392. 判断子序列

8.1 题目描述

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。(难度简单)

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

进阶：如果有大量输入的 S，称作 S1, S2, ... , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

示例 1：输入：s = "abc", t = "ahbgdc"
输出：true

示例 2：输入：s = "axc", t = "ahbgdc"
输出：false

 

8.2 代码

8.2.1 双指针+贪心

当我们从前往后匹配，可以发现每次贪心地匹配靠前的字符是最优决策。

思路：

1.先将两个字符串转为数组形式，sc和tc两个数组，i，j分别为其下标索引。

2.若sc[ i ]==tc[ j ],说明比对上了，则此时sc和tc索引都移至下一位，进行下一位的比较。

3.若不等于，则说明没有比对上，则只移动tc的索引j，若tc都移至最后一位，还为比对上，则sc不是tc的字符串。

  若sc索引为s.length()则说明比对上了（因为若最后一位比对上了，还有i++，因为为s.length()）

将数组长度记为m，n后，以后每次循环不需要再计算长度，这样提高执行时间提高了很多。 

package GreedyThought;/*** @author : lkw* @data : 2021/3/25 8:32* @description :392. 判断子序列(难度简单)* 贪心+双指针**/
public class isSubsequence_01 {public static void main(String[] args) {//String s = "axc", t = "ahbgdc";String s = "abc", t = "ahbgdc";System.out.println(isSubsequence(s, t));}public static boolean isSubsequence(String s, String t){char[] sc= s.toCharArray();char[] tc= t.toCharArray();int i,j;int m=s.length();int n=t.length();for (i = 0,j=0; i < m && j<n; ) {if (sc[i]==tc[j]){i++;j++;}else j++;}//            if (i==m){
//                return true;
//            }
//            else return false;return i==m;}}

• 时间复杂度：O(n) ,最差情况下循环遍历一遍数组t。
• 空间复杂度：O(n+m) ，构建了两个数组，sc和tc。

 

为了节省空间，不转数组了，使用s.charAt(i)，取s的第i位。

package GreedyThought;/*** @author : lkw* @data : 2021/3/25 8:59* @description :392. 判断子序列(难度简单)* 优化空间复杂度* 将长度赋值给m，m=s.length()，之后使用到后调用m，比每次计算长度省很多时间**/
public class isSubsequence_02 {public static void main(String[] args) {//String s = "axc", t = "ahbgdc";String s = "abc", t = "ahbgdc";System.out.println(isSubsequence(s, t));}public static boolean isSubsequence(String s, String t){int i=0,j=0;int m=s.length();int n=t.length();while(i<m && j<n){if (s.charAt(i)==t.charAt(j)){i++;j++;}else j++;}//return (i==s.length())?true:false;return i==m;}
}

• 时间复杂度：O(n)，循环最大的字符串长度，因为i与j同时移动，且m<n,时间复杂度O(max(m,n))
• 空间复杂度：O(1)

 

九、665. 非递减数列

9.1题目描述

给你一个长度为 n 的整数数组，请你判断在 最多 改变 1 个元素的情况下，该数组能否变成一个非递减数列。

我们是这样定义一个非递减数列的： 对于数组中任意的 i (0 <= i <= n-2)，总满足 nums[i] <= nums[i + 1]。

示例 1:输入: nums = [4,2,3]
输出: true
解释: 你可以通过把第一个4变成1来使得它成为一个非递减数列。

示例 2:输入: nums = [4,2,1]
输出: false
解释: 你不能在只改变一个元素的情况下将其变为非递减数列。

9.2 代码

9.2.1 贪心思想

采取贪心的策略，在遍历时，每次需要看连续的三个元素，也就是瞻前顾后，遵循以下两个原则：

需要尽可能不放大nums[i + 1]，这样会让后续非递减更困难；

如果缩小nums[i]，但不破坏前面的子序列的非递减性；

而且注意不用遍历完，只要修改次数大于1了，就可退出了

//举例帮助理解
3,4,2,5; 因为2<4,2<3,只能改2，因为2大于3。若2为a[i]，则a[i]=a[i-1]
1,4,2,5; 因为2<4,但2>1,则可以改2，可以改4，但建议改4，因为不知道2后面的值多大，则建议把4改小，若2为a[i]，则a[i-1]=a[i]=2
以上两个都是num[i]<num[i-1],但是一个num[i]>=num[i-2]，一个是num[i]<num[i-2]
若i==1，也修改a[i-1]=a[i];将前面的值改小if (num[i]<num[i-1]){if (i==1 || num[i]>=num[i-2]){//则将i-1修改小num[i-1]=num[i];}else {//只能修改inum[i]=num[i-1]}}
即在出现 nums[i] < nums[i - 1] 时，需要考虑的是应该修改数组的哪个数，
使得本次修改能使 i 之前的数组成为非递减数组，并且 不影响后续的操作 。
优先考虑令 nums[i - 1] = nums[i]，因为如果修改 nums[i] = nums[i - 1] 的话，
那么 nums[i] 这个数会变大，就有可能比 nums[i + 1] 大，从而影响了后续操作。
还有一个比较特别的情况就是 nums[i] < nums[i - 2]，
修改 nums[i - 1] = nums[i] 不能使数组成为非递减数组，只能修改 nums[i] = nums[i - 1]。

帮助理解： https://leetcode-cn.com/problems/non-decreasing-array/solution/3-zhang-dong-tu-bang-zhu-ni-li-jie-zhe-d-06gi/

package GreedyThought;/*** @author : lkw* @data : 2021/3/25 9:33* @description :665. 非递减数列(难度简单)**/
public class checkPossibility_01 {public static void main(String[] args) {//int num[]= {4,2,3};//ture 4变为1//int num[]= {4,2,1};//falseint num[]= {3,4,2,3};//falseSystem.out.println(checkPossibility(num));}public static  boolean checkPossibility(int[] nums) {int k=0;for (int i = 1; i < nums.length; i++) {if (nums[i]<nums[i-1]){if (i==1 ||nums[i]>=nums[i-2] ){//则修改i-1nums[i-1]=nums[i];}else {//只能修改inums[i]=nums[i-1];}if (++k>1) return false;}}return true;}
}

 

十、53. 最大子序和

10.1 题目描述

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例 1：输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：输入：nums = [1]
输出：1

示例 3：输入：nums = [0]
输出：0

示例 4：输入：nums = [-1]
输出：-1

示例 5：输入：nums = [-100000]
输出：-100000

10.2 代码

10.2.1 贪心思想

• 首先对数组进行遍历，当前子序列和为cur，最大值结果为 max
• 若当前和cur大于零，则保留前面的值。
• 若当前和cur小于0，则舍弃之前的和，重新记录cur为现在的值
• 每次比较cur和max 的大小，将最大值赋给max，遍历结束返回结果max。

简单来说：max存储和的最大值，cur只管往后加，变成负数就不继续加了，转而指向下一个数，然后重复同样的步骤往后加。

题解：https://leetcode-cn.com/problems/maximum-subarray/solution/hua-jie-suan-fa-53-zui-da-zi-xu-he-by-guanpengchn/

package GreedyThought;/*** @author : lkw* @data : 2021/3/25 16:28* @description :53. 最大子序和(难度简单)**/
public class maxSubArray_02 {public static void main(String[] args) {int[] nums = {-2,1,-3,4,-1,2,1,-5,4};maxSubArray(nums);}public static int maxSubArray(int[] nums) {int cur=nums[0];//记录当前值int max = nums[0];记录当前最大值,初始化为第一个元素的值，若数组只一个值并且为负，记为0就不正确了int len =nums.length;for (int i = 1; i < len; i++) {if (cur>0){//若当前和大于零，则保留前面的值cur= cur+nums[i];}else {//若小于0，则舍弃之前的和，重新记录cur为现在的值cur =nums[i];}max= Math.max(cur,max);//比较当前和与之前的最大值}return max;}
}

 

十一、763. 划分字母区间

11.1 题目描述

字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。

（难度中等）

示例：输入：S = "ababcbacadefegdehijhklij"
输出：[9,7,8]
解释：
划分结果为 "ababcbaca", "defegde", "hijhklij"。
每个字母最多出现在一个片段中。像 "ababcbacadefegde", "hijhklij" 的划分是错误的，因为划分的片段数较少。
 

提示：S的长度在[1, 500]之间。S只包含小写字母 'a' 到 'z' 。

 

11.2 代码

11.2.1贪心思想

在得到每个字母最后一次出现的下标位置之后，可以使用贪心的方法将字符串划分为尽可能多的片段，思路如下：

1. 先记录每个单词出现的最后位置，数组last[26]
2. 假设第一个a最后出现的位置为8，在循环到8之前，还会循环到别的字母，若别的字母的结束位置大于8，则将此结束位置替换当前end，继续遍历。
3. 如果当前循环位置i=end，则从此位置断开

注意：end取值时，只取有值的地方，提高效率

即end =Math.max(end,last[S.charAt(i)-'a']);//end取值时：last[S.charAt(i)-'a']只取当前元素出现的最终位置，没有遍历last数组为0的位置。

package GreedyThought;import java.util.ArrayList;
import java.util.List;/*** @author : lkw* @data : 2021/3/26 8:30* @description :763. 划分字母区间（难度中等）**/
public class partitionLabels_01 {public static void main(String[] args) {//String S= "ababcbacadefegdehijhklij";String S= "efghejjiijhhhj";partitionLabels(S);}public static List<Integer> partitionLabels(String S) {
/*1.先记录每个单词出现的最后位置.数组，last[26]
2.第一个a最后出现的位置为8，在循环到8之前，就会循环到别的字母，如果循环到8之前，别的字母的结束位置大于8，则将此结束位置替换当前end，继续遍历。
3.如果当前循环位置i=end，则从此位置断开*/int len = S.length();int[] last = new int[26];//记录单词最终位置for (int i = 0; i <len ; i++) {last[S.charAt(i)-'a']=i;}List<Integer> list = new ArrayList();int end=0;int start=0;for (int i = 0; i < len; i++) {end =Math.max(end,last[S.charAt(i)-'a']);//last[S.charAt(i)-'a']也只循环last数组中有值的位置，0的地方没有变量if (i==end){//如果等于，则从此位置断开list.add(end-start+1);start=end+1;}}System.out.println(list);return list;}
}