缓存淘汰算法LRU-K，2Q（Two queues）

1.LRU-K

1.1 简介

LRU-K中的K代表最近使用的次数，LRU可以当作LRU-1。LRU-K主要目的是为了解决LRU算法的缓存污染问题。

什么是缓存污染？

当数据访问次数非常少，甚至只会被访问一次，数据服务完访问请求后还继续留在缓存中，白白占用缓存空间，这就是缓存污染。

1.2 原理

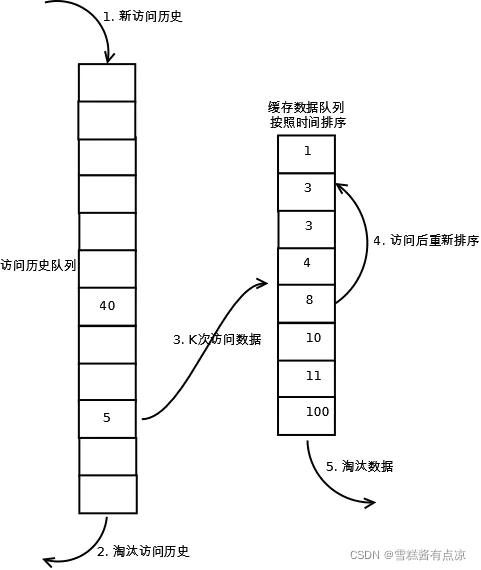
相比LRU，LRU-K除了缓存队列还要维护一个访问历史队列，这个队列不缓存数据，仅记录数据的历史访问次数。当数据访问次数达到k次时，数据才放入缓存队列。历史队列、缓存队列的维护与LRU中缓存队列的维护一样，遵循LRU原则。

1.3 过程

(1). 数据第一次被访问，加入到访问历史列表；

(2). 如果数据在访问历史列表里后没有达到K次访问，则按照一定规则（FIFO，LRU）淘汰；

(3). 当访问历史队列中的数据访问次数达到K次后，将数据索引从历史队列删除，将数据移到缓存队列中，并缓存此数据，缓存队列重新按照时间排序；

(4). 缓存数据队列中被再次访问后，重新排序；

(5). 需要淘汰数据时，淘汰缓存队列中排在末尾的数据，即：淘汰“倒数第K次访问离现在最久”的数据。

LRU-K具有LRU的优点，同时能够避免LRU的缺点，实际应用中LRU-2是综合各种因素后最优的选择，LRU-3或者更大的K值命中率会高，但适应性差，需要大量的数据访问才能将历史访问记录清除掉。

1.4 实现

// 直接继承我们前面写好的LRUCache
public class LRUKCache extends LRUCache {private int k; // 进入缓存队列的评判标准private LRUCache historyList; // 访问数据历史记录public LRUKCache(int cacheSize, int historyCapacity, int k) {super(cacheSize);this.k = k;this.historyList = new LRUCache(historyCapacity);}@Overridepublic Integer get(Integer key) {// 记录数据访问次数Integer historyCount = historyList.get(key);historyCount = historyCount == null ? 0 : historyCount;historyList.put(key, ++historyCount);return super.get(key);}@Overridepublic Integer put(Integer key, Integer value) {if (value == null) {return null;}// 如果已经在缓存里则直接返回缓存中的数据if (super.get(key) != null) {return super.put(key, value);;}// 如果数据历史访问次数达到上限，则加入缓存Integer historyCount = historyList.get(key);historyCount = historyCount == null ? 0 : historyCount;if (historyCount >= k) {// 移除历史访问记录historyList.remove(key);return super.put(key, value);}}
}
————————————————
版权声明：本文为CSDN博主「沙滩de流沙」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_41231928/article/details/120593579

2. 2Q (Tow Queues)

2.1 简介

2Q算法类似LRU-2，不同点在于2Q将LRU-2算法中的访问历史队列（仅作记录不缓存数据）改为FIFO缓存队列。即，2Q算法有两个缓存队列，一个FIFO队列，一个LRU队列。

2.2 原理

当数据第一次被访问时，2Q算法将数据缓存在FIFO队列中，数据被第二次访问时，从FIFO队列中移除并添加至LRU队列中，两个队列按照自己的方法淘汰数据。

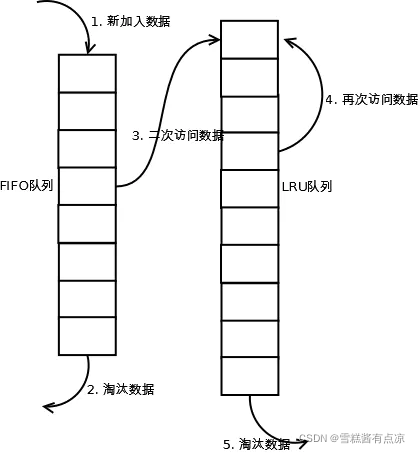
(1). 新访问的数据插入到FIFO队列；

(2). 如果数据在FIFO队列中一直没有被再次访问，则最终按照FIFO规则淘汰；

(3). 如果数据在FIFO队列中被再次访问，则将数据移到LRU队列头部；

(4). 如果数据在LRU队列再次被访问，则将数据移到LRU队列头部；

(5). LRU队列淘汰末尾的数据。

参考：
LRU-K和2Q缓存算法介绍
面试官：你知道 LRU算法 —— 缓存淘汰算法吗？