编译原理实验三：算符优先分析算法的设计与实现

2023-11-02 20:20
文章标签 算法 分析 编译 实现 设计 原理 实验 优先 算符

本文主要是介绍编译原理实验三：算符优先分析算法的设计与实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

实验三 算符优先分析算法的设计与实现

一、 实验目的
根据算符优先分析法，对表达式进行语法分析，使其能够判断一个表达式是否正确。通过算符优先分析方法的实现，加深对自下而上语法分析方法的理解。

二、 实验要求
1、输入文法。可以是如下算术表达式的文法（你可以根据需要适当改变）：

E→E+T|E-T|T
T→T*F|T/F|F
F→（E）|i

2、对给定表达式进行分析，输出表达式正确与否的判断。
程序输入/输出示例：

输入：1+2;
输出：正确
输入：(1+2)/3+4-(5+6/7);
输出：正确
输入：((1-2)/3+4
输出：错误
输入：1+2-3+(*4/5)
输出：错误

三、实验步骤
1、参考数据结构

char *VN=0,*VT=0;//非终结符和终结符数组
char firstvt[N][N],lastvt[N][N],table[N][N];
typedef struct   //符号对(P,a)
{char Vn;char Vt;
} VN_VT;
typedef struct  //栈
{VN_VT *top;VN_VT *bottom;int  size;
}stack;

2、根据文法求FIRSTVT集和LASTVT集
给定一个上下文无关文法，根据算法设计一个程序，求文法中每个非终结符的FirstVT 集和LastVT 集。
算符描述如下：

/*求 FirstVT 集的算法*/ 
PROCEDURE insert(P,a); 
IF not F[P,a] then   
begin  F[P,a] = true; //(P,a)进栈  
end;  
Procedure FirstVT; 
Begin 
for 对每个非终结符 P和终结符 a do F[P,a] = false 
for 对每个形如 P		a…或 P→Qa…的产生式 do 
Insert(P,a) 
while stack  非空 
begin 
栈顶项出栈，记为(Q,a) 
for  对每条形如 P→Q…的产生式 do insert(P,a) 
end; 
end.

同理，可构造计算LASTVT的算法。
3、构造算符优先分析表
依据文法和求出的相应FirstVT和 LastVT 集生成算符优先分析表。

算法描述如下：
for  每个形如 P->X1X2…Xn的产生式  do for i =1 to n-1 do begin if Xi和Xi+1都是终结符 then  Xi   =   Xi+1 if i<= n-2, Xi和Xi+2 是终结符, 但Xi+1 为非终结符 then Xi  = Xi+2 if Xi为终结符, Xi+1为非终结符 then   for FirstVT 中的每个元素 a do Xi  <  a ; if Xi为非终结符, Xi+1为终结符 then for LastVT 中的每个元素 a do a  >  Xi+1 ; end

4、构造总控程序
算法描述如下：

  stack S;k = 1;  //符号栈S的使用深度S[k] = ‘#’REPEAT把下一个输入符号读进a中；If S[k]   VT   then  j = k  else  j = k-1;While S[j] > a  doBeginRepeatQ = S[j];if  S[j-1]   VT  then  j = j-1  else   j = j-2until  S[j] < Q;把S[j+1]…S[k]归约为某个N，并输出归约为哪个符号；K = j+1;S[k] = N;end of whileif S[j] < a  or  S[j] = a  thenbegin  k = k+1; S[k] = a      endelse  error //调用出错诊察程序until a = ‘#’

5、对给定的表达式，给出准确与否的分析过程
6、给出表达式的计算结果。（本步骤可选作）

代码

#include <bits/stdc++.h>
using namespace std;//定义一个非终结符的结构体 
typedef struct{char left;//非终结符 int rcount;//右边式子数量 char right[200][200];//右边 int fvtcount;int lvtcount;char firstvt[200];//firstvt集合 char lastvt[200];//lastvt集合 
}grammar;
grammar gramSet[200];//产生式集 //变量的定义 
int gramcount=0;//产生式数量初始化 
int tersymcount=0;//终结符数量初始化 
int nontercount=0;//非终结符数量初始化 char terSymbol[200];//终结符号
char nonter[200];//非终结符号
char table[200][200];//分析表
char test[500];//要处理的字符串 map<char, bool> isfvted;//该非终结符是否已经求过其firstvt集
map<char, bool> islvted;//是否求过lastvt集 //函数的定义
void read();//读入数据 
bool judgesymbol(char ch);//判断终结符和非终结符
void symbolsort(char ch);//字符归类
void Firstvt(char sym);//求sym的first集 
void Addfvt(char sym, char ch);//firstvt(ch)并入firstvt(sym） 
void Lastvt(char sym);//求sym的lastvt集 
void Addlvt(char sym, char  ch);//lastvt(ch)并入lastvt(sym) 
void Table();//创建算符优先分析表 
void Show();//打印分析表 
void MainControl();//总控程序int main(int argc, char** argv) {cout<<"输入文法： 以'#'结束"<<endl;read();cout<<"输入串(以'#'结束)为："<<endl;cin>>test;for(int i=0;i<strlen(test);i++)//将输入的数字替换成i，便于分析 {if(test[i]>='0'&&test[i]<='9')test[i]='i';}for(int i=0;i<gramcount;i++){Firstvt(gramSet[i].left);}for(int i=0;i<gramcount;i++){Lastvt(gramSet[i].left);}cout<<endl;cout<<"FirstVT集如下："<<endl;for(int i=0;i<gramcount;i++){cout<<"FirstVT("<<gramSet[i].left<<")"<<": ";for(int j=0;j<gramSet[i].fvtcount;j++)cout<<gramSet[i].firstvt[j]<<" ";cout<<endl;}cout<<endl;cout<<"LastVT集如下："<<endl;for(int i=0;i<gramcount;i++){cout<<"LastVT("<<gramSet[i].left<<")"<<": ";for(int j=0;j<gramSet[i].lvtcount;j++)cout<<gramSet[i].lastvt[j]<<" ";cout<<endl;}cout<<endl;cout<<"算符优先分析表如下："<<endl;Table();Show();cout<<endl;cout<<"分析步骤如下："<<endl;MainControl();return 0;
}//读入数据 
void read()
{char str[100];while(1){cin>>str;if(str[0]=='#')break;gramSet[gramcount].left=str[0];symbolsort(str[0]);//处理左边 for(int i=3;i<strlen(str);i++)//右边从str[3]处开始;str的0-2位=‘E->’ {int j=0;char ter[100];while(str[i]!='|'&&str[i]!='\0'){symbolsort(str[i]);//处理右边 ter[j++]=str[i++];	}ter[j]='\0';strcpy(gramSet[gramcount].right[gramSet[gramcount].rcount],ter);gramSet[gramcount].rcount++;} gramcount++;	}
}
//判断终结符和非终结符
bool judgesymbol(char ch)
{if(ch>='A'&&ch<='Z')return false;return true;
}
//字符归类
void symbolsort(char ch)
{if(!judgesymbol(ch)){int flag=0;for (int i= 0;i<nontercount; i++){if (ch==nonter[i]){flag=1;break;//已在非终结符集中 }}if(flag==0){nonter[nontercount++]=ch;isfvted.insert(pair<char, bool>(ch, false));islvted.insert(pair<char,bool>(ch, false));}}else{int flag=0;for (int i=0;i<tersymcount; i++){if (ch==terSymbol[i]){flag = 1;break;//已在终结符集中 }}if (flag==0){terSymbol[tersymcount++]=ch;}}
}
//求FirstVT集
void Firstvt(char sym)
{int i;for(i=0;i<gramcount;i++){if(gramSet[i].left==sym)break;//找到了该非终结符的位置 } //处理每个产生式 for(int j=0;j<gramSet[i].rcount;j++){	 char ch=gramSet[i].right[j][0];//获取右部第一个字符 //字符为终结符if(judgesymbol(ch)){int flag=0;for (int n=0; n<gramSet[i].fvtcount;n++){if (gramSet[i].firstvt[n] == ch){flag = 1;//已在firstvt集中 break;}}if(flag==0){gramSet[i].firstvt[gramSet[i].fvtcount++]=ch;//把终结符加进FIRSTVT集 }	}//字符ch为非终结符else {if(ch!=sym){//还没有求过ch的firstvt集 if(!isfvted[ch])Firstvt(ch);//firstvt(ch)并入firstvt(sym） Addfvt(sym,ch);	}//P->Qa的情况 char ch1=gramSet[i].right[j][1];if(judgesymbol(ch1)){int flag=0;for (int n=0; n<gramSet[i].fvtcount;n++){if (gramSet[i].firstvt[n] == ch1){flag = 1;//已在firstvt集中 break;}}if(flag==0)gramSet[i].firstvt[gramSet[i].fvtcount++]=ch1;//把终结符加进FIRSTVT集 }}	}isfvted[sym]=true;
}
//firstvt(ch)并入firstvt(sym）  
void Addfvt(char sym,char ch)
{int s1,s2;int c1,c2;//找到sym的位置 for(s1=0;s1<gramcount;s1++){if(gramSet[s1].left==sym)break; }//找到ch的位置 for(c1=0;c1<gramcount;c1++){if(gramSet[c1].left==ch)break; }for(c2=0;c2<gramSet[c1].fvtcount;c2++){int flag=0;for(s2=0;s2<gramSet[s1].fvtcount;s2++){if(gramSet[s1].firstvt[s2]==gramSet[c1].firstvt[c2]){flag=1;break;//已存在 } 	 }//firstvt(ch)并入firstvt(sym) if(flag==0){	gramSet[s1].firstvt[gramSet[s1].fvtcount++]=gramSet[c1].firstvt[c2];}}
}
//求sym的lastvt集
void Lastvt(char sym){int i;for(i=0;i<gramcount;i++){if(gramSet[i].left==sym)break;}//处理每个产生式 for(int j=0;j<gramSet[i].rcount;j++){	 int length=strlen(gramSet[i].right[j]);int last=length-1;char ch=gramSet[i].right[j][last];//获取右部最后一个字符 //字符为终结符if(judgesymbol(ch)){int flag=0;for (int n=0; n<gramSet[i].lvtcount;n++){if (gramSet[i].lastvt[n] == ch){flag = 1;//已在lastvt集中 break;}}if(flag==0){gramSet[i].lastvt[gramSet[i].lvtcount++]=ch;//把终结符加进FIRSTVT集 }	}//字符ch为非终结符else {if(ch!=sym){//还没有求过ch的lastvt集 if(!islvted[ch])Lastvt(ch);//lastvt(ch)并入lastvt(sym) Addlvt(sym, ch);	}//P->aQ的情况 if(last!=0){char ch1=gramSet[i].right[j][last-1];//倒数第二位 if(judgesymbol(ch1)){int flag=0;for (int n=0; n<gramSet[i].lvtcount;n++){if (gramSet[i].lastvt[n] == ch1){flag = 1;//已在lastvt集中 break;}}if(flag==0)gramSet[i].lastvt[gramSet[i].lvtcount++]=ch1;//把终结符加进LASTVT集 }}		   		}	}islvted[sym]=true;}
//lastvt(ch)并入lastvt(sym) 
void Addlvt(char sym, char  ch)
{int  s1,s2;int  c1,c2;for(s1=0;s1<gramcount;s1++)//找到sym的位置 {if(gramSet[s1].left==sym)break;}for(c1=0;c1<gramcount;c1++)//找到ch的位置 {if(gramSet[c1].left==ch)break;}for(c2=0;c2<gramSet[c1].lvtcount;c2++){int flag=0;for(s2=0;s2<gramSet[s1].lvtcount;s2++){if(gramSet[s1].lastvt[s2]==gramSet[c1].lastvt[c2]){flag=1;break;}}if(flag==0)gramSet[s1].lastvt[gramSet[s1].lvtcount++]=gramSet[c1].lastvt[c2];}
}//创建分析表 
void Table()
{int row=tersymcount+2;//优先表的行数和列数 //分析表初始化table[0][0]=' ';table[0][row-1]='#';table[row-1][0]='#';table[row-1][row-1]='=';//第0行 int j=1;for(int i=0;i<tersymcount;i++)table[0][j++]=terSymbol[i];	//第0列 int k=1;for(int i=0;i<tersymcount;i++)table[k++][0]=terSymbol[i];int p;	 //开始分析，填充表的内容//对#特殊处理for(int i=1;i<row;i++) //分析#所在的一行 {for(int j=0;j<gramSet[0].fvtcount;j++){if(table[0][i]==gramSet[0].firstvt[j]){table[row-1][i]='<';break;}}}for(int i=1;i<row;i++) //分析#所在的一列 {for(int j=0;j<gramSet[0].lvtcount;j++){if(table[i][0]==gramSet[0].lastvt[j]){table[i][row-1]='>';break;}}}//遍历所有产生式 for(int g=0;g<gramcount;g++){//遍历一个非终结符的所有产生式 for(int i=0;i<gramSet[g].rcount;i++){int n=strlen(gramSet[g].right[i]);for(int j=0;j<n-1;j++){char xi=gramSet[g].right[i][j];char xi1=gramSet[g].right[i][j+1];//Xi和Xi+1都是终结符 if(judgesymbol(xi)&&judgesymbol(xi1)){for(int r=1;r<row;r++){if(table[r][0]==xi){p=r;//找到xi的位置 break;}}for(int l=1;l<row;l++){if(table[0][l]==xi1)//找到Xi+1的位置{table[p][l]='='; break;}}}if(j<n-2){char xi2=gramSet[g].right[i][j+2];if(!judgesymbol(xi1)&&judgesymbol(xi)&&judgesymbol(xi2)){for(int r=1;r<row;r++){if(table[r][0]==xi){p=r;//找到xi的位置 break;}}for(int l=1;l<row;l++){if(table[0][l]==xi2)//找到Xi+1的位置{table[p][l]='='; break;}}}}//Xi为终结符, Xi+1为非终结符if(!judgesymbol(xi1)&&judgesymbol(xi)){int pos;for(pos=0;pos<gramcount;pos++){if(gramSet[pos].left==xi1)break;}for(int r=1;r<row;r++){if(table[r][0]==xi){p=r;//找到xi的位置 （第p行第0列） break;}}for(int x=0;x<gramSet[pos].fvtcount;x++)//对于firstvt中的每一个元素 {char a=gramSet[pos].firstvt[x];for(int l=1;l<row;l++){if(table[0][l]==a)//找到a的位置（第0行第l列） {table[p][l]='<'; break;}}}}//if Xi为非终结符, Xi+1为终结符if(!judgesymbol(xi)&&judgesymbol(xi1)){int pos;for(pos=0;pos<gramcount;pos++){if(gramSet[pos].left==xi)break;}for(int r=1;r<row;r++){if(table[0][r]==xi1){p=r;//找到xi1的位置(第0行，p列） break;}}for(int x=0;x<gramSet[pos].lvtcount;x++)//对于lastvt中的每一个元素 {char a=gramSet[pos].lastvt[x];for(int l=1;l<row;l++){if(table[l][0]==a)//找到a的位置(第l行，第0列） {table[l][p]='>'; break;}}}}}}}} //展示分析表
void Show(){int row=tersymcount+2;//优先表的行数和列数 //打印表的内容for(int k=0;k<row*11;k++)cout<<"-";cout<<endl;for(int i=0;i<row;i++){for(int j=0;j<row;j++){cout<<table[i][j];for(int k=0;k<9;k++)cout<<" ";cout<<"|";}cout<<endl;for(int k=0;k<row*11;k++)cout<<"-";cout<<endl;}}//比较s和a优先级的函数 
char prio(char s,char a)
{int row=tersymcount+2;int i;int j;for(i=1;i<row;i++){if(table[i][0]==s)break;}for(j=1;j<row;j++){if(table[0][j]==a)break;}if(table[i][j]=='>')return '>';else if(table [i][j]=='<')return '<';else if(table[i][j]=='=')return '=';elsereturn 'e';} 
//总控程序
void MainControl()
{int flag=1;int row=tersymcount+2;int j;string str[100];//存储动作str[0]="预备"; char s[100];//符号栈for(int i=0;i<100;i++)s[i]='\0';int k;//符号栈的使用深度 k=0;s[k] = '#';char a;//存放输入串当前分析符号 int pos=0;//定位a的位置 int step=0;//步骤序号 cout << endl;cout<<"步骤\t符号栈\t\t\t输入串\t\t\t\t动作"<<endl;while(flag==1){cout<<step++<<"\t";//打印步骤序号cout<<s<<"\t\t\t";//打印当前符号栈 for(int i=pos;i<strlen(test);i++)//打印当前输入串 cout<<test[i];cout<<"\t\t\t\t";cout<<str[step-1]<<endl;a=test[pos];if(judgesymbol(s[k]))j=k;else j=k-1;if(prio(s[j],a)=='>'){string strkj;//要归约的式子 while(1){char q=s[j];if(judgesymbol(s[j-1]))j=j-1;elsej=j-2;if(prio(s[j],q)=='<')break;	}//把S[j+1]…S[k]归约为某个N，并输出归约为哪个符号；char N;int flag1=1;int flag2=1;int flag3;for(int K=j+1;K<=k;K++)strkj+=s[K];int max=strkj.length();//要归约式子的长度 for(int g=gramcount-1;g>=0;g--){for(int g1=0;g1<gramSet[g].rcount;g1++)//遍历某非终结符每个产生式 {string gram1=gramSet[g].right[g1];int m=gram1.length();//右部产生式的长度//右部产生式gram1与strkj需要非终结符对非终结符，终结符对终结符且终结符相等才能归约 if(max==m)//首先判断长度是否相等 {//判断一一对应关系int p;for(p=0;p<max;p++){if(judgesymbol(strkj[p]))//如果p位置是终结符，则需要相等 {if(strkj[p]==gram1[p])flag3=1;else flag3=0;} else//p位置是非终结符，则需要对应 {if(!judgesymbol(gram1[p]))flag3=1;else flag3=0;}if(flag3==0)break;} if(flag3==1) //一一对应，则可以跳出循环 {N=gramSet[g].left;flag1=0;flag2=0;}	 }if(flag2==0)break;		}if(flag1==0)break;} if(flag1==0)//说明可归约 {for(int K=j+1;K<=k;K++)//将s[j+1]...s[k]移除 s[K]='\0';k=j+1;s[k]=N;str[step]="归约"; 	}elseflag=-1;//说明不可归约，语法错误 }else if(prio(s[j],a)=='<'||prio(s[j],a)=='='){k++;s[k]=a;str[step]="移进"; pos++;}elseflag=-1;char start=gramSet[0].left;if(a=='#'&&!judgesymbol(s[k])&&k==1){cout<<step++<<"\t";//打印最后步骤cout<<s<<"\t\t\t";//打印当前符号栈 for(int i=pos;i<strlen(test);i++)//打印当前输入串 cout<<test[i];cout<<"\t\t\t\t";cout<<str[step-1]<<endl;flag=0;}	} if(flag==0)cout<<"success！表达式正确！"<<endl;else if(flag==-1)cout<<"error!表达式不正确！"<<endl;
}

结果

测试数据：
文法：

E->E+T|E-T|T
T->T*F|T/F|F
F->(E)|i
#

测试输入1：

i*i+i#

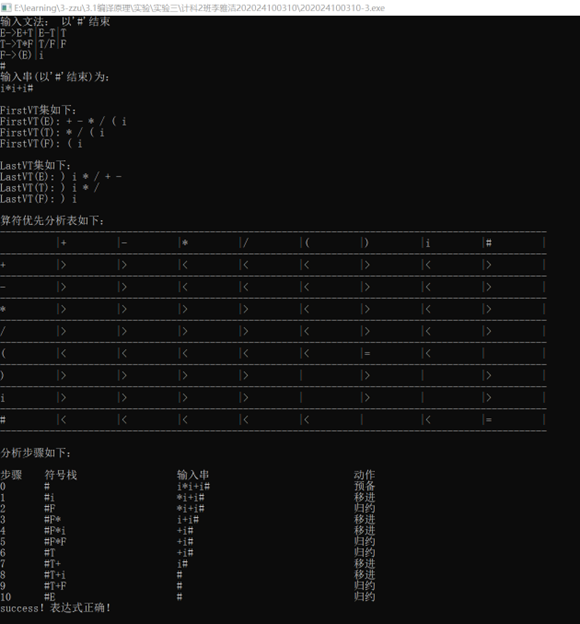
在这里插入图片描述

这篇关于编译原理实验三：算符优先分析算法的设计与实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/333078。

相关文章

SpringBoot中六种批量更新Mysql的方式效率对比分析

SpringBoot中六种批量更新Mysql的方式效率对比分析

《SpringBoot中六种批量更新Mysql的方式效率对比分析》文章比较了MySQL大数据量批量更新的多种方法,指出REPLACEINTO和ONDUPLICATEKEY效率最高但存在数据风险,MyB... 目录效率比较测试结构数据库初始化测试数据批量修改方案第一种 for第二种 case when第三种
阅读更多...
python生成随机唯一id的几种实现方法

python生成随机唯一id的几种实现方法

《python生成随机唯一id的几种实现方法》在Python中生成随机唯一ID有多种方法,根据不同的需求场景可以选择最适合的方案,文中通过示例代码介绍的非常详细,需要的朋友们下面随着小编来一起学习学习... 目录方法 1：使用 UUID 模块（推荐）方法 2：使用 Secrets 模块（安全敏感场景）方法
阅读更多...
解决1093 - You can‘t specify target table报错问题及原因分析

解决1093 - You can‘t specify target table报错问题及原因分析

《解决1093-Youcan‘tspecifytargettable报错问题及原因分析》MySQL1093错误因UPDATE/DELETE语句的FROM子句直接引用目标表或嵌套子查询导致,... 目录报js错原因分析具体原因解决办法方法一：使用临时表方法二：使用JOIN方法三：使用EXISTS示例总结报错原
阅读更多...
Spring StateMachine实现状态机使用示例详解

Spring StateMachine实现状态机使用示例详解

《SpringStateMachine实现状态机使用示例详解》本文介绍SpringStateMachine实现状态机的步骤,包括依赖导入、枚举定义、状态转移规则配置、上下文管理及服务调用示例,重点解... 目录什么是状态机使用示例什么是状态机状态机是计算机科学中的​​核心建模工具​​，用于描述对象在其生命
阅读更多...
Spring Boot 结合 WxJava 实现文章上传微信公众号草稿箱与群发

Spring Boot 结合 WxJava 实现文章上传微信公众号草稿箱与群发

《SpringBoot结合WxJava实现文章上传微信公众号草稿箱与群发》本文将详细介绍如何使用SpringBoot框架结合WxJava开发工具包,实现文章上传到微信公众号草稿箱以及群发功能,... 目录一、项目环境准备1.1 开发环境1.2 微信公众号准备二、Spring Boot 项目搭建2.1 创建
阅读更多...
IntelliJ IDEA2025创建SpringBoot项目的实现步骤

IntelliJ IDEA2025创建SpringBoot项目的实现步骤

《IntelliJIDEA2025创建SpringBoot项目的实现步骤》本文主要介绍了IntelliJIDEA2025创建SpringBoot项目的实现步骤,文中通过示例代码介绍的非常详细,对大家... 目录一、创建 Spring Boot 项目1. 新建项目2. 基础配置3. 选择依赖4. 生成项目5.
阅读更多...
Linux下删除乱码文件和目录的实现方式

Linux下删除乱码文件和目录的实现方式

《Linux下删除乱码文件和目录的实现方式》：本文主要介绍Linux下删除乱码文件和目录的实现方式,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录linux下删除乱码文件和目录方法1方法2总结Linux下删除乱码文件和目录方法1使用ls -i命令找到文件或目录
阅读更多...
MySQL中的LENGTH()函数用法详解与实例分析

MySQL中的LENGTH()函数用法详解与实例分析

《MySQL中的LENGTH()函数用法详解与实例分析》MySQLLENGTH()函数用于计算字符串的字节长度,区别于CHAR_LENGTH()的字符长度,适用于多字节字符集（如UTF-8）的数据验证... 目录1. LENGTH()函数的基本语法2. LENGTH()函数的返回值2.1 示例1：计算字符串
阅读更多...
SpringBoot+EasyExcel实现自定义复杂样式导入导出

SpringBoot+EasyExcel实现自定义复杂样式导入导出

《SpringBoot+EasyExcel实现自定义复杂样式导入导出》这篇文章主要为大家详细介绍了SpringBoot如何结果EasyExcel实现自定义复杂样式导入导出功能,文中的示例代码讲解详细,... 目录安装处理自定义导出复杂场景1、列不固定，动态列2、动态下拉3、自定义锁定行/列，添加密码4、合并
阅读更多...
mybatis执行insert返回id实现详解

mybatis执行insert返回id实现详解

《mybatis执行insert返回id实现详解》MyBatis插入操作默认返回受影响行数,需通过useGeneratedKeys+keyProperty或selectKey获取主键ID,确保主键为自... 目录 两种方式获取自增 ID：1. ​​useGeneratedKeys+keyProperty（推
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2