去马赛克（Demosaic）二

本文主要是介绍去马赛克（Demosaic）二，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

边缘自适应插值

参考博文图像处理之边缘自适应的插值算法。首先提出从水平和垂直两个方向对绿色分量进行插值重建，先设计由亮度信号的梯度和色度信号的二阶微分构成的边缘检测算子，由边缘检测算子指示沿正确的方向进行绿色分量的插值。红色和蓝色分量的重建使用已经重建好的绿色分量，采用红绿色差空间或蓝色色差空间的线性插值来完成。

在这里插入图片描述

绿色分量重建

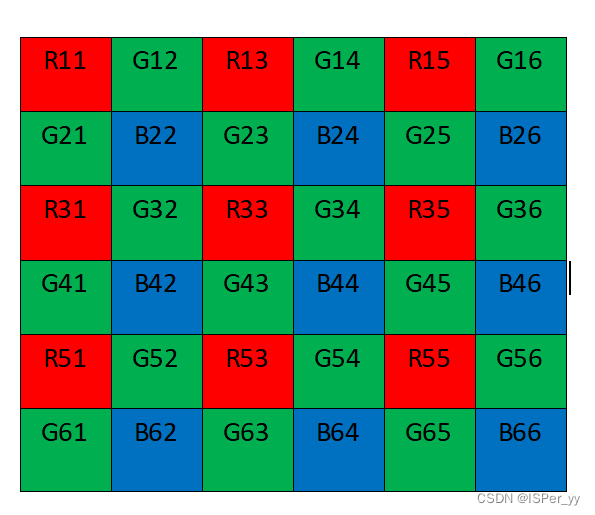
$\quad\quad$ 首先恢复红色和蓝色采样点处的绿色分量，以R33为例，水平方向和垂直方向检测算子计算：

$h = A BS (G 32 - G 34) + A BS (2 R 33 - R 31 - R 35)$
$v = A BS (G 23 - G 43) + A BS (2 R 33 - R 13 - R 53)$

$\quad\quad$ 当水平算子小于垂直算子时，R33存在水平边缘的概率较大，(3,3)处绿色分量的计算沿水平方向进行:
$\frac{G32+G34}{2}+\frac{2R33-R31-R35}{4}$
$\quad\quad$ 当水平算子大于垂直算子时，R33存在垂直边缘的概率较大，(3,3)处绿色分量的计算沿垂直方向进行，公式如下：
$\frac{G23-G43}{2}+\frac{2R33-R13-R53}{4}$
$\quad\quad$ 倘若水平和垂直的算子相等，则(3,3)处的绿色分量的计算为水平和垂直方向的平均值，公式如下：
$G33=\frac{G23+G32+G34+G43}{4}+\frac{4R33-R13-R31-R35-R55}{4}$

绿色采样点处的红色和蓝色分量重建

以G43为例，(4,3)处的RB通道：
$\frac{R33+R53}{2}+\frac{2G43-G23-G63}{2}$
$\frac{B42+B44}{2}+\frac{2G43-G41-G45}{2}$

红色(蓝色)采样点处的蓝色(红色)分量的重建

以R33为例，(3,3)处的蓝色通道：
$D_{45} = ABS(B24-B42)+ABS(2G33-G24-G42)$
$D_{135} = ABS(B22-B44)+ABS(2G33-G22-G44)$
根据梯度的比较结果，选择合适的插值防线，计算如下：

$\left\{\begin{align*} &\frac{B24+B42}{2}+\frac{2G33-G24-G42}{2},当D_{45}<D_{135}\\ &\frac{B22+B44}{2}+\frac{2G33-G22-G44}{2},当D_{45}>D_{135}\\ &\frac{B24+B42+B22+B44}{4}+\frac{4G33-G24-G42-G22-G44}{4},当D_{45}==D_{135} \end{align*} \right\}$

function Output = Debayer_Adaptiveinter(bayer,pattern)[H,W]     = size(bayer);
Output    = zeros(H,W,3);%% 插值G通道
g1        = [-1 1];
g2        = [-1 0 2 0 -1];G1        = conv2(bayer,g1,'same');
G2        = conv2(bayer,g2,'same');
h         = abs(G1)+abs(G2);G1        = conv2(bayer,g1','same');
G2        = conv2(bayer,g2','same');
v         = abs(G1)+abs(G2);Gh        = conv2(bayer,[0 0.5 0 0.5 0], 'same') + conv2(bayer,[-0.25 0 0.5 0 -0.25], 'same');
Gv        = conv2(bayer,[0 0.5 0 0.5 0]', 'same') + conv2(bayer,[-0.25 0 0.5 0 -0.25]', 'same');
h1        = [0 1/4 0; 1/4 0 1/4; 0 1/4 0];
h2        = [0 0 -1 0 0; 0 0 0 0 0; -1 0 4 0 -1; 0 0 0 0 0; 0 0 -1 0 0]/8;
Gmean     = conv2(bayer,h1, 'same') + conv2(bayer,h2, 'same');switch patterncase 'bggr'F(1:2:H, 2:2:W)  = 1;F(2:2:H, 1:2:W)  = 1;case 'rggb'F(1:2:H, 2:2:W)  = 1;F(2:2:H, 1:2:W)  = 1;case 'grbg'F(1:2:H, 1:2:W)  = 1;F(2:2:H, 2:2:W)  = 1;case 'gbrg'F(1:2:H, 1:2:W)  = 1;F(2:2:H, 2:2:W)  = 1;
end
Gp                       = Gh.*(h<v) + Gv.*(h>v) + Gmean.*(h==v);
G                        = bayer.*F+(1-F).*Gp;
% figure;imshow(G,[])%% 插值RB分量
f1           = [0.5 0 0.5];
f2           = [-1 2 -1]/4;
GRBh         = conv2(bayer,f1,"same") + conv2(G,f2,'same');
GRBv         = conv2(bayer,f1',"same") + conv2(G,f2','same');h45          = [0 0 1; 0 0 0; -1 0 0];
h135         = [1 0 0; 0 0 0; 0 0 -1];
Gh45         = [0 0 -1; 0 2 0; -1 0 0];
Gh135        = [-1 0 0; 0 2 0; 0 0 -1];D45          = abs(conv2(bayer,h45,'same'))+abs(conv2(G,Gh45,'same'));
D135         = abs(conv2(bayer,h135,'same'))+abs(conv2(G,Gh135,'same'));RB45         = conv2(bayer,[0 0 0.5; 0 0 0; 0.5 0 0],'same')+conv2(G,[0 0 -0.5; 0 1 0; -0.5 0 0],'same');
RB135        = conv2(bayer,[0.5 0 0; 0 0 0; 0 0 0.5],'same')+conv2(G,[-0.5 0 0; 0 1 0; 0 0 -0.5],'same');
RBmean       = conv2(bayer,[0.25 0 0.25; 0 0 0; 0.25 0 0.25],'same')+conv2(G,[-0.25 0 -0.25; 0 1 0; -0.25 0 -0.25],'same');D            = RB45.*(D45<D135) + RB135.*(D45>D135) + RBmean.*(D45==D135);
switch patterncase 'bggr'R(2:2:H,2:2:W) = bayer(2:2:H,2:2:W);R(1:2:H,2:2:W) = GRBv(1:2:H,2:2:W);R(2:2:H,1:2:W) = GRBh(2:2:H,1:2:W);R(1:2:H,1:2:W) = D(1:2:H,1:2:W);B(1:2:H,1:2:W) = bayer(1:2:H,1:2:W);B(1:2:H,2:2:W) = GRBh(1:2:H,2:2:W);B(2:2:H,1:2:W) = GRBv(2:2:H,1:2:W);B(2:2:H,2:2:W) = D(2:2:H,2:2:W);case 'rggb'R(1:2:H,1:2:W) = bayer(1:2:H,1:2:W);R(1:2:H,2:2:W) = GRBh(1:2:H,2:2:W);R(2:2:H,1:2:W) = GRBv(2:2:H,1:2:W);R(2:2:H,2:2:W) = D(2:2:H,2:2:W);B(2:2:H,2:2:W) = bayer(2:2:H,2:2:W);B(1:2:H,2:2:W) = GRBv(1:2:H,2:2:W);B(2:2:H,1:2:W) = GRBh(2:2:H,1:2:W);B(1:2:H,1:2:W) = D(1:2:H,1:2:W);case 'grbg'R(1:2:H,2:2:W) = bayer(1:2:H,2:2:W);R(1:2:H,1:2:W) = GRBh(1:2:H,1:2:W);R(2:2:H,2:2:W) = GRBv(2:2:H,2:2:W);R(2:2:H,1:2:W) = D(2:2:H,1:2:W);B(2:2:H,1:2:W) = bayer(2:2:H,1:2:W);B(1:2:H,1:2:W) = GRBv(1:2:H,1:2:W);B(2:2:H,2:2:W) = GRBh(2:2:H,2:2:W);B(1:2:H,2:2:W) = D(1:2:H,2:2:W);case 'gbrg'R(2:2:H,1:2:W) = bayer(2:2:H,1:2:W);R(1:2:H,1:2:W) = GRBv(1:2:H,1:2:W);R(2:2:H,2:2:W) = GRBh(2:2:H,2:2:W);R(1:2:H,2:2:W) = D(1:2:H,2:2:W);B(1:2:H,2:2:W) = bayer(1:2:H,2:2:W);B(1:2:H,1:2:W) = GRBh(1:2:H,1:2:W);B(2:2:H,2:2:W) = GRBv(2:2:H,2:2:W);B(2:2:H,1:2:W) = D(2:2:H,1:2:W);            
end
Output = cat(3,R,G,B);
end