本文主要是介绍【博弈论】协调类博弈:纳什均衡的选择,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
这章讨论协调类博弈,也就是有多个NE时,NE的选择的问题。
一、战争博弈
两国可能发生战争,都打的话就打起来了,大家收益各为-5,但是都和平的话收益就都各为10,一个打,一个不打,打了的8,挨打的-10。
这个博弈最终有两个均衡,那就是都打或都不打,但明显都不打是好的结果,这个均衡叫做Pareto NE,就是首先是个均衡,其次是总收益最高的NE。
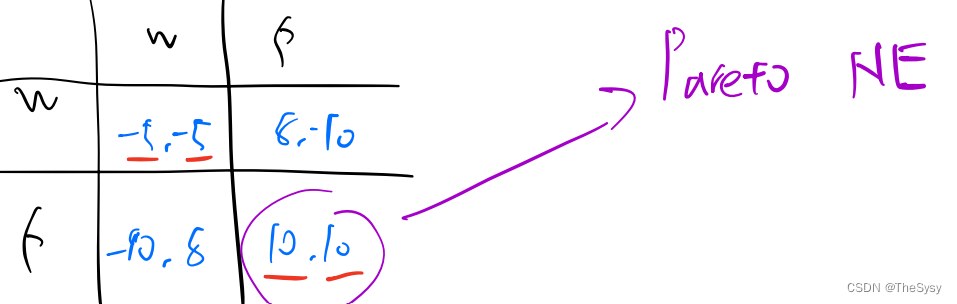
二、打猎博弈
两个人可以选择去狩猎鹿和兔子,但是鹿需要两个人合作才能狩猎。
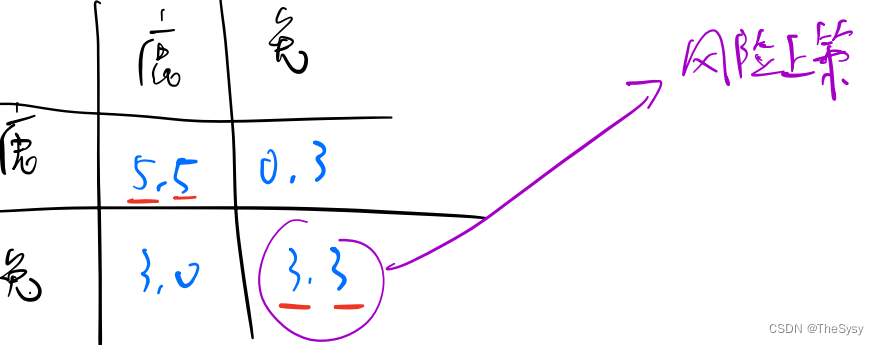
如果两人都选鹿,那就可以吃个大的,5,5。如果只有一个人选鹿,那这个选鹿的就要饿肚子。选兔子一个人就可以,但是只有3的收益。
这个博弈也是有两个均衡,(5,5)就是刚才的Pareto NE,这个(3,3),叫做风险上策。
三、选校小游戏
有7个学校,两个人选,选的一样就有收益,不一样就没有。
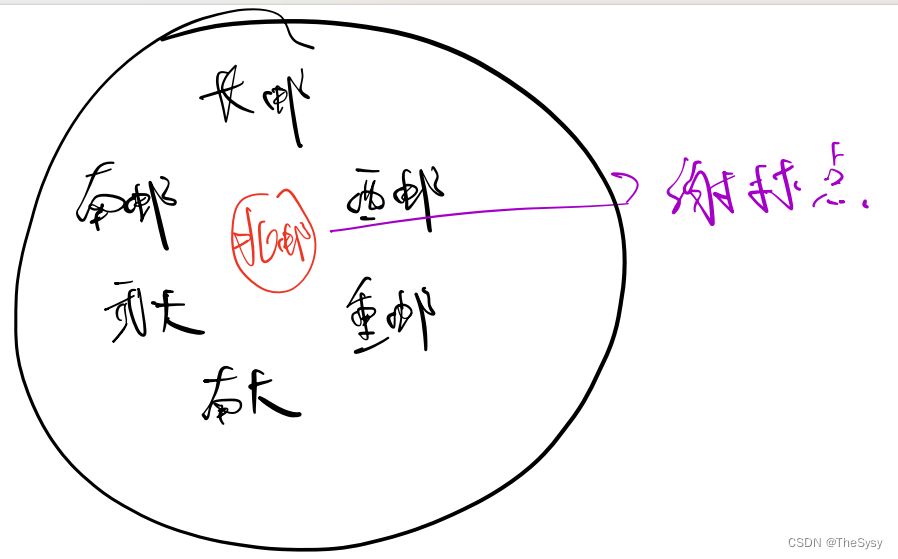
这个博弈有七个NE,就是双方选一样的学校,分别七所学校七种情况。
这个游戏里,有一个很微妙的点,就是如果是在北邮进行,那么大家就会倾向于都选北邮,这样七个NE就趋向了北邮这个NE,这个点叫做谢林点(Schelling point)。
四、赌徒游戏
N个人围一圈,这n个人之外的一个组织者给这n个人分别发钱,每个人都只知道自己收到了多少钱。
之后让大家分别报数,报自己想要的钱的数量,如果大家报的数的和小于等于发出去的钱,那就按报的这个数重新分配钱。如果超过了,那就一分没有。
这个博弈也有很多均衡,只要大家报的数的和等于发出去的和,那就是一个均衡。
这里的谢林点就在所有人都报自己实际获得的钱。
这篇关于【博弈论】协调类博弈:纳什均衡的选择的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






