【Dlib人脸检测】1. HOG特征描述方法

【 1. Harr级联人脸检测、Dlib人脸检测器 】

OpenCV中的Harr级联人脸检测算是人脸识别中早期的检测方法，现在Dlib库在业内开始流行。因为很大程度上是其使用的HOG-SVM人脸检测比OpenCVHarr级联人脸检测效果更好。
当然，现在两个库中也都集成了基于深度学习方法的人脸检测算法。

• OpenCV中Harr级联人脸检测优缺点

优点：
几乎可以在CPU上实时工作；
架构简单；
可以检测不同比例的人脸。

缺点
会出现大量的把非人脸预测为人脸的情况；
不适用于非正面人脸图像；
不抗遮挡。

• Dlib中HOG-SVM人脸检测级优缺点

优点：
CPU上最快的方法；
适用于正面和略微非正面的人脸；
模型很小；
在小的遮挡下仍可工作。

缺点：
不能检测小脸，因为它训练数据的最小人脸尺寸为80×80，但是用户可以用较小尺寸的人脸数据自己训练检测器；
边界框通常排除前额的一部分甚至下巴的一部分；
在严重遮挡下不能很好地工作；
不适用于侧面和极端非正面，如俯视或仰视。

【 2. HOG的定义】

• HOG定义：

方向梯度直方图（Histogram of Oriented Gradient, HOG）是一种在计算机视觉和图像处理中用来进行物体检测的特征描述方法（特征描述方法：就是通过从图像中提取有用信息和丢弃无关信息来简化图像，并将信息运用于算法）。

• HOG提取的图像信息：

1. 特征描述方法从图像中提取有用信息

2. 在图像中，物体的边缘和角落包含了关于物体形状的更多信息，也就是我们平时能看到的物体轮廓。如果能够提取出图像边缘和角落的信息，将非常有利于物体检测。

3. 而对于图像的边缘和角落周围的梯度这个特征，变化幅度很大，所以在HOG特征描述方法中，使用梯度方向的分布（直方图）作为它的特征。

【 3. HOG算法的基本流程 】

• HOG算法的基本流程的基本4步流程：
  ① 计算图像梯度；
  ② 计算Cell中的梯度直方图；
  ③ Block归一化；
  ④ 计算HOG特征。

1. 计算图像梯度

在HOG特征描述方法中，梯度方向的分布（直方图）被用作它的特征。

• 图像梯度是什么 ？

1. 图像是由一个个像素点组成的，可以将图像看成二维离散函数f(x,y)。
2. 图像函数f(x,y)在点(x,y)的梯度G(x,y)是一个具有大小和方向的矢量，设G_x和 G_y分别表示水平 x 方向和垂直 y 方向的梯度.

• 图像梯度公式：
  经典的图像梯度算法是考虑图像的每个像素的某个邻域内的灰度变化。
  图像梯度的计算公式:
  $$G_x(i,j)=I(i+1,j)-I(i,j)$$
  $$G_y(i,j)=I(i,j+1)-I(i,j)$$
  $$G(i,j)=G_x(i,j)+G_y(i,j)$$
  $$\theta (i,j)=arctan\frac{G_x(i,j)}{G_y(i,j)}$$
  其中 I(i,j)表示 (i,j) 像素点处的图像的像素值, θ(i,j)表示 (i,j) 像素点梯度的角度。
• OpenCV计算图像梯度

import cv2
import numpy as np
img = cv2.imread("picture.jpg")
img = np.float32(img) / 255.0#计算图像所有像素点的水平梯度，保存在sobelx中。1，0参数表示在x方向求一阶导数
gx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)#计算图像所有像素点的垂直梯度，保存在sobely中。0,1参数表示在y方向求一阶导数
gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)#进而求得所有图像的梯度以及梯度角度
#其中magnitude表示梯度，angle表示magnitude对应的梯度的角度
magnitude, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)

2. 计算Cell中的梯度直方图

1. 像素梯度分析的拓展： Cell
   由于分析每一个像素的梯度太过细节化了，如果能从更高的角度上观察图像片更能观察出图像的一些规律，而Cell就是在像素的更高的角度。

2. Cell 和 9-bins直方图
   在OpenCV中一个Cell默认是8x8个像素，所以一个Cell中其实包含了8x8 = 64个梯度与梯度角度对，这些对最终都会映射到9-bins直方图，而9-bins直方图就是横坐标有9个点的直方图。

3. 梯度的角度
   首先得说明的是，梯度的角度是介于0和180度之间，而不是0到360度，也就是说某个角度以及它的负数会由相同的数字表示。
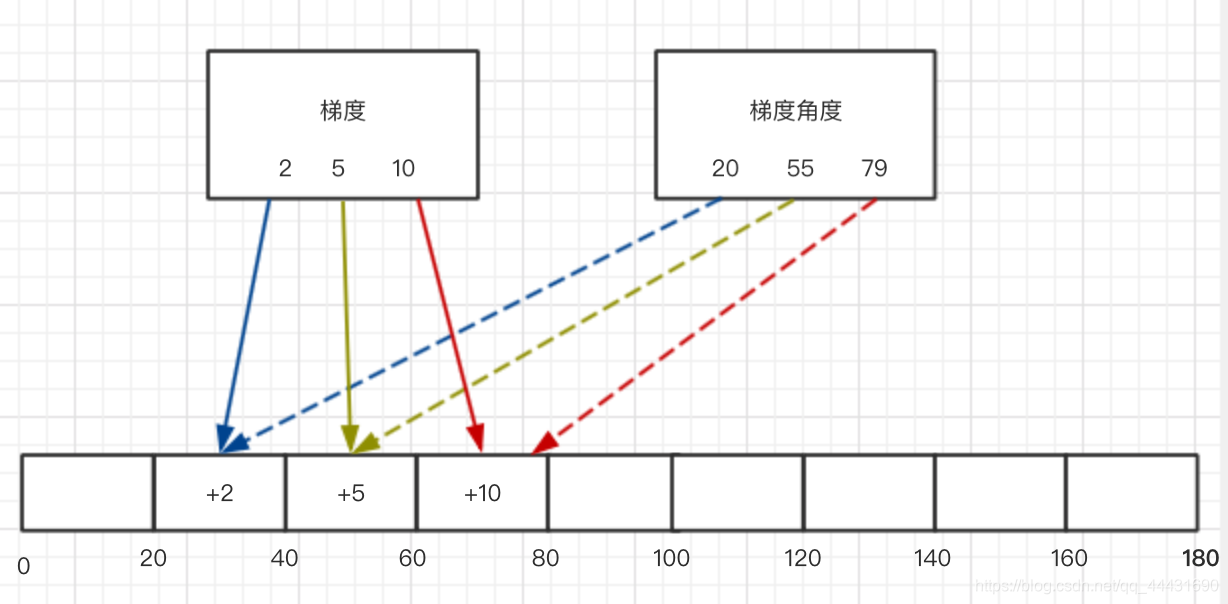
   而在9-bin直方图中，横坐标上的点分别是 0, 20, 40 … 180，这些值就代表梯度的角度。

4. 梯度映射到9-bin直方图
   我们上面说到梯度与梯度角度对最终都会映射到直方图中，那如何映射呢？举个简单的例子吧，现在有一个(5,55)对，即其梯度为5、梯度角度为55度，它位于[40度,60度]之间，那么它会映射到第3个bins，第3个bins的值会加上他的梯度，也就是加上5。
   如下图:
   
   也就是说，梯度角度决定了映射的bins，梯度决定了映射的值。这样我们就可以求出每个cell的梯度直方图了。

3. Block 归一化

• 目的：
  梯度对于图像的光照亮度是十分敏感的，一般需要对梯度做归一化处理以消除亮度变化的影响。

• 方法：
  在HOG采取的方法是：把 Cell 组合成大的、空间上连通的区块（Blocks）。
  在OpenCV中，默认Block的大小为16x16个像素点，也就是2x2个Cell。
  如下图：
  

• 归一化的理解：

1. 假设有一个向量v1，它的值为[128,64,32]。经过计算可得，该向量长度是:$\sqrt{128^2+64^2+32^2}=146.64$
   将该向量的每个元素除以146.64，得到归一化向量[0.87,0.43,0.22]。
   .
2. 同样的，如果将v1 x 2，能得到新向量v2[256,1268,64]，对其归一化的结果仍然为[087,0.43,0.22]，也就是说归一化会去除数值大小的影响。
   .
3. 如果我们对Block归一化处理，当光照强度变化大时，该区域的梯度值普遍会更大，从而减少了光照的影响。
   .
4. 虽然我们可以以Cell为单位，对图片进行归一化处理，但更好的是在比Cell更大尺寸的Block上进行归一化。因为Block的像素点更多，受到光照的影响会更小。在一个16×16块中有将包含4个Cell，那么一个块中就可以连接形成一个长度为4x9=36的向量(1个Cell中包含9个Bins)。

4. 计算HOG特征

将所有的block归一化后得到的向量合起来就形成了一个HOG特征。

• 为了计算一张图片的所有HOG特征，需要计算所有的Block。通过移动Block窗口的方式进行一 一计算，其过程如下图所示：
  

【 4. 使用OpenCV计算HOG特征 】

上面我们详细的讲解了Hog特征描述方法的原理。现在我们可以借助OpenCV中封装好的方法来计算HOG特征。

1. 首先，使用cv2.HOGDescriptor()函数声明HOG特征描述方法，代码如下：

hog = cv2.HOGDescriptor() #使用cv2.HOGDescriptor()函数声明HOG特征描述方法

2. 然后计算加载的图像的HOG特征值，代码如下：

h = hog.compute(img) #计算加载的图像的HOG特征值

• 完整的代码示例如下：

import cv2hog = cv2.HOGDescriptor()#使用cv2.HOGDescriptor()函数声明HOG特征描述方法img = cv2.imread("picture.jpg")# 读取图片feature = hog.compute(img)
print(feature)