SDOI2009HH的项链

本文主要是介绍SDOI2009HH的项链，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

HH有一串由各种漂亮的贝壳组成的项链。HH相信不同的贝壳会带来好运，所以每次散步
完后，他都会随意取出一段贝壳，思考它们所表达的含义。HH不断地收集新的贝壳，因此，
他的项链变得越来越长。有一天，他突然提出了一个问题：某一段贝壳中，包含了多少种不同
的贝壳？这个问题很难回答。。。因为项链实在是太长了。于是，他只好求助睿智的你，来解

决这个问题。

在线貌似不可做？

可以用离线算法，先预处理出与当前位置颜色相同的下一个颜色在哪，然后对每一个询问按左端点排序，对于每一个询问，将其查询区间左边的所有“下一个颜色“位置的值加1，

答案即为（右端点）前缀和减去（左端点减一）前缀和之差。

答案正确性证明：

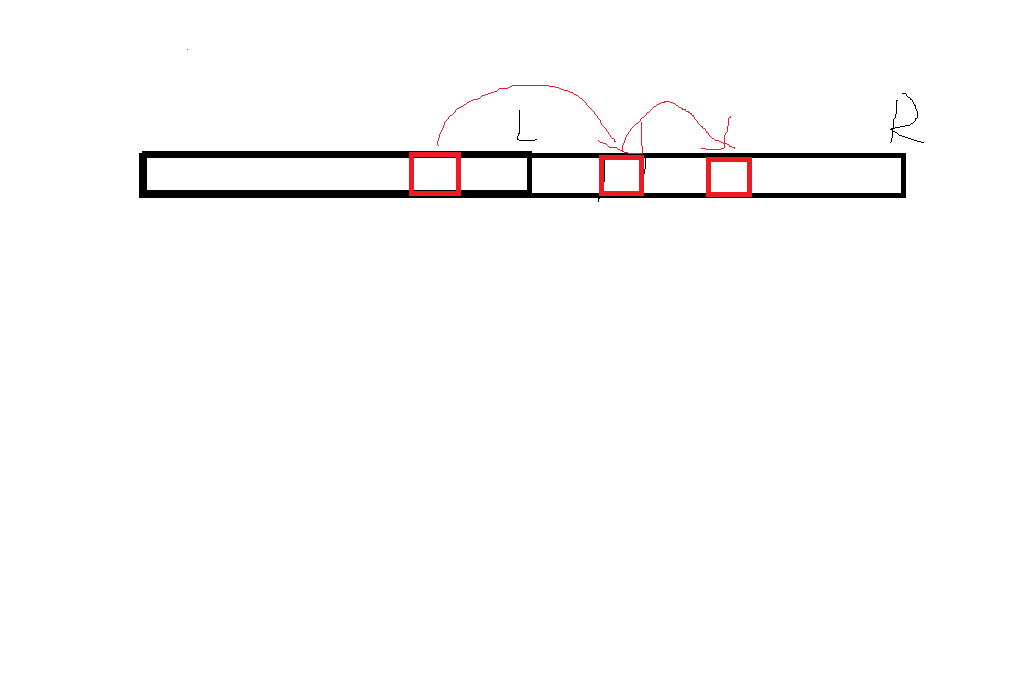
因为要相减，所以1-（左端点-1）不用考虑，因为相减抵消了，而在当前区间内，没出现过的不用讨论，而出现过的因为只计算其区间左端点之前的“下一个颜色位置”，所以不会计算多次，如下：

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn=50000+10;
int a[maxn];
int next[1000010]={0};
int p[1000010]={0};
int s[maxn];
int n,m;
struct T{
    int l,r,id;
    bool operator<(const T&c)const{
        if(l==c.l)
            return r<c.r;
        return l<c.l;
    }
}A[200010];
int ans[200010];
inline void add(int x,int p){
    while(x<=n){
        s[x]+=p;
        x+=x&(-x);
    }
}
inline int sum(int x){
    int tmp=0;
    while(x){
        tmp+=s[x];
        x-=x&(-x);
    }
    return tmp;
}
int main(){
    freopen("diff.in","r",stdin);
    freopen("diff.out","w",stdout);
    int mx=0;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]),mx=max(mx,a[i]);
    for(int i=n;i>=1;i--)
        next[i]=p[a[i]],p[a[i]]=i;
    for(int i=0;i<=mx;i++)
        if(p[i])
            add(p[i],1);
    scanf("%d",&m);
    for(int i=1;i<=m;i++)
        scanf("%d %d",&A[i].l,&A[i].r),A[i].id=i;
    sort(A+1,A+m+1);
    int l=1;
    for(int i=1;i<=m;i++){
        while(l<A[i].l){
            if(next[l])
                add(next[l],1);
            l++;
        }
        ans[A[i].id]=sum(A[i].r)-sum(A[i].l-1);
    }
    for(int i=1;i<=m;i++)
        printf("%d\n",ans[i]);
return 0;
}

这篇关于SDOI2009HH的项链的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---