【一百一十】【算法分析与设计】[SDOI2009] HH的项链,树状数组应用,查询区间的种类数,树状数组查询区间种类数

本文主要是介绍【一百一十】【算法分析与设计】[SDOI2009] HH的项链,树状数组应用,查询区间的种类数,树状数组查询区间种类数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

P1972 [SDOI2009] HH的项链

[SDOI2009] HH的项链

题目描述

HH 有一串由各种漂亮的贝壳组成的项链。HH 相信不同的贝壳会带来好运，所以每次散步完后，他都会随意取出一段贝壳，思考它们所表达的含义。HH
不断地收集新的贝壳，因此，他的项链变得越来越长。

有一天，他突然提出了一个问题：某一段贝壳中，包含了多少种不同的贝壳？这个问题很难回答……
因为项链实在是太长了。于是，他只好求助睿智的你，来解决这个问题。

输入格式

一行一个正整数 $n$，表示项链长度。 第二行 $n$ 个正整数 $a_i$，表示项链中第 $i$ 个贝壳的种类。

第三行一个整数 $m$，表示 HH 询问的个数。 接下来 $m$ 行，每行两个整数 $l,r$，表示询问的区间。

输出格式

输出 $m$ 行，每行一个整数，依次表示询问对应的答案。

样例 #1

样例输入 #1

6 1 2 3 4 3 5 3 1 2 3 5 2 6

样例输出 #1

2 2 4

提示

【数据范围】

对于 $20\%$ 的数据，$1\le n,m\le 5000$； 对于 $40\%$ 的数据，$1\le n,m\le 10^5$； 对于 $60\%$ 的数据，$1\le n,m\le 5\times 10^5$； 对于 $100\%$
的数据，$1\le n,m,a_i\le 10^6$，$1\le l\le r\le n$。

本题可能需要较快的读入方式，最大数据点读入数据约 20MB

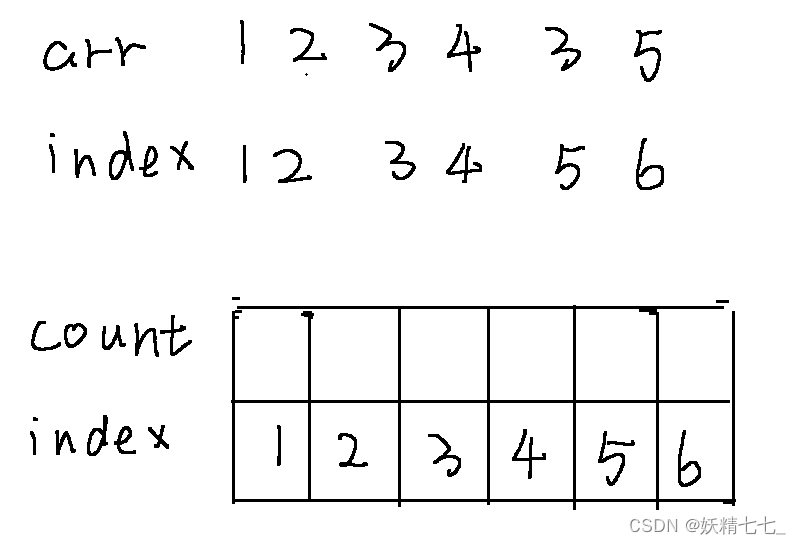
用count数组记录每一个位置种类数,实际上每一个位置都算作是1.
如果每一个位置都是1.

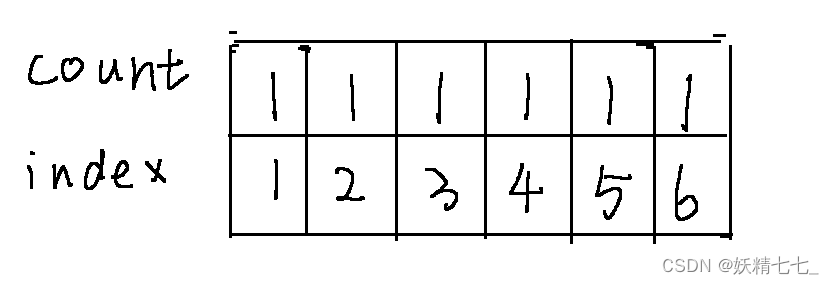
计算1~ 4区间的种类数是1~ 4区间count数组的累加和结果.
因为1~ 4区间中的种类数全部都没有出现重复的情况.
但是如果要计算3~ 5区间的种类数是多少,那么就需要对3和5哪一个位置进行去重的处理.

如果我们查询的区间是l~ r.

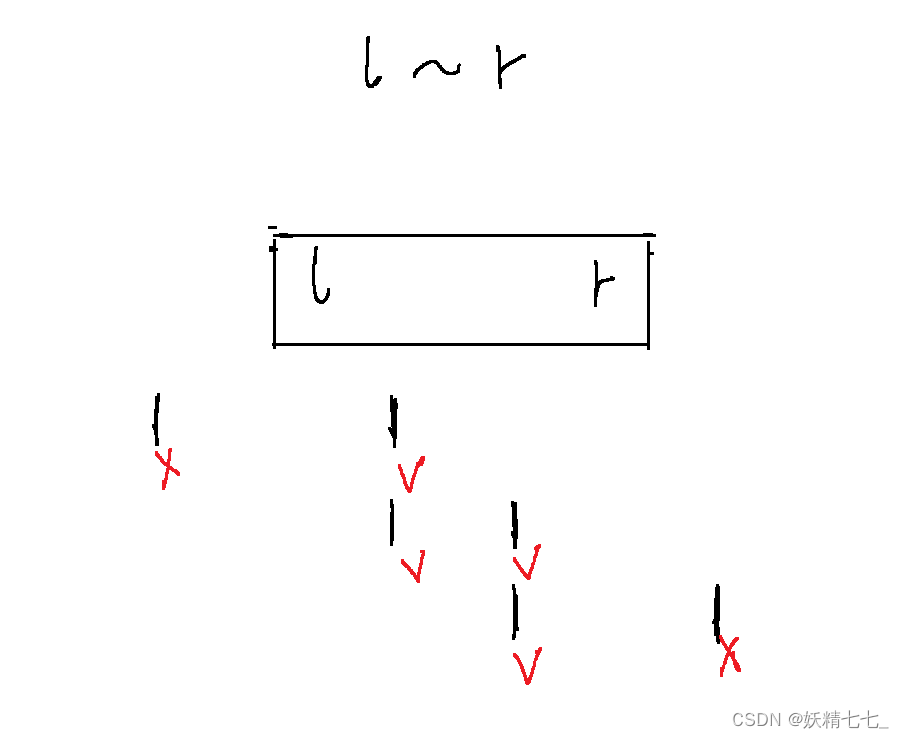
1表示重复的种类的1出现的位置,那么打叉的地方是需要进行去重的,打勾的地方是可以选择保留的地方.
针对于第三种情况,r右边出现的1我们并不关心,因为一定不在查询区间中.
因此可以按照查询的右区间从小到大排序,只维护r左边count值即可.
现在我们就只需要维护好r左边的count值就可以了.
也就是第一种情况和第二种情况,第二种情况因为都在区间内,所以不管去掉哪一个都可以,但是第一种情况只能去掉左边的.
因此我们可以按照这样的规则,只保留最右边的1.因为如果包含最右边的1,其他的可以被代替,如果没有包含最右边的1,其他的1也没有意义.
所以只需要关心最右边的1即可.

按照查询的右区间进行排序,然后只维护r左边的count值.
当前位置是i=1位置,然后维护1~ r区间的count值,每一次都添加1,但是每一次遍历i位置的时候需要考虑是否需要去重操作.
也就是需要查询arr[i]元素最右侧的1是否出现,如果出现了就需要先减少1.

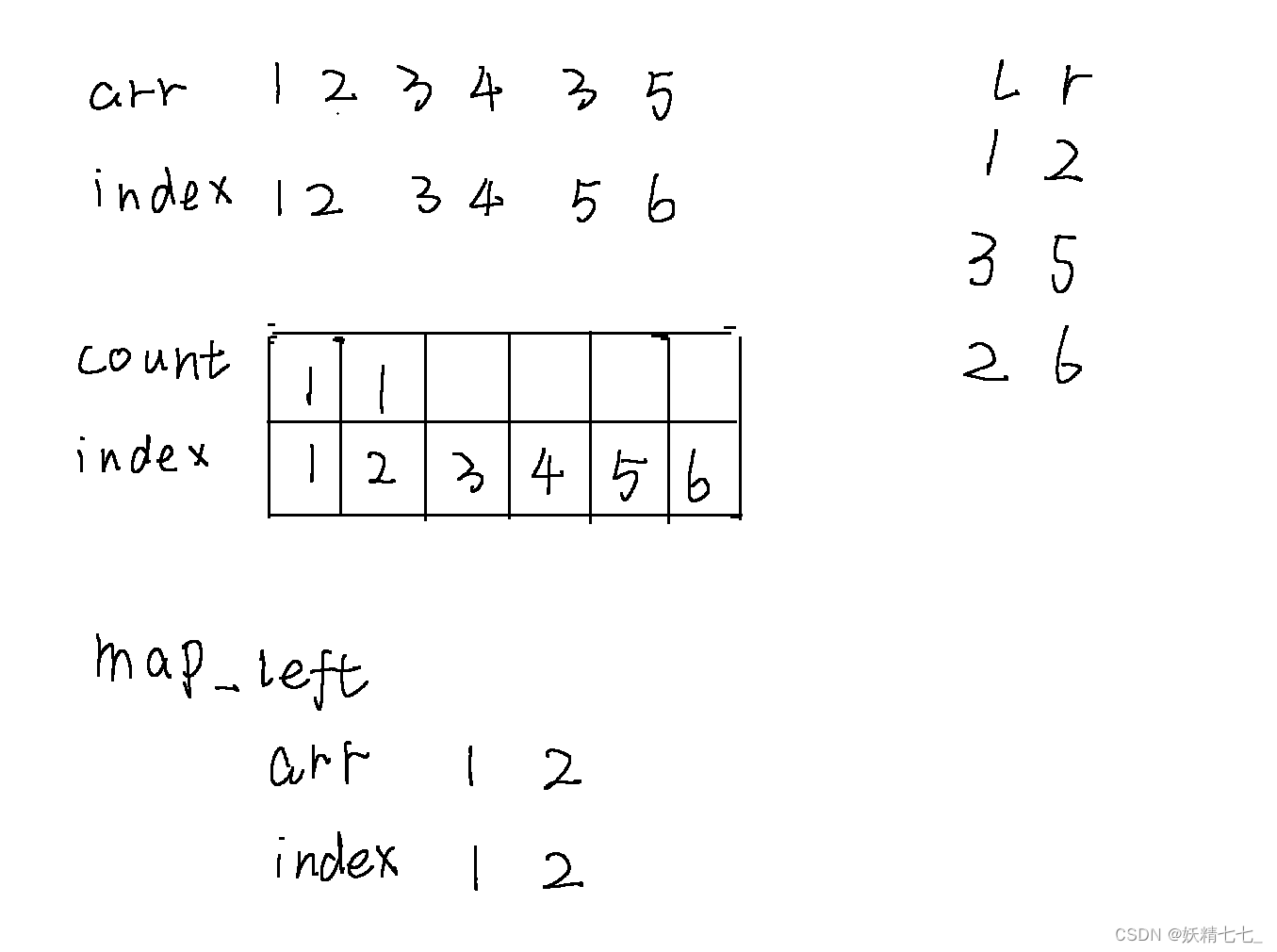
第一次查询结果是count数组1~ 2累加和,答案是2

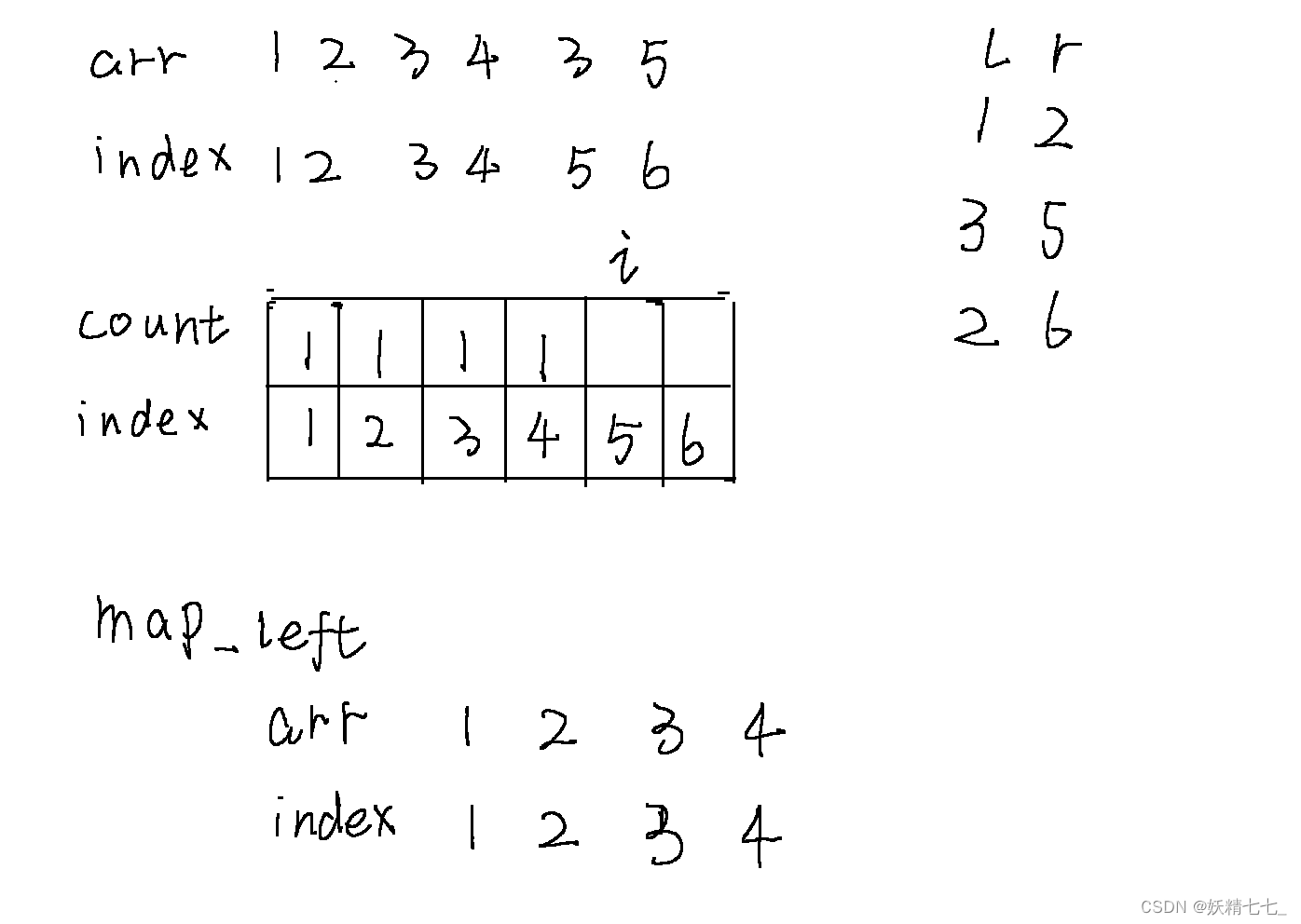
当i遍历到5的时候,我们查询map_left发现5位置的元素3之前出现过,位置是3,所以需要进行去重操作,将3位置count值减少1,然后5位置count值增加1.并且将维护arr_left值,元素3最右边的下标是5.

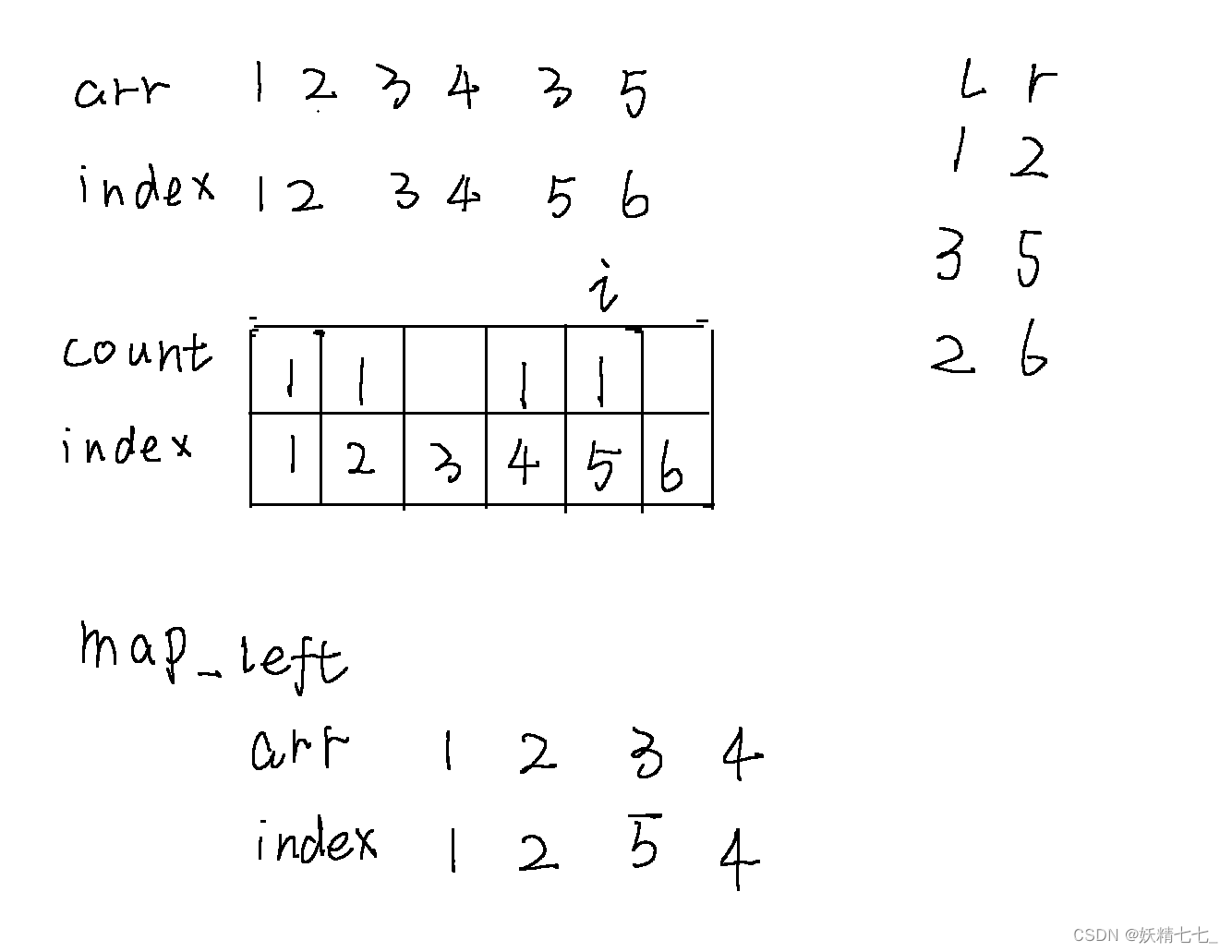
此时查询3~ 5区间的种类数是count3~ 5区间累加和,答案是2.

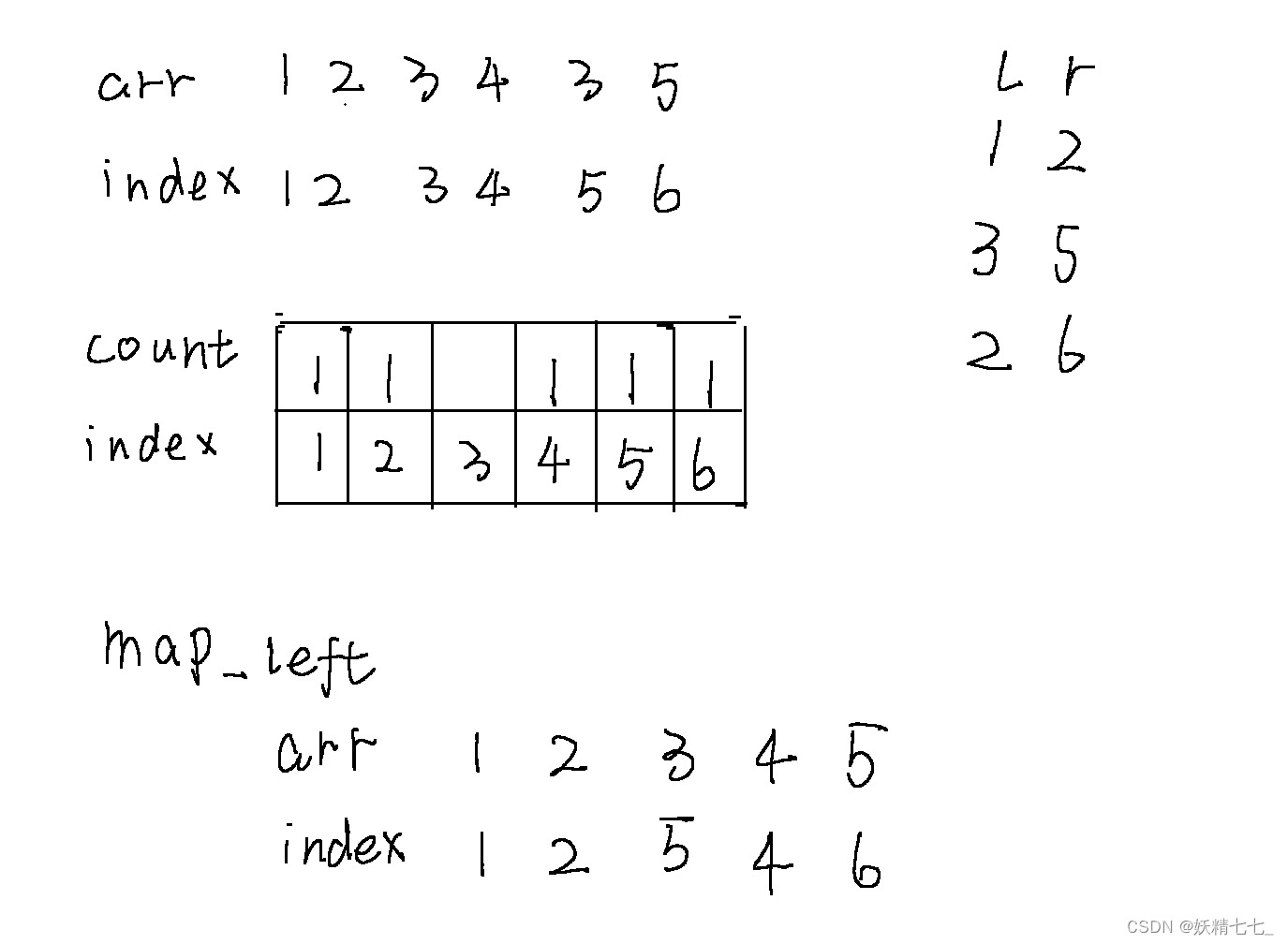
查询2~ 6区间的种类数,也就是count2~ 6区间累加和,答案是4.

#include<bits/stdc++.h>
using namespace std;#define int long long // 将 int 定义为 long long 类型
#define endl '\n' // 将 endl 定义为换行符int n; // 定义整数 n，表示数组长度
vector<int>arr; // 定义一个整型向量 arr，用于存储数组元素
int q; // 定义整数 q，表示查询次数
struct node {int l, r, index; // 定义结构体 node，包含三个整型变量 l, r 和 index
};
vector<node>readd; // 定义一个 node 类型的向量 readd，用于存储查询
map<int, int>arr_left; // 定义一个映射 arr_left，用于记录元素上次出现的位置
class Tree {
public:vector<int>tree; // 定义一个整型向量 tree，用于树状数组int lowbit(int i) { // 返回 i 的最低位 1 的值return i & -i;}void sett(int i, int v) { // 在树状数组中更新值while (i < tree.size()) {tree[i] += v;i += lowbit(i);}}int gett(int i) { // 获取前 i 项的和int ret = 0;while (i > 0) {ret += tree[i];i -= lowbit(i);}return ret;}int range(int l, int r) { // 获取区间 [l, r] 的和return gett(r) - gett(l - 1);}
};
Tree t1; // 定义一个 Tree 类的对象 t1
void init() { // 初始化函数cin >> n; // 输入数组长度arr.assign(n + 1, 0); // 将数组大小设为 n+1，并初始化为 0for (int i = 1; i <= n; i++) {cin >> arr[i]; // 输入数组元素}readd.clear(); // 清空 readd 向量cin >> q; // 输入查询次数for (int i = 1; i <= q; i++) {int l, r;cin >> l >> r; // 输入每个查询的左右边界readd.push_back({ l,r,i }); // 将查询添加到 readd 向量中}
}
vector<int>ret; // 定义整型向量 ret，用于存储结果
void solve() {sort(readd.begin(), readd.end(), [](const node& a, const node& b) { // 按照查询的右边界 r 进行排序return a.r < b.r;});ret.assign(q + 1, -1); // 将 ret 大小设为 q+1，并初始化为 -1t1.tree.assign(arr.size() + 1, 0); // 初始化树状数组arr_left.clear(); // 清空 arr_left 映射int i = 1;for (auto& xx : readd) {int l = xx.l, r = xx.r, index = xx.index; // 取出每个查询的 l, r 和 indexwhile (i <= r) {if (arr_left.count(arr[i])) { // 如果元素已在 arr_left 中记录过int index1 = arr_left[arr[i]]; // 取出上次出现的位置t1.sett(index1, -1); // 在树状数组中将该位置的值减 1}arr_left[arr[i]] = i; // 更新 arr_left 中该元素的最新位置t1.sett(i, 1); // 在树状数组中将当前元素位置的值加 1i++;}ret[index] = t1.range(l, r); // 计算区间 [l, r] 的和并存储在 ret 中}for (int i = 1; i < ret.size(); i++) {cout << ret[i] << endl; // 输出每个查询的结果}}signed main() {ios::sync_with_stdio(0), cin.tie(), cout.tie(0); // 加速输入输出init(); // 调用初始化函数solve(); // 调用解决函数
}

结尾

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。
同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。
谢谢您的支持，期待与您在下一篇文章中再次相遇！

这篇关于【一百一十】【算法分析与设计】[SDOI2009] HH的项链,树状数组应用,查询区间的种类数,树状数组查询区间种类数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---