本文主要是介绍图神经网络DGL-构图,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
图神经网络DGL-构图
图神经网络、图表示学习、知识图谱
GNN的学习目标是获得每个结点的图感知的隐藏状态,这就意味着:对于每个节点,它的隐藏状态包含了来自邻居节点的信息。
TF-IDF算法介绍及实现
图神经网络—基本概念与手写code
【图计算】 DGL-构图与用图
DGL-图属性
dgl.DGLGraph是对图的统一抽象,它存储了图的结构信息、节点/边的属性信息。
- 通过dgl.graph()生成同构图
- 通过dgl.heterograph()生成异构图
- 借助dgl.*工具包和其他数据源生成图
备注:在DGL眼中图都是有向的。对于无向图,用户需要为每条边创建两个方向的边,具体需调用dgl.to_bidirected()方法。
实现GCN 需要具备message信息 和 reduce信息
一、同构图
同构图:图中只有一种类型的节点、一种类型的边。
import networkx as nx
import dgl
import torch
import numpy as np
#import scipy.sparse as sppu = torch.tensor([0, 0, 0, 0, 0])
v = torch.tensor([1, 2, 3, 4, 5])
G = dgl.graph((u, v))
print(G)
# Graph(num_nodes=6, num_edges=5,
# ndata_schemes={}
# edata_schemes={})
#获取节点的ID
print(G.nodes())
# tensor([0, 1, 2, 3, 4, 5])
#获取边对应端点
print(G.edges())
# (tensor([0, 0, 0, 0, 0]), tensor([1, 2, 3, 4, 5]))
#获取边对应的端点和边ID
print(G.edges(form = 'all'))
# (tensor([0, 0, 0, 0, 0]), tensor([1, 2, 3, 4, 5]), tensor([0, 1, 2, 3, 4]))
#用户可以在构建图的时候,指明节点的数量
G = dgl.graph((u, v), num_nodes = 8)
print(G)
# Graph(num_nodes=8, num_edges=5,
# ndata_schemes={}
# edata_schemes={})访问节点、边的属性信息:通过graph.ndata访问节点属性,通过graph.edata访问边属性
import networkx as nx
import dgl
import torch
import numpy as np
#import scipy.sparse as sppu = torch.tensor([0, 0, 1, 5])
v = torch.tensor([1, 2, 2, 0])
G = dgl.graph((u, v)) #6个节点, 4条边
print(G)
# Graph(num_nodes=6, num_edges=4,
# ndata_schemes={}
# edata_schemes={})
G.ndata['x'] = torch.ones(G.num_nodes(), 3) #长度为3的节点特征, 矩阵大小为(6, 3)
G.edata['x'] = torch.ones(G.num_edges(), dtype = torch.int32) #边的属性为标量整型特征
print(G)
# Graph(num_nodes=6, num_edges=4,
# ndata_schemes={'x': Scheme(shape=(3,), dtype=torch.float32)}
# edata_schemes={'x': Scheme(shape=(), dtype=torch.int32)})
G.ndata['y'] = torch.randn(G.num_nodes(), 5) #节点y的特征, 节点目前有x和y两种特征
print(G.ndata['x'][1])
# tensor([1., 1., 1.])
print(G.edata['x'][torch.tensor([0, 3])])
# tensor([1, 1], dtype=torch.int32)
print(G)
# Graph(num_nodes=6, num_edges=4,
# ndata_schemes={'x': Scheme(shape=(3,), dtype=torch.float32), 'y': Scheme(shape=(5,), dtype=torch.float32)}
# edata_schemes={'x': Scheme(shape=(), dtype=torch.int32)}) 创建图的过程,还可以通过dgl.to_bidirected直接由单向图创建双向图。
如果在图中有没有边链接的点,需要通过graph函数的num_nodes属性指定有多少单点。
对于有权图,可将权值作为图的边特征存储
# edges 0->1, 0->2, 0->3, 1->3
edges = th.tensor([0, 0, 0, 1]), th.tensor([1, 2, 3, 3])
weights = th.tensor([0.1, 0.6, 0.9, 0.7]) # weight of each edge
g = dgl.graph(edges)
g.edata['w'] = weights
print(g)
# Graph(num_nodes=4, num_edges=4,
# ndata_schemes={}
# edata_schemes={'w' : Scheme(shape=(,), dtype=torch.float32)})
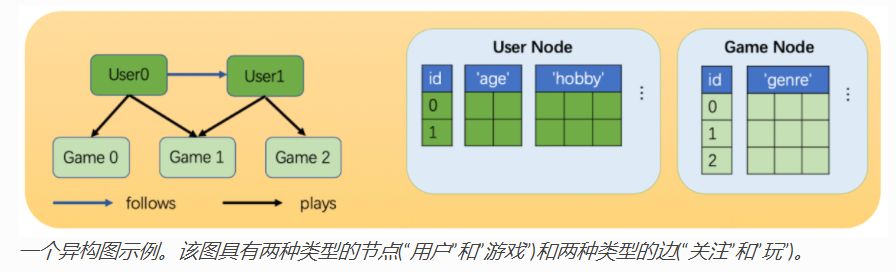
二、异构图
在DGL中,一个异构图由一系列子图构成,一个子图对应一种关系。每个关系由一个字符串三元组定义(源节点类型,边类型,目标节点类型)。
import networkx as nx
import dgl
import torch
import numpy as np#创建具有3个节点类型 和 3种边类型的异构图
graph_data = {('drug', 'interacts', 'drug'):(torch.tensor([0, 1]), torch.tensor([1, 2])), #两条边, drug0 - drug1, drug1 - drug2('drug', 'interacts', 'gene'):(torch.tensor([0, 1]), torch.tensor([2, 3])),('drug', 'treats', 'disease'):(torch.tensor([1]), torch.tensor([2]))
}G = dgl.heterograph(graph_data)print("ntypes = ", G.ntypes)
# ntypes = ['disease', 'drug', 'gene']
print("etypes = ", G.etypes)
# etypes = ['interacts', 'interacts', 'treats']
print("canonical_etypes = ", G.canonical_etypes)
# canonical_etypes = [('drug', 'interacts', 'drug'), ('drug', 'interacts', 'gene'), ('drug', 'treats', 'disease')]
print(G)
# Graph(num_nodes={'disease': 3, 'drug': 3, 'gene': 4},
# num_edges={('drug', 'interacts', 'drug'): 2, ('drug', 'interacts', 'gene'): 2, ('drug', 'treats', 'disease'): 1},
# metagraph=[('drug', 'drug', 'interacts'), ('drug', 'gene', 'interacts'), ('drug', 'disease', 'treats')])
print(G.nodes('drug'))
print(G.nodes('gene'))
print(G.nodes('disease'))
# tensor([0, 1, 2])
# tensor([0, 1, 2, 3])
# tensor([0, 1, 2])
G.nodes['drug'].data['hv'] = torch.ones(3, 1)
G.nodes['drug'].data['k'] = torch.randn(3, 4)
print(G.nodes['drug'].data['hv'])
# tensor([[1.],
# [1.],
# [1.]])
G.edges['treats'].data['he'] = torch.zeros(1, 1)
print(G.edges['treats'].data['he'])
# tensor([[0.]])
print(G.nodes('drug'))
print(G.nodes['drug'])
# tensor([0, 1, 2])
# NodeSpace(data={'hv': tensor([[1.],
# [1.],
# [1.]]),
# 'k': tensor([[ 0.3068, -1.1727, 0.3256, 1.6496],
# [ 2.1131, 1.9972, -0.9089, 1.5092],
# [-0.9954, 2.1767, 0.3712, -0.0139]])})Scipy sparse matrix 作为图的邻接矩阵 转换成dgl的图 : g = dgl.from_scipy(sp.g)
Networkx graph : g = dgl.from_networkx(nx.g)
外部资源创建图
import dgl
import scipy.sparse as spsp_g = sp.rand(100, 100, density=0.5) # 5% nonzero entries
g = dgl.from_scipy(sp_g)
print(g)
# Graph(num_nodes=100, num_edges=5000,
# ndata_schemes={}
# edata_schemes={})import networkx as nx
nxg = nx.path_graph(5) # a chain 0-1-2-3-4
# nx.path_graph constructs an undirected NetworkX graph
g = dgl.from_networkx(nxg)
print(g)
# Graph(num_nodes=5, num_edges=8,
# ndata_schemes={}
# edata_schemes={})nxg = nx.DiGraph([(2, 1), (1, 2), (2, 3), (0, 0)])
# constructs an directed NetworkX graph
g = dgl.from_networkx(nxg)
print(g)
# Graph(num_nodes=4, num_edges=4,
# ndata_schemes={}
# edata_schemes={})
三、二分图
这篇关于图神经网络DGL-构图的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









