Lazy Theta * : 任意角度路径规划及3D空间下的路径分析

原文地址：http://idm-lab.org/bib/abstracts/papers/aaai10b.pdf

1.简介

路径规划是与机器人技术和视频游戏紧密相关的技术，它通常由两个核心问题构成：

• 抽象图数据：将连续地形信息离散化为图数据
• 路线生成：从一个给定的起始点，沿图数据的边进行信息传递和扩展，最终到达给定的目标点

开发者们发明了多种不同的方法来解决抽象图数据的问题，例如2D空间下的基于不同形状（正方形、六边形）的网格，3D空间下的基于不同多边形的网格，可视图，路点图等等。

而另一方便，在解决路线生成问题方面，开发者们通常都会选择A * 算法，因为A * 既高效，又简单，并且能够找到基于网格边缘的最短路径。A * 及传统的寻路算法（这里主要指A * 的各种优化算法）是以网格的边传播和扩展，并且生成的路线也被约束在网格边上。但是基于网格边缘的最短路径并不一定是实际情况下的最短路径（如下图）。

图 1：

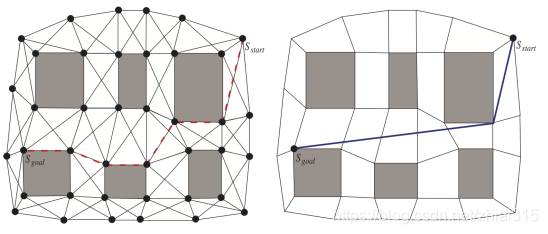
上图表示将一个连续地形离散化为NavMesh，其中的多边形通过黑白表示是否阻隔。左侧图片显示的是通过A * 找到的基于格子边缘的最短路径，右侧图片表示的是实际最短路径。可见，A * 找到的路径比实际最短路径要长更多。

实际上，在2D空间下，基于方格边缘的路线比真实最短路线长出约8%的距离，而在3D空间中，基于立方体边缘的路线比实际最短路线长出的距离增加到了13%左右。因此，Theta * 算法作为一种不依附格子边缘的、可任意角度转向、平滑的寻路算法，可以很好地解决这个问题。然而，在3D空间中邻接点的数量远远大于2D空间中邻接点数量。例如以正方形组成的2D网格中，相邻只有8个邻居，而在以立方体组成的3D网格中，邻居的数量会激增至26个。邻接点数量的增加大大降低了Theta * 算法在3D空间下的效率，因为Theta * 在每次扩展新顶点的时候，都会进行大量的LOS计算。于是，我们提出 Lazy Theta * 算法，通过延迟执行LOS检查，降低LOS的次数，从而提升Theta * 的效率。

2.标记与定义

本文中，我们考虑以立方体单元组成的3D网格。所有立方体单元的顶点的集合记做 V。点S_start表示寻路的起始点，它是某个立方体单元的某个顶点，即 S_start∈V。点S_goal表示寻路的目标点，它也是某个立方体单元的某个顶点，即 S_goal∈V。 L(s, s’)表示从s点到s’点之间的线段。c(s, s’)表示L(s, s’)的长度，也即两点间距离。lineofsight(s, s’)是检查s和s’间是否存在视线（LOS）的方法，当且仅当L(s, s’)不从任何阻隔的立方体单元内部穿过，也不从两个阻隔的立方体单元的共面穿过时，我们认为这两点间是存在LOS的。这里为了简单起见，认为从两个阻隔立方体相交的顶点或者相交的边穿过是允许的。

3. A * 算法

A * 伪代码如下：

图 2：

本文所有讨论都是基于上图 A * 伪代码，并以此为基础进行更改。

在A * 算法中，每个顶点持有两个重要的数据：

• G值：表示从寻路起始点S_start到该点的当前最短距离。
• parent（s）：表示点s的父节点，用于在寻路结束后剥离最终路线。

另外，A * 中还持有两个重要的全局列表：

• open list ： 表示即将扩展的点的优先队列
• close list ： 表示所有已扩展过的点的集合

从上图伪代码中的ComputeCost方法可以看到，对于当前点s的邻接点s’，A * 将起始点s_start到s’的最终路径拆分成s_start → s 和 s → s’ 两部分来考虑，通过这两部分的距离得到总的距离，如果这个g值比当前s’已知的g值（从别的点到达s’点产生的g值）小，则更新g值，并将s’的父节点设置为s。

4. 路径长度分析

原文在本节中定义了最短顶点路径，实际也可理解为就是基于LOS的最短路径，它是与最短边缘路径相对的，最短边缘路径即A * 找出的基于网格边的最短路径。由这三者得到如下关系：
最短边缘路径 ≥ 最短顶点路径 ≥ 最短实际路径

另外，本节中还提出了一些推理和证明，恕在下看不懂。有兴趣的可以去看原文。

5. A * PS

在之前的文章中已经讨论过A * PS，即对A * 的最终路径进行平滑后处理的优化方案，并指出，A * PS 虽然能够平滑路线以及缩短路径，但并不能解决A * 路径与真实最短路径差距较大的问题。这里需要说明的是，在3D空间中，这个问题是依然存在的（如下图）。

图 3：

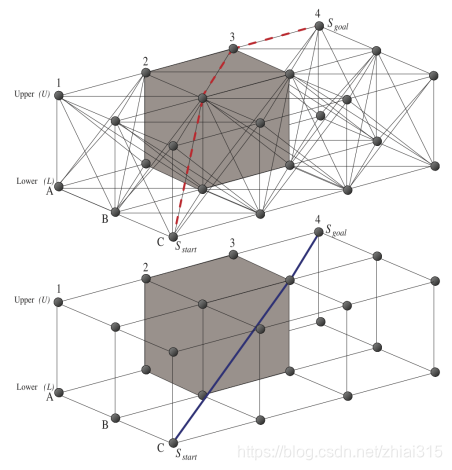
上图中，A * 找到的最短路径是上方图片的红色虚线路径，经过A * PS处理后，会将路径中的点A_3U删除掉，使路径从点B_2U直接连接到目标点S_goal（A_4U）。这条路径相比A * 找到的原始路径更加平滑，且的确距离更短，但是从图中可以看出，处理后的路径依然要比真实最短路径（图中蓝色实线路径）更长。

6. Theta *

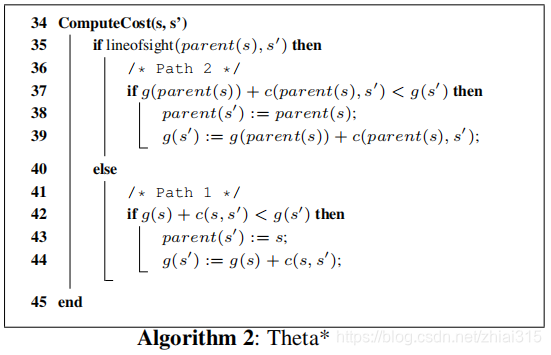
Theta * 是一种不限制角度的寻路方法，它可以在于A * 和 A * PS 近乎相同的时间内找到一条更平滑、距离更短的路径。Theta * 与 A * 关键的区别在于，Theta * 中允许一个顶点的父节点是另外任意一个顶点，而在A * 中，顶点的父节点只能是它的可见邻接点。

对于一个即将扩展的新点s’，Theta * 会考虑两种到达该点的路径方案：

• 路径1：和A * 一样，将s_start到s’的路径拆分成 s_start → s 和 s → s’
• 路径2：将s_start到s’的路径拆分成 s_start→ parent(s) 和 parent(s) → s’

在parent(s) 和 s’ 之间存在LOS的情况下，Theta * 会优先选择路径2，因为根据三角形不等式，两边和大于第三边，路径2一定比路径1更优。下图伪代码展示了Theta * 在选择路径上与A * 的不同之处。

图 4：

7. Lazy Theta *

在本文一开始我们就提到了路径规划的两个核心问题，其中第一个便是抽象图数据问题。理论上讲，能够与多种抽象图数据结构兼容的路线生成算法，其应用的广泛性也会更高。在这一点上，Theta * 并不依赖特定的抽象图数据，它既可以应用在正方形网格上，也可以应用在NavMesh等其他结构上。这得益于它的基础——三角形不等式。

Theta * 最大的问题在于LOS检查带来的消耗。当然，一些现有的画线算法可以在一定程度上降低LOS的复杂度，但是这些算法往往都是有局限性的，并不能适用于各种不同的抽象图数据，这便对Theta * 的应用场景产生了限制。于是，我们从另外一个角度来考虑这个问题，即减少LOS的次数以提升效率，也就是Lazy Theta * 。

Theta * 在每次扩展到一个新的顶点s时，都会将所有s的可见邻接点都与parent(s)计算一次LOS,然后更新这些邻接点的g值和父节点，再将它们添加到 open list 中去，这导致每扩展一个点都要进行大量的LOS计算，特别是在3D网格中邻接点数量急剧增加的时候，而实际上并不是所有邻接点的LOS计算都是必要的，因为很多点最终并不会被访问到。

与Theta * 不同的是，Lazy Theta * 在扩展到一个新的顶点时，并不对邻接点的LOS进行计算，而是乐观地认为所有可见邻接点与parent(s)都存在LOS，于是直接修改它们的g值和父节点，然后添加到open list中去。当从open list 中pop出某个顶点，需要真正以这个顶点为基础开始扩展的时候，再去验证它与父节点之间是否真的存在LOS，如果存在，则什么也不用改变，如果不存在，则重新计算它的g值和父节点。这样，只有那些真正被探索到的点才会实际执行LOS检查，大大减少了LOS的次数。

假设要重新计算g值和父节点的顶点为s’，计算方法是：

• 找到s’的可见邻接点s’’
• 如果 s’’ 不在close list 中，则舍弃
• 如果s’’ 在close list 中，则计算 g = g(s’’) + c(s’ , s’’)
• 取最终g最小的那个s’’，即为s’的父节点，其对应算出的 g 值即为s’的 g 值

之所以这么做，是因为我们确信，一定存在这样的一个顶点s’’，正是因为这个s’'的存在，所以当前点s’才会被添加进open list 当中。

Lazy Theta * 的核心伪代码如下图。

图 5：

在实际运用中，特别是在3D空间下，Lazy Theta * 可以大幅度地降低LOS检查的次数（如下图）。

图 6：

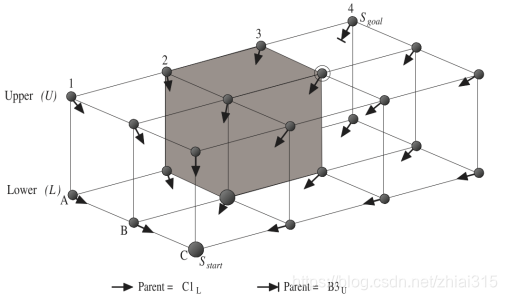
上图中，从C_1L到 A_4U 的寻路过程中，Theta * 算法会执行36次LOS检测，而Lazy Theta * 只会执行4次。

8. Lazy Theta * 的变体

本节介绍两种Lazy Theta * 的变体，仅供参考。

8.1 Lazy Theta * -R

Lazy Theta * -R 与 Lazy Theta * 基本相同，其唯一不同的地方在于，在 Lazy Theta * -R中，当某个点的LOS检测没有通过时，除了对其重新计算g值和父节点之外，还会对其进行标记，并在计算结束之后将其重新放回open list 中，然后重新pop。
这样做的目的是使用路径1重新检查路径，以确保获取到的路径是最短路径，因为如果不把点放回open list中，那g值就是不可变的了。

8.2 Lazy Theta * -P

与 Lazy Theta * 的乐观性不同，每当扩展到一个新的顶点 s 的时候，Lazy Theta * -P 总是悲观的认为 s 的所有邻接点 s’ 都与parent(s)之间不存在LOS，于是它会按照路径1设置s’的 g 值和父节点。Lazy Theta * -P 之所以如此做，其背后的思想是这样可以携带一个重要的属性，也就是保证在open list 中的所有顶点，与其父节点之间一定是存在LOS的。这在一些特殊情况下是有用的。