MATLAB实时脚本分析系统的类冲激响应，并绘制伯德图

本文主要是介绍MATLAB实时脚本分析系统的类冲激响应，并绘制伯德图，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目的

这里使用自动驾驶车的转向角度作为输入模拟冲激信号
输出分别为：横向加速度，yaw rate和推定的侧滑角
通过对输入和输出进行傅里叶变换，求出频域的比例关系后绘制伯德图。以观察车辆的传递特性
*由于包含数据的机密性分析结果就不放实际数据图片了，只是作为学习笔记分享一下代码的思路

1. 导入数据

使用CAN信号的记录文件并转换为.mat数据文件后进行分析，每一个数据对应了一个采样时间文件，其中的数据是一一对应的。

close all
clear variables%选择信号文件
filename = 'ImpulseSignal.mat';
load(filename);%测试用信号　V = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
S = VehicleSpeed_t1;            %车速（测试用）
StAngle = SteerAngle_t2;        %前轮方向转角（输入）
lAcc = Acc_t3;                  %横向加速度（输出）
Yaw = YawRate_t4;               %yaw rate（输出）
SlAngle = SlipAngle_t5;         %推定侧滑角度（输出）

1.1 参数设定

有效信号的分割点信息
我这里使用的是等间距的冲激信号作为输入，如下图所示，需要将每一个独立的信号分割后进行傅里叶分析

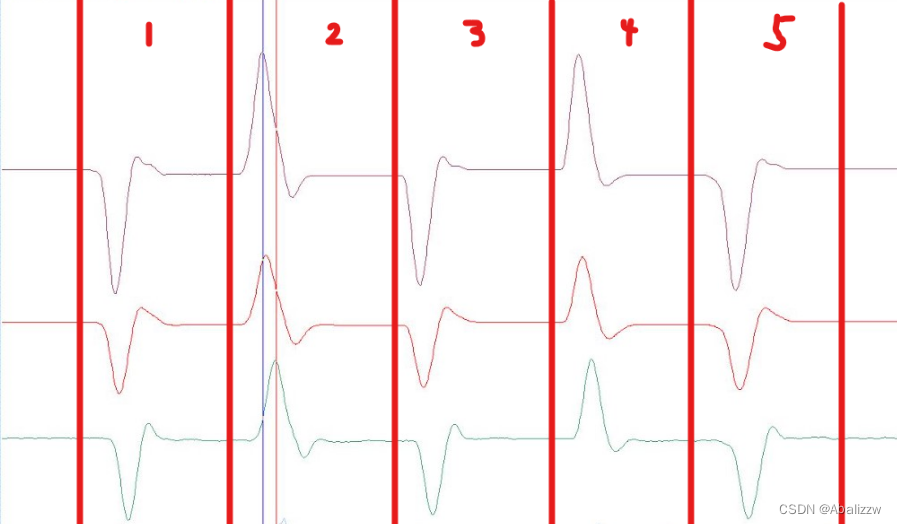
%有效信号的分割点信息
Seginfo_test = [350 240 3];               %[有效信号的起始点，冲激信号间隔，冲激信号总数]
Seginfo_1 = [];
seginfo = Seginfo_test;                   
n = seginfo(3);

读取数据部分和相应的时间戳部分，如果输入和输出的采样时间不一致需要将高频数据降采样处理。这里我的转向角输入t2和侧滑角输出t5的采样时间是其他信号的两倍，所以降采样使其保持一致。
为了生成预备数据，代码从这里开始执行到第二章FFT，直到最后全部数据生成后再向后执行。

Y_data = 'SlAngle'
if strcmp(Y_data,'StAngle')Y = downsample(StAngle,2);T = downsample(t2,2);dataid = 1;elseif strcmp(Y_data,'lAcc')Y = lAcc;T = t3;dataid = 2;elseif strcmp(Y_data,'Yaw')Y = Yaw;T = t4;dataid = 3;elseif strcmp(Y_data,'SlAngle')Y = downsample(SlAngle,2);T = downsample(t5,2);dataid = 4;
elseY = S;T = t2;dataid = 0;
endt_sample = mean(diff(T))    % Sampling perios/time
Fs = round(1/t_sample)      % Sampling frequency                    
L = size(Y,1)               % Length of signal

1.2 初始信号

plot(T(1:L),Y(1:L))         %绘制初始信号图
title("转向角")
xlabel("t (seconds)")
ylabel("S(t)")

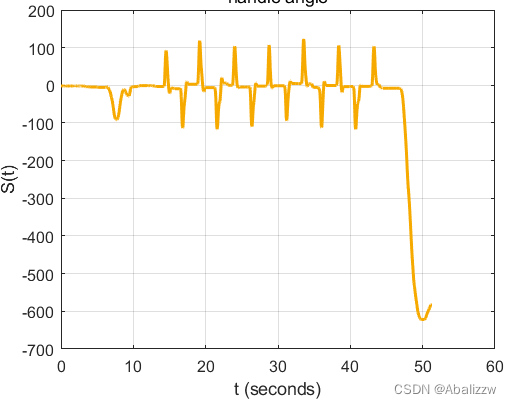
在这里插入图片描述

1.3 分割信号

%按照分割点的信息自动求出时间切片和对应的index
start_id=round(seginfo(1)/(t_sample/0.01));
interval=round(seginfo(2)/(t_sample/0.01));
for ii=1:nr=start_id+(ii-1)*interval:start_id+ii*interval-1;time_slice{ii}=T(r);time_index{ii}=(r)';
end

1.3a　有效信号部分样本


impulse_id=1;                                                   %选定N个有效冲激信号中的第impulse_id个绘制图形
%Y_m = mean(Y(time_index{impulse_id}))                          %信号取平均的两种方法
%Y_d = detrend(Y(time_index{impulse_id}), 0);
figure(1);
clf;
plot(time_slice{impulse_id},Y(time_index{impulse_id}),'--')     %绘制初始信号
hold on
plot(time_slice{impulse_id},Y(time_index{impulse_id})-Y_m)      %绘制取平均后的信号title(['handle angle ID:',num2str(impulse_id)])
xlabel("t (seconds)")
ylabel(['S',num2str(impulse_id),'(t)'])

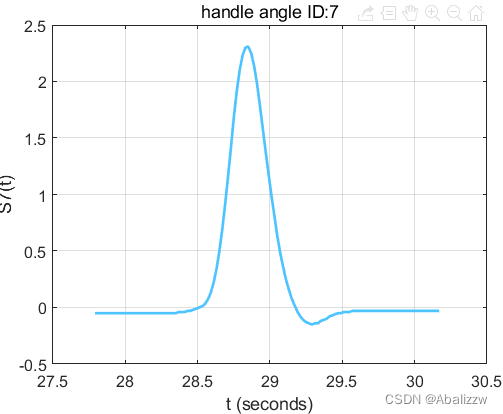
在这里插入图片描述

1.3b 生成全部的冲激信号切片，并按顺序保存

for ii=1:n%Ym = mean(Y(time_index{ii}));    %这里我不取平均了，因为对傅里叶分析的结果没有影响S_x{ii} = time_slice{ii};%S_y{ii} = Y(time_index{ii}-Y_m);S_y{ii} = Y(time_index{ii}); 
end

1.4 快速傅里叶变换(FFT, Fast Fourier Transform)

Sf=fft(S_y{impulse_id});              %FFT
Li = size(S_y{impulse_id},1)          %信号长度
P2 = Sf/Li;
P_Sf = P2(1:Li/2);
P_Sf(2:end-1) = 2*P_Sf(2:end-1);      %取前半部分数据

作图

figure(2);
clf;Px = (Fs*(0:(Li/2)-1)/Li)';             %根据奈奎斯特频率取(Fs/2)
plot(Px,P_Sf)
%xlim([0 Fs/2]);                       
%plot(Fs*(0:(Li/2))/Li,P1) 
title("Fast Fourier Transform of S(f)")
xlabel("f (Hz)")
ylabel(['FFT[S',num2str(impulse_id),'(t)]=S',num2str(impulse_id),'(f)'])

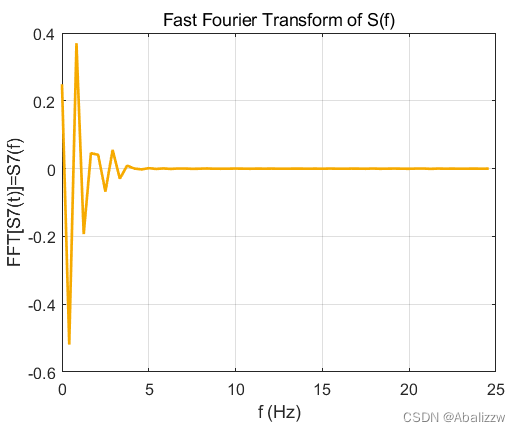
在这里插入图片描述

2.FFT数据生成

for x=1:nFFT = fft(S_y{x});L = size(S_y{x},1);FFT = FFT/L;FFT = FFT(1:L/2);FFT(2:end-1) = 2*FFT(2:end-1);if dataid == 1Res_StAngle{x} = FFT;            %转向角（输入）elseif dataid == 2Res_lAcc{x} = FFT;               %横向加速度（输出）elseif dataid == 3Res_Yaw{x} = FFT;                %Yawrate（输出）elseif dataid == 4Res_SlAngle{x} = FFT;            %侧滑角（输出）end
end

3.生成比例数据

输入和输出的比例反映了系统的响应特征，也就是传递函数
我们可以利用得到的特征数据和标准模型进行对比，从而观察出外界因素对系统响应的影响

for x=1:nRes_lAcc_R{x} = Res_lAcc{x}./Res_StAngle{x};Res_Yaw_R{x} = Res_Yaw{x}./Res_StAngle{x};Res_SlAngle_R{x} = Res_SlAngle{x}./Res_StAngle{x};
endRes_lAcc_sum = 0;
Res_Yaw_sum = 0;
Res_SlAngle_sum = 0;for i=1:n   Res_lAcc_sum = Res_lAcc_sum + Res_lAcc_R{i};Res_Yaw_sum = Res_Yaw_sum + Res_Yaw_R{i};Res_SlAngle_sum = Res_SlAngle_sum + Res_SlAngle_R{i};
end%计算所有冲激响应的均值
Res_lAcc_mean = Res_lAcc_sum/n;
Res_Yaw_mean = Res_Yaw_sum/n;
Res_SlAngle_mean = Res_SlAngle_sum/n;

4.結果

4.1　转向角（输入）→横向加速度（输出1）

*由于数据的机密性这里开始就不放图片了

figure(3);
clf;
ax = (Fs*(0:(Li/2)-1)/Li)';subplot(2,1,1);
semilogx(ax,20*log10(abs(Res_lAcc_mean))); grid on;
title("转向角→横向加速度")
%xlabel('f (Hz)')
ylabel('Gain[dB]')subplot(2,1,2);
semilogx(ax, 180/pi*angle(Res_lAcc_mean)); grid on;
xlabel('f (Hz)')
ylabel('相位[deg]')

4.2 转向角→yawrate（输出2）

figure(4);
clf;subplot(2,1,1);
semilogx(ax,20*log10(abs(Res_Yaw_mean))); grid on;
title("转向角→yawrate")
ylabel('Gain[dB]')
subplot(2,1,2);
semilogx(ax,180/pi*angle(Res_Yaw_mean)); grid on;
xlabel('f (Hz)')
ylabel('相位[deg]')

4.3 转向角→侧滑角（输出3）

figure(5);
clf;subplot(2,1,1);
semilogx(ax,20*log10(abs(Res_SlAngle_mean))); grid on;
title("转向角→侧滑角")
ylabel('Gain[dB]')subplot(2,1,2);
semilogx(ax,180/pi*angle(Res_SlAngle_mean)); grid on;
xlabel('f (Hz)')
ylabel('相位[deg]')