牛客-筛子游戏 (概率dp)

题目链接

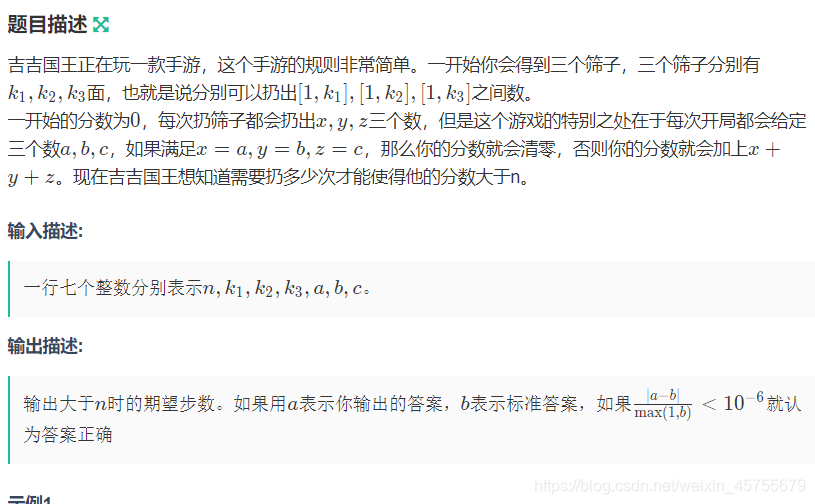
题解：
设 $dp[i]$ 表示当前分数为 $i$ 要达到目标的期望，则：

$dp[i]={\sum }_{k=3}^{k1+k2+k3}(p[k]\cdot dp[i+k])+p[0]\cdot dp[0]+1$,接下来的构造非常的妙。

设$dp[i]=a[i]\cdot dp[0]+b[i]$，那么式子可以变成：

$dp[i]={\sum }_{k=3}^{k1+k2+k3}(p[k]\cdot a[i+k]\cdot dp[0]+p[k]\cdot b[i+k])+p[0]\cdot dp[0]+1$

那么可以推出：$a[i]={\sum }_{k=3}^{k1+k2+k3}(p[k]\cdot a[i+k])+dp[0]$, $b[i]={\sum }_{k=3}^{k1+k2+k3}(p[k]\cdot b[i+k])+1$

根据递推式，就可以从后往前求出 $a[0]$ 和 $b[0]$ ,$dp[0]=b[0]/(1-a[0])$

代码

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<stack>
#include<set>
#include<ctime>
#define iss ios::sync_with_stdio(false)
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
typedef pair<int,int>pii;
const int MAXN=5e2+500;
const int mod=1004535809;
const int inf=0x3f3f3f3f;
double p[MAXN];
double aa[MAXN];
double bb[MAXN];
int main()
{int n,k1,k2,k3,a,b,c;cin>>n>>k1>>k2>>k3>>a>>b>>c;p[0]=1.0/(k1*k2*k3);for(int i=3;i<=k1+k2+k3;i++){int cnt=0;for(int t1=1;t1<=k1;t1++){for(int t2=1;t2<=k2;t2++){for(int t3=1;t3<=k3;t3++){if(t1==a&&t2==b&&t3==c) continue;if(t1+t2+t3==i) cnt++;}}}p[i]=1.0*cnt/(k1*k2*k3);}for(int i=n;i>=0;i--){for(int k=3;k<=k1+k2+k3;k++){aa[i]+=aa[i+k]*p[k];bb[i]+=p[k]*bb[i+k];}aa[i]+=p[0];bb[i]+=1.0;}double ans=bb[0]/(1-aa[0]);printf("%.8lf\n",ans);
}