J. Easy Integration (逆元分部积分) 2020牛客暑期多校训练营（第一场）

本文主要是介绍J. Easy Integration (逆元分部积分) 2020牛客暑期多校训练营（第一场），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

传送门
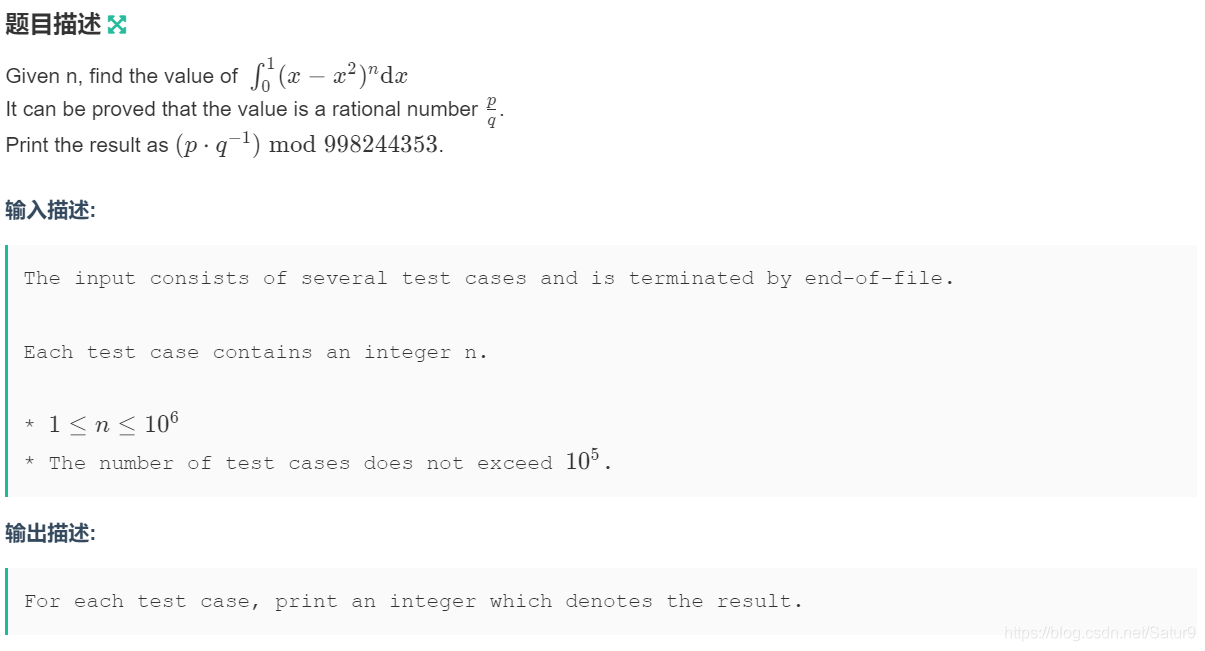
在这里插入图片描述

思路：

题意就是给你n，让求出下下列式子的结果：
很明显这就是数学方面的问题啦，这么菜的我在数学方面就更菜，反正最后看题解博客得知结果就是 (n)! / (2n+1)!。

代码实现：

#include<bits/stdc++.h>
//#define endl '\n'
#define null NULL
#define ll long long
#define int long long
#define pii pair<int, int>
#define lowbit(x) (x &(-x))
#define ls(x) x<<1
#define rs(x) (x<<1+1)
#define me(ar) memset(ar, 0, sizeof ar)
#define mem(ar,num) memset(ar, num, sizeof ar)
#define rp(i, n) for(int i = 0, i < n; i ++)
#define rep(i, a, n) for(int i = a; i <= n; i ++)
#define pre(i, n, a) for(int i = n; i >= a; i --)
#define IOS ios::sync_with_stdio(0); cin.tie(0);cout.tie(0);
const int way[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
using namespace std;
const int  inf = 0x7fffffff;
const double PI = acos(-1.0);
const double eps = 1e-6;
const int mod = 998244353;
const int N = 2e6 + 5;int n, f[N];int qmi(int a, int k){int res = 1;while(k){if(k & 1) res = (ll)res * a % mod;k >>= 1;a = (ll)a * a % mod;}return res%mod;
}void Inint(){f[1] = 1;for(int i = 2; i < N; i ++) f[i] = f[i-1]*i%mod;
}signed main() {IOS;Inint();while(cin >> n){ll x = f[n] * f[n] % mod, y = f[2*n+1];cout << x*qmi(y, mod-2)%mod << endl;}return 0;
}