我将建立道琼斯工业平均指数(DJIA)日交易量对数比的ARMA-GARCH模型。
获取数据
load(file='DowEnvironment.RData')
日交易量
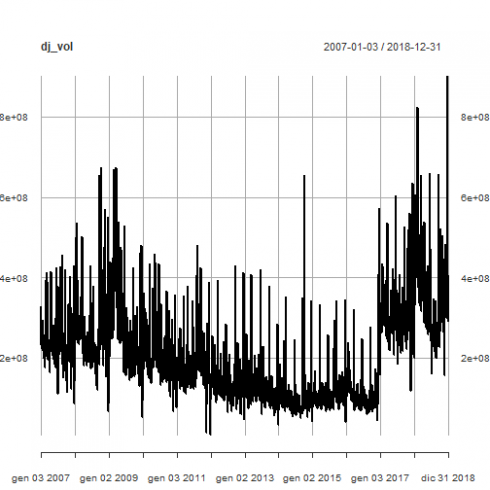
在第2部分中,我们已经强调了在每日交易量内发生的一些水平变化。
plot(dj_vol)
现在我们要确定并确定此类级别变化的日期。首先,我们验证具有常数均值的线性回归在统计上是显着的。
这种线性回归模型具有统计显着性,因此有必要继续进行关于恒定值的断点结构识别。
bp_dj_vol <- breakpoints(dj_vol ~ 1, h = 0.1)
summary(bp_dj_vol)
##
## Optimal(m + 1)段分区:
##
##致电:
## breakpoints.formula(formula = dj_vol~1,h = 0.1)
##
##观察编号的断点:
##
## m = 1 2499
## m = 2 896 2499
## m = 3 626 1254 2499
## m = 4 342 644 1254 2499
## m = 5 342 644 1219 1649 2499
## m = 6 320 622 924 1251 1649 2499
## m = 7 320 622 924 1251 1692 2172 2499
## m = 8 320 622 924 1251 1561 1863 2172 2499
##
##对应于breakdates:
##
## m = 1
## m = 2 0.296688741721854
## m = 3 0.207284768211921
## m = 4 0.113245033112583 0.213245033112583
## m = 5 0.113245033112583 0.213245033112583
## m = 6 0.105960264900662 0.205960264900662 0.305960264900662
## m = 7 0.105960264900662 0.205960264900662 0.305960264900662
## m = 8 0.105960264900662 0.205960264900662 0.305960264900662
##
## m = 1
## m = 2
## m = 3 0.41523178807947
## m = 4 0.41523178807947
## m = 5 0.40364238410596 0.546026490066225
## m = 6 0.414238410596027 0.546026490066225
## m = 7 0.414238410596027 0.560264900662252
## m = 8 0.414238410596027 0.516887417218543 0.616887417218543
##
## m = 1 0.827483443708609
## m = 2 0.827483443708609
## m = 3 0.827483443708609
## m = 4 0.827483443708609
## m = 5 0.827483443708609
## m = 6 0.827483443708609
## m = 7 0.719205298013245 0.827483443708609
## m = 8 0.719205298013245 0.827483443708609
##
##适合:
##
## m 0 1 2 3 4 5 6
## RSS 3.872e + 19 2.772e + 19 1.740e + 19 1.547e + 19 1.515e + 19 1.490e + 19 1.475e + 19
## BIC 1.206e + 05 1.196e + 05 1.182e + 05 1.179e + 05 1.178e + 05 1.178e + 05 1.178e + 05
##
## m 7 8
## RSS 1.472e + 19 1.478e + 19
## BIC 1.178e + 05 1.178e + 05
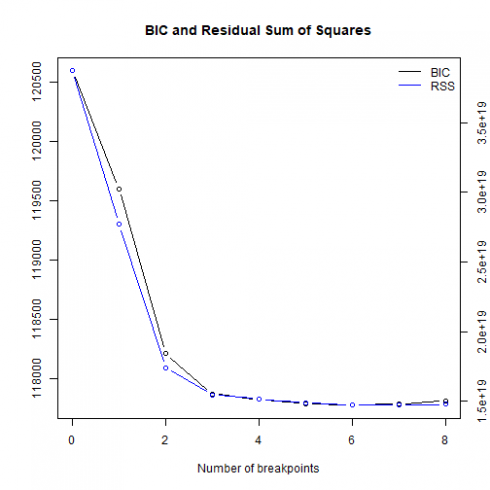
plot(bp_dj_vol)
在休息时间= 6时达到最小BIC。
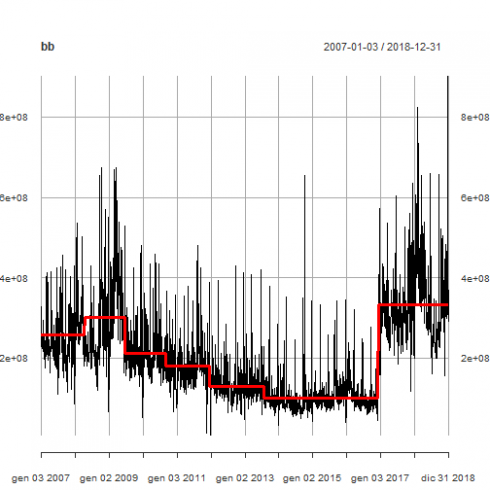
以下是道琼斯日均交易量与水平变化(红线)的情节。
plot(bb, lwd = c(3,1), col = c("red", "black"))
以下是发生此类级别转换的日历日期。
每日交易量对数比率模型
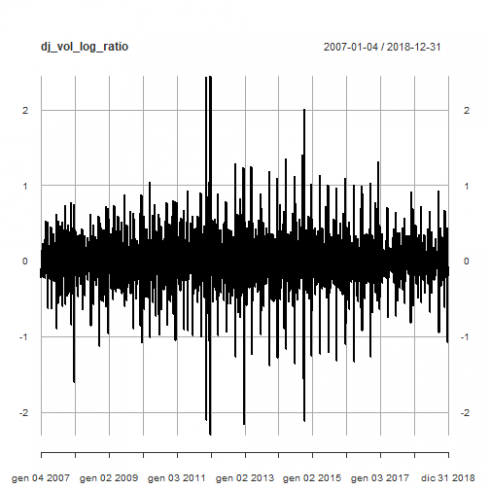
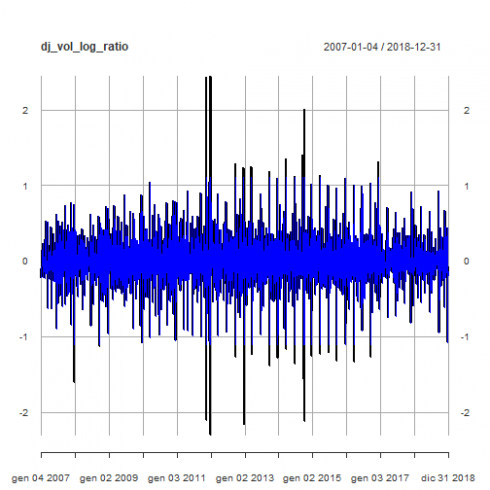
如第2部分所示,每日交易量对数比率:
plot(dj_vol_log_ratio)
异常值检测
Performance Analytics包中的Return.clean函数能够清除异常值的返回时间序列。下面我们将原始时间序列与调整后的异常值进行比较。
对原始时间序列进行分析的起诉将作为波动率评估的一种更保守的方法。
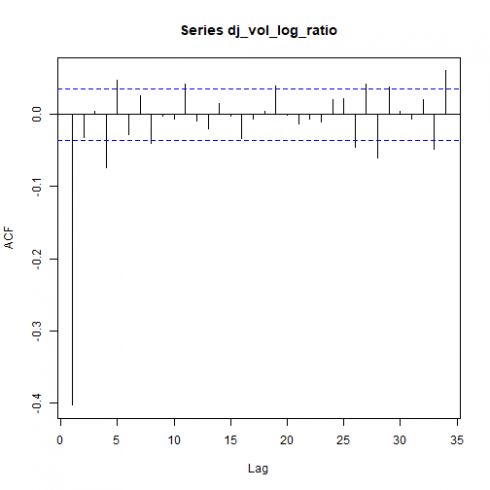
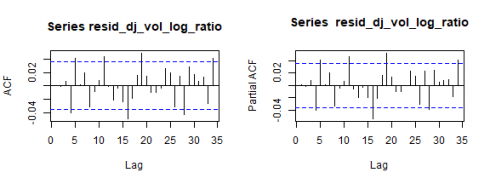
相关图
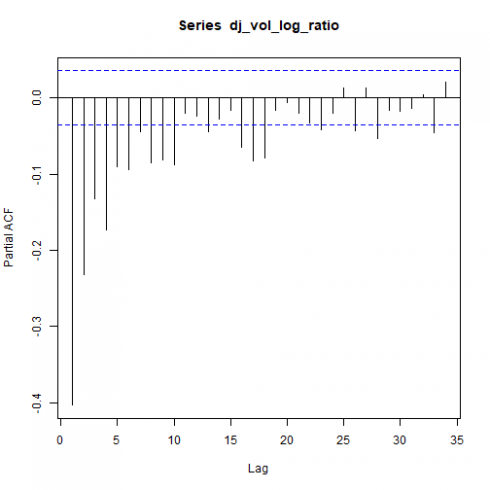
以下是总相关图和部分相关图。
pacf(dj_vol_log_ratio)
上图可能表明某些ARMA(p,q)模型的p和q> 0.这将在本分析的起诉范围内得到验证。
单位根测试
我们在urca包中提供Augmented Dickey-Fuller测试。
根据报告的测试统计数据与临界值进行比较,我们拒绝单位根存在的零假设。见参考。[6]有关Augmented Dickey-Fuller测试的更多详细信息。
ARMA模型
我们现在确定时间序列的ARMA结构,以便对结果残差运行ARCH效果测试。这与参考文献中概述的内容一致。[4] 4.3美元。
我们利用预测包中的auto.arima()函数(参考文献[7])来了解ARMA模型的开始。
ma1系数在统计上不显着。因此,我们尝试使用以下ARMA(2,3)模型。
(arma ## arima(x = dj_vol_log_ratio,order = c(2,0,3),include.mean = FALSE)
##
##系数:
## ar1 ar2 ma1 ma2 ma3
## -0.1802 0.6441 -0.4351 -0.8604 0.3596
## se 0.0643 0.0454 0.0681 0.0493 0.0423
##
## sigma ^ 2估计为0.0658:对数似然= -176.9,aic = 363.79
coeftest(arma_model_2)
##
## z系数测试:
##
## Estimate Std。误差z值Pr(> | z |)
## ar1 -0.180233 0.064315 -2.8023 0.005073 **
## ar2 0.644104 0.045449 14.1721 <2.2e-16 ***
## ma1 -0.435122 0.068126 -6.3870 1.692e-10 ***
## ma2 -0.860443 0.049282 -17.4595 <2.2e-16 ***
## ma3 0.359564 0.042307 8.4990 <2.2e-16 ***
## ---
## Signif。代码:0'***'0.001'**'0.01'*'0.05'。' 0.1''1
所有系数都具有统计显着性,AIC低于第一个模型。然后我们尝试使用ARMA(1,2)。
## arima(x = dj_vol_log_ratio,order = c(1,0,2),include.mean = FALSE)
##
##系数:
## ar1 ma1 ma2
## 0.6956 -1.3183 0.3550
## se 0.0439 0.0518 0.0453
##
## sigma ^ 2估计为0.06598:对数似然= -180.92,aic = 367.84
coeftest(arma_model_3)
##
## z系数测试:
##
## Estimate Std。误差z值Pr(> | z |)
## ar1 0.695565 0.043874 15.8537 <2.2e-16 ***
## ma1 -1.318284 0.051787 -25.4557 <2.2e-16 ***
## ma2 0.355015 0.045277 7.8409 4.474e-15 ***
## ---
## Signif。代码:0'***'0.001'**'0.01'*'0.05'。' 0.1''1
该模型在集合中具有最高的AIC,并且所有系数具有统计显着性。
我们还可以尝试使用eacf()TSA包中的功能作为进一步验证。
eacf(dj_vol_log_ratio)
## AR / MA
## 0 1 2 3 4 5 6 7 8 9 10 11 12 13
## 0 xooxxooxooxooo
## 1 xxoxoooxooxooo
## 2 xxxxooooooxooo
## 3 xxxxooooooxooo
## 4 xxxxxoooooxooo
## 5 xxxxoooooooooo
## 6 xxxxxoxooooooo
## 7 xxxxxooooooooo
以“O”为顶点的左上角三角形似乎位于{(1,2),(2,2),(1,3),(2,3)}之内,代表潜在的集合( p,q)根据eacf()函数输出的值。要注意我们更喜欢考虑简约模型,这就是为什么我们不要像AR和MA订单那样走得太远。
我们已经在集合{(3,2)(2,3)(1,2)}内验证了具有(p,q)阶的ARMA模型。让我们试试{(2,2)(1,3)}
## arima(x = dj_vol_log_ratio,order = c(2,0,2),include.mean = FALSE)
##
##系数:
## ar1 ar2 ma1 ma2
## 0.7174 -0.0096 -1.3395 0.3746
## se 0.1374 0.0560 0.1361 0.1247
##
## sigma ^ 2估计为0.06598:对数似然= -180.9,aic = 369.8
coeftest(arma_model_4)
##
## z系数测试:
##
## Estimate Std。误差z值Pr(> | z |)
## ar1 0.7173631 0.1374135 5.2205 1.785e-07 ***
## ar2 -0.0096263 0.0560077 -0.1719 0.863536
## ma1 -1.3394720 0.1361208 -9.8403 <2.2e-16 ***
## ma2 0.3746317 0.1247117 3.0040 0.002665 **
## ---
## Signif。代码:0'***'0.001'**'0.01'*'0.05'。' 0.1''1
ar2系数在统计上不显着。
( ## arima(x = dj_vol_log_ratio,order = c(1,0,3),include.mean = FALSE)
##
##系数:
## ar1 ma1 ma2 ma3
## 0.7031 -1.3253 0.3563 0.0047
## se 0.0657 0.0684 0.0458 0.0281
##
## sigma ^ 2估计为0.06598:对数似然= -180.9,aic = 369.8
coeftest(arma_model_5)
##
## z系数测试:
##
## Estimate Std。误差z值Pr(> | z |)
## ar1 0.7030934 0.0656902 10.7032 <2.2e-16 ***
## ma1 -1.3253176 0.0683526 -19.3894 <2.2e-16 ***
## ma2 0.3563425 0.0458436 7.7730 7.664e-15 ***
## ma3 0.0047019 0.0280798 0.1674 0.867
## ---
## Signif。代码:0'***'0.001'**'0.01'*'0.05'。' 0.1''1
ma3系数在统计上不显着。
作为结论,我们将ARMA(1,2)和ARMA(2,3)保持为暂定平均模型。我们现在可以继续进行ARCH效果测试。
ARCH效果测试
如果ARCH效应对于我们的时间序列的残差具有统计显着性,则需要GARCH模型。
我们测试候选平均模型ARMA(2,3)。
##
## ARCH LM-test; 空假设:没有ARCH效应
##
## data:resid_dj_vol_log_ratio - mean(resid_dj_vol_log_ratio)
##卡方= 78.359,df = 12,p值= 8.476e-12
根据报告的p值,我们拒绝无ARCH效应的零假设。
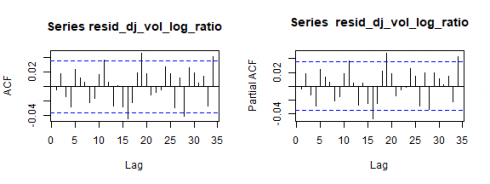
让我们看一下残差相关图。
par(mfrow=c(1,2))
acf(resid_dj_vol_log_ratio)
pacf(resid_dj_vol_log_ratio)
我们测试了第二个候选平均模型ARMA(1,2)。
re ## ARCH LM-test; 空假设:没有ARCH效应
##
## data:resid_dj_vol_log_ratio - mean(resid_dj_vol_log_ratio)
##卡方= 74.768,df = 12,p值= 4.065e-11
根据报告的p值,我们拒绝无ARCH效应的零假设。
让我们看一下残差相关图。
par(mfrow=c(1,2))
acf(resid_dj_vol_log_ratio)
pacf(resid_dj_vol_log_ratio)
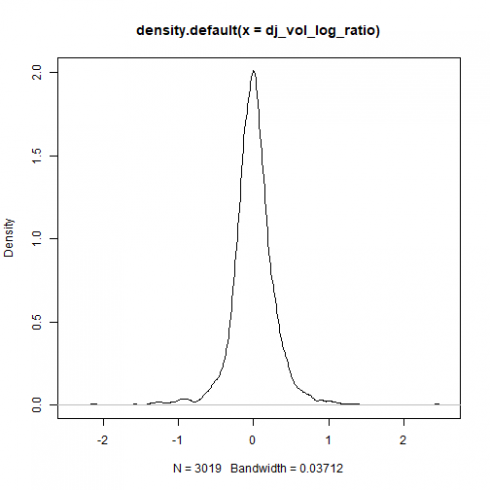
要检查DJIA体积对数比率内的不对称性,将显示汇总统计数据和密度图。
## DJI.Volume
## nobs 3019.000000
## NAs 0.000000
##最低-2.301514
##最大2.441882
## 1. Quartile -0.137674
## 3.四分位数0.136788
##平均值-0.000041
##中位数-0.004158
## Sum -0.124733
## SE平均值0.005530
## LCL平均值-0.010885
## UCL平均值0.010802
##差异0.092337
## Stdev 0.303869
## Skewness -0.182683
## Kurtosis 9.463384
plot(density(dj_vol_log_ratio))
因此,对于每日交易量对数比,还将提出eGARCH模型。
为了将结果与两个候选平均模型ARMA(1,2)和ARMA(2,3)进行比较,我们进行了两次拟合
ARMA-GARCH:ARMA(1,2)+ eGARCH(1,1)
##最佳参数
## ------------------------------------
## Estimate Std。误差t值Pr(> | t |)
## ar1 0.67731 0.014856 45.5918 0.0e + 00
## ma1 -1.22817 0.000038 -31975.1819 0.0e + 00
## ma2 0.27070 0.000445 608.3525 0.0e + 00
## omega -1.79325 0.207588 -8.6385 0.0e + 00
## alpha1 0.14348 0.032569 4.4053 1.1e-05
## beta1 0.35819 0.073164 4.8957 1.0e-06
## gamma1 0.41914 0.042252 9.9199 0.0e + 00
## skew 1.32266 0.031528 41.9518 0.0e + 00
##形状3.54346 0.221750 15.9795 0.0e + 00
##
##强大的标准错误:
## Estimate Std。误差t值Pr(> | t |)
## ar1 0.67731 0.022072 30.6859 0.0e + 00
## ma1 -1.22817 0.000067 -18466.0626 0.0e + 00
## ma2 0.27070 0.000574 471.4391 0.0e + 00
## omega -1.79325 0.233210 -7.6894 0.0e + 00
## alpha1 0.14348 0.030588 4.6906 3.0e-06
## beta1 0.35819 0.082956 4.3178 1.6e-05
## gamma1 0.41914 0.046728 8.9698 0.0e + 00
## skew 1.32266 0.037586 35.1902 0.0e + 00
##形状3.54346 0.238225 14.8744 0.0e + 00
##
## LogLikelihood:347.9765
##
##信息标准
## ------------------------------------
##
## Akaike -0.22456
## Bayes -0.20664
## Shibata -0.22458
## Hannan-Quinn -0.21812
##
##标准化残差的加权Ljung-Box检验
## ------------------------------------
##统计p值
##滞后[1] 0.5812 4.459e-01
##滞后[2 *(p + q)+(p + q)-1] [8] 8.5925 3.969e-08
##滞后[4 *(p + q)+(p + q)-1] [14] 14.1511 4.171e-03
## dof = 3
## H0:无序列相关
##
##标准化平方残差的加权Ljung-Box检验
## ------------------------------------
##统计p值
##滞后[1] 0.4995 0.4797
## Lag [2 *(p + q)+(p + q)-1] [5] 1.1855 0.8164
## Lag [4 *(p + q)+(p + q)-1] [9] 2.4090 0.8510
## dof = 2
##
##加权ARCH LM测试
## ------------------------------------
##统计形状比例P值
## ARCH Lag [3] 0.4215 0.500 2.000 0.5162
## ARCH Lag [5] 0.5974 1.440 1.667 0.8545
## ARCH Lag [7] 1.2835 2.315 1.543 0.8636
##
## Nyblom稳定性测试
## ------------------------------------
##联合统计:5.2333
##个人统计:
## ar1 0.63051
## ma1 1.18685
## ma2 1.11562
## omega 2.10211
## alpha1 0.08261
## beta1 2.07607
## gamma1 0.15883
## skew 0.33181
##形状2.56140
##
##渐近临界值(10%5%1%)
##联合统计:2.1 2.32 2.82
##个人统计:0.35 0.47 0.75
##
##签名偏差测试
## ------------------------------------
## t-value prob sig
## Sign Bias 1.600 0.10965
##负符号偏差0.602 0.54725
## Positive Sign Bias 2.540 0.01115 **
##联合效应6.815 0.07804 *
##
##
##调整Pearson拟合优度测试:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 20.37 0.3726
## 2 30 36.82 0.1510
## 3 40 45.07 0.2328
## 4 50 52.03 0.3567
##
##
##经过的时间:1.364722
所有系数都具有统计显着性。然而,基于上面报道的标准化残差p值的加权Ljung-Box检验,我们拒绝了对于本模型没有残差相关性的零假设。因此,模型ARMA(1,2)+ eGARCH(1,1)无法捕获我们时间序列的所有结构。
ARMA-GARCH:ARMA(2,3)+ eGARCH(1,1)
##
## * --------------------------------- *
## * GARCH模型适合*
## * --------------------------------- *
##
##条件方差动力学
## -----------------------------------
## GARCH型号:eGARCH(1,1)
##平均型号:ARFIMA(2,0,3)
##发行:sstd
##
##最佳参数
## ------------------------------------
## Estimate Std。误差t值Pr(> | t |)
## ar1 -0.18607 0.008580 -21.6873 0.0e + 00
## ar2 0.59559 0.004596 129.5884 0.0e + 00
## ma1 -0.35619 0.013512 -26.3608 0.0e + 00
## ma2 -0.83010 0.004689 -177.0331 0.0e + 00
## ma3 0.26277 0.007285 36.0678 0.0e + 00
## omega -1.92262 0.226738 -8.4795 0.0e + 00
## alpha1 0.14382 0.033920 4.2401 2.2e-05
## beta1 0.31060 0.079441 3.9098 9.2e-05
## gamma1 0.43137 0.043016 10.0281 0.0e + 00
## skew 1.32282 0.031382 42.1523 0.0e + 00
##形状3.48939 0.220787 15.8043 0.0e + 00
##
##强大的标准错误:
## Estimate Std。误差t值Pr(> | t |)
## ar1 -0.18607 0.023940 -7.7724 0.000000
## ar2 0.59559 0.022231 26.7906 0.000000
## ma1 -0.35619 0.024244 -14.6918 0.000000
## ma2 -0.83010 0.004831 -171.8373 0.000000
## ma3 0.26277 0.030750 8.5453 0.000000
## omega -1.92262 0.266462 -7.2154 0.000000
## alpha1 0.14382 0.032511 4.4239 0.000010
## beta1 0.31060 0.095329 3.2582 0.001121
## gamma1 0.43137 0.047092 9.1602 0.000000
## skew 1.32282 0.037663 35.1225 0.000000
##形状3.48939 0.223470 15.6146 0.000000
##
## LogLikelihood:356.4994
##
##信息标准
## ------------------------------------
##
## Akaike -0.22888
## Bayes -0.20698
## Shibata -0.22891
## Hannan-Quinn -0.22101
##
##标准化残差的加权Ljung-Box检验
## ------------------------------------
##统计p值
##滞后[1] 0.7678 0.38091
## Lag [2 *(p + q)+(p + q)-1] [14] 7.7336 0.33963
## Lag [4 *(p + q)+(p + q)-1] [24] 17.1601 0.04972
## dof = 5
## H0:无序列相关
##
##标准化平方残差的加权Ljung-Box检验
## ------------------------------------
##统计p值
##滞后[1] 0.526 0.4683
## Lag [2 *(p + q)+(p + q)-1] [5] 1.677 0.6965
## Lag [4 *(p + q)+(p + q)-1] [9] 2.954 0.7666
## dof = 2
##
##加权ARCH LM测试
## ------------------------------------
##统计形状比例P值
## ARCH Lag [3] 1.095 0.500 2.000 0.2955
## ARCH Lag [5] 1.281 1.440 1.667 0.6519
## ARCH Lag [7] 1.940 2.315 1.543 0.7301
##
## Nyblom稳定性测试
## ------------------------------------
##联合统计:5.3764
##个人统计:
## ar1 0.12923
## ar2 0.20878
## ma1 1.15005
## ma2 1.15356
## ma3 0.97487
## omega 2.04688
## alpha1 0.09695
## beta1 2.01026
## gamma1 0.18039
## skew 0.38131
## shape 2.40996
##
##渐近临界值(10%5%1%)
##联合统计:2.49 2.75 3.27
##个人统计:0.35 0.47 0.75
##
##签名偏差测试
## ------------------------------------
## t-value prob sig
## Sign Bias 1.4929 0.13556
##负符号偏差0.6317 0.52766
## Positive Sign Bias 2.4505 0.01432 **
##联合效应6.4063 0.09343 *
##
##
##调整Pearson拟合优度测试:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 17.92 0.5278
## 2 30 33.99 0.2395
## 3 40 44.92 0.2378
## 4 50 50.28 0.4226
##
##
##经过的时间:1.660402
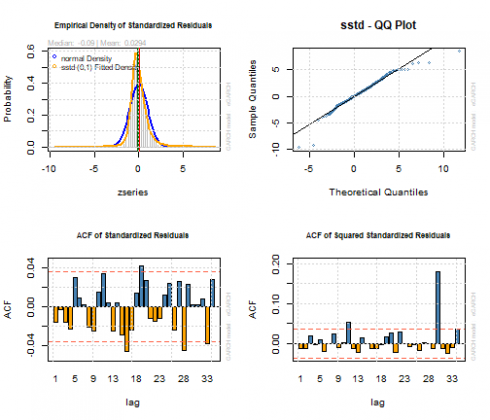
所有系数都具有统计显着性。没有找到标准化残差或标准化平方残差的相关性。模型可以正确捕获所有ARCH效果。调整后的Pearson拟合优度检验不拒绝零假设,即标准化残差的经验分布和所选择的理论分布是相同的。然而:
*对于其中一些模型参数随时间变化恒定的Nyblom稳定性测试零假设被拒绝
par(mfrow=c(2,2))
plot(garchfit, which=8)
plot(garchfit, which=9)
plot(garchfit, which=10)
plot(garchfit, which=11)
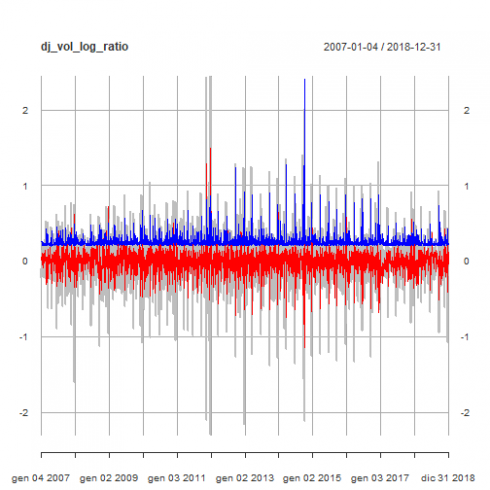
我们用平均模型拟合(红线)和条件波动率(蓝线)显示原始道琼斯日均交易量对数时间序列。
对数波动率分析
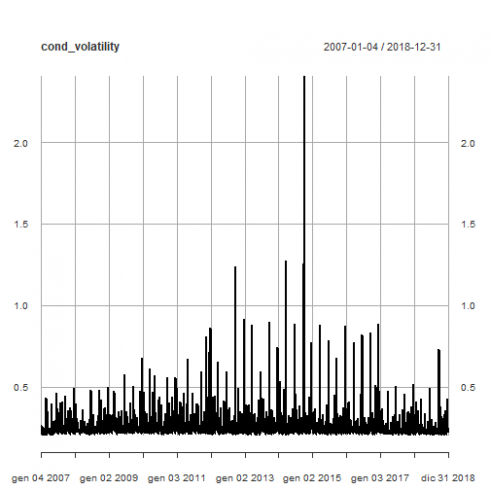
以下是我们的模型ARMA(2,2)+ eGARCH(1,1)产生的条件波动率图。
plot(cond_volatility)
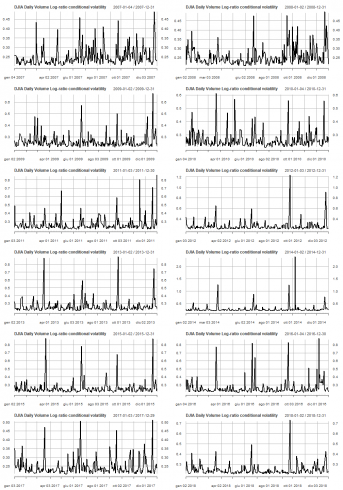
显示了按年度的条件波动率的线图。
par(mfrow=c(6,2))
pl <- lapply(2007:2018, function(x) { plot(cond_volatility[as.character(x)], main = "DJIA Daily Volume Log-ratio conditional volatility")})
pl
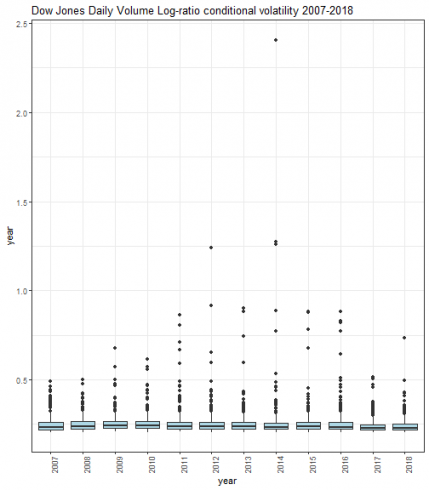
显示了按年度计算的条件波动率框图。
结论
我们介绍了摘要,线图和箱形图,以突出多年来的回报和交易量变化。
我们研究了基本统计指标,如平均值,偏差,偏度和峰度,以了解多年来价值观的差异,以及价值分布对称性和尾部。从这些摘要开始,我们获得了平均值,中位数,偏度和峰度指标的有序列表,以更好地突出多年来的差异。
箱形图允许理解分析中的样品的统计分散
密度图可以了解我们的经验样本分布的不对称性和尾部性。
对于对数回报和体积对数比,我们构建了ARMA-GARCH模型(指数GARCH,特别是作为方差模型),以获得条件波动率。同样,可视化作为线和框图突出显示了年内和年之间的条件波动率变化。这种调查的动机是,波动率是变化幅度的指标,用简单的词汇表示,并且是应用于资产的对数收益时的基本风险度量。有几种类型的波动性(有条件的,隐含的,实现的波动率)。见参考。详情请参阅图4和图8。
交易量可以被解释为衡量市场活动幅度和投资者兴趣的指标。计算交易量指标(包括波动率)可以了解这种活动/利息水平如何随时间变化。
非常感谢您阅读本文,有任何问题请联系我们!
大数据部落 -中国专业的第三方数据服务提供商,提供定制化的一站式数据挖掘和统计分析咨询服务
统计分析和数据挖掘咨询服务:y0.cn/teradat(咨询服务请联系官网客服)
【服务场景】
科研项目; 公司项目外包;线上线下一对一培训;数据采集;学术研究;报告撰写;市场调查。
【大数据部落】提供定制化的一站式数据挖掘和统计分析咨询