【算法基础】NSGA-II:非支配排序遗传算法

NSGA原文： Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms | MIT Press Journals & Magazine | IEEE Xplore

NSGA-II原文： A fast and elitist multiobjective genetic algorithm: NSGA-II

NSGA-II作者实验室：Kalyanmoy Deb, Koenig Endowed Chair Professor

pymoo库：实验室创建的python第三方库，实现了各种多目标优化算法pymoo: Multi-objective Optimization in Python

geatpy2库：Geatpy是一个高性能实用型进化算法工具箱，提供许多已实现的进化算法中各项重要操作的库函数​​​​​​​，利用“定义问题类 + 调用算法模板”的模式来进行进化优化，可用于求解单目标优化、多目标优化、复杂约束优化、组合优化、混合编码进化优化等 Geatpy

1. 背景：

1） NSGA有以下问题

• 非支配排序时间复杂度太高，为O(MN³)，其中M为多目标数，N为种群数
• 缺少精英保留策略(elitism)，研究表明精英策略能提高GA的性能
• 需要指定共享参数(share parameter)来确保种群多样性

NSGA-II是对NSGA的优化：

• 复杂度变为O(MN²)
• 有精英保留策略
• 拥挤度替代共享参数

2. 快速非支配排序

对解集进行pareto前沿分级，成Rank1、Rank2…

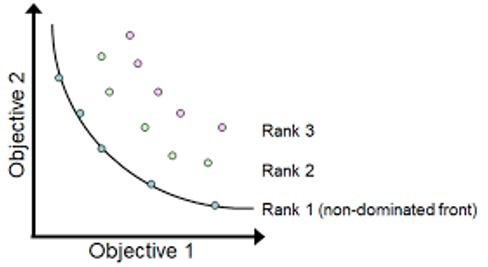
快速非支配排序将总时间复杂度降到了O(MN²)
空间复杂度O(N²)。

n_p：支配数，支配解p的解数量
S_P：被支配集合，解p支配的解集合
F_i：第i层Pareto前沿

3. 多样性保护 NSGA-II拥挤度比较

1) 密度估计

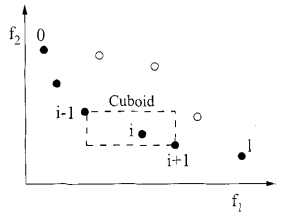
以下图片描述不太理解：

几何角度理解拥挤距离：
以两个目标函数为例，下图中黑点和白点分别为两个非支配前沿
对于解i，从与i在同一非支配前沿中选择与解i最相近的两个点i-1和i+1为顶点组成一个长方形(cuboid)
拥挤距离即为长方形周长

2）拥挤度比较算子

在计算完每个解的拥挤距离后，从一定程度上来说，某个解的拥挤距离越小，这个解被其他解拥挤的程度越高。

• 通过拥挤度比较算子，来选择解实现更广的帕累托最优解分布。
  种群中的每个个体都有两个属性：
  （1）非支配等级i_rank：1是最高等级
  （2）拥挤距离i_distance
  比较顺序：不同非支配等级的两个解，倾向于选择rank值更低的解
  如果两个解的等级相同，倾向于选择拥挤距离更大或者说拥挤区域更小的解。（防止陷入局补最优？）

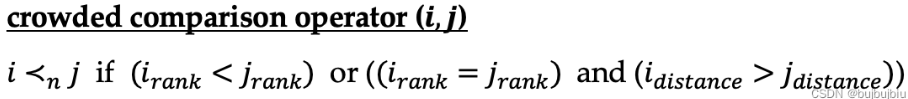
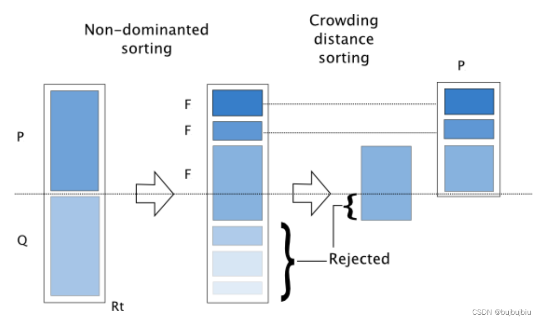
4. 主循环

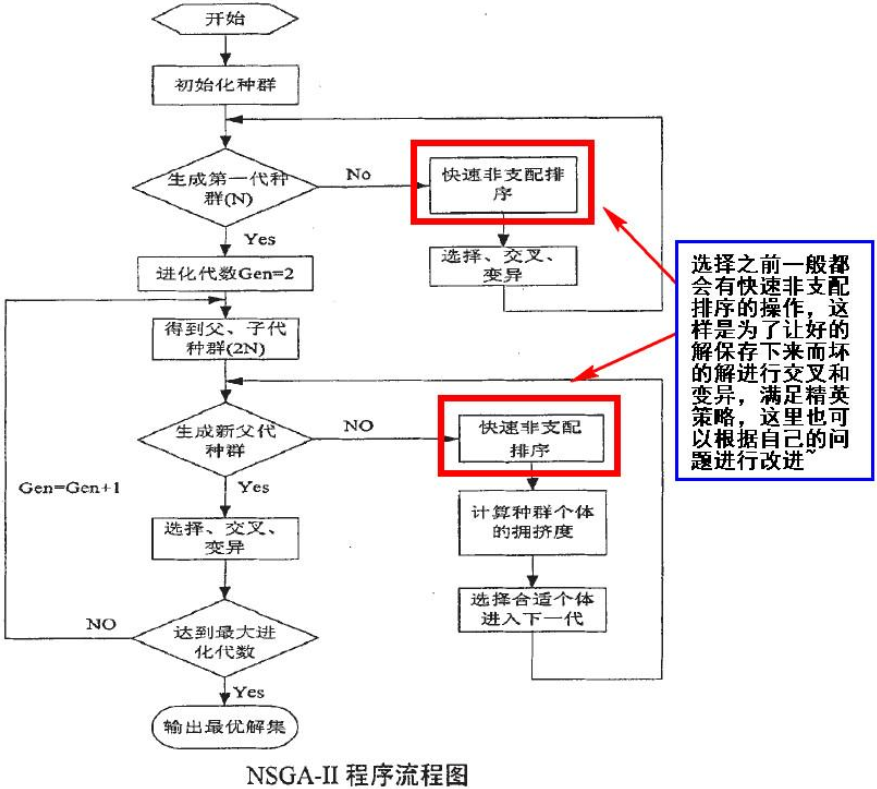
5. 其它概念：

elitism 精英保留策略：核心思想是把群体在进化过程中迄今出现的最好个体不进行遗传操作而直接复制到下一代中，理论上证明了具有精英保留的标准遗传算法是全局收敛的
tournament selection 联赛选择算法：每次从种群中取一定数量（n）的个体(放回抽样)，选择其中适应度较好的进入子代种群

https://blog.csdn.net/weixin_45526117/article/details/128507020