数据结构课程设计---马踏棋盘（C++）

2023-10-31 01:59
文章标签 c++ 数据结构 棋盘 课程设计 马踏

本文主要是介绍数据结构课程设计---马踏棋盘（C++），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

一、实验题目

二、数据结构设计

（一）存储结构设计

（二）结点结构设计

三、算法设计

（一）函数设计

    1.方法一：深度优先遍历（递归）

    2.方法二：深度优先遍历+贪心算法（递归）

    3.方法三：深度优先遍历+贪心算法（非递归）

    4.menu（）函数

（二）算法描述

四、完整代码

五、测试与运行

1.菜单

2.第一种方法求解

3.第二种方法求解

4.第三种方法求解

一、实验题目

    马踏棋盘：设计一个国际象棋的马踏遍棋盘的演示程序。将马随机放在国际象棋 8x8 棋盘 Board[8][8]的某个方格中，马按走棋规则进行移动。要求每个方格只进入一次，走遍棋盘上全部 64 个方格。编制递归或非递归程序，求出马的行走路线，并按求出的行走路线输出。

    结果中输出：在方阵中输出 1-64 个行走足迹。

二、数据结构设计

（一）存储结构设计

    马踏棋盘问题的处理，在设计时注重对于顺序遍历的考虑，不需要涉及插入和删除操作，因此采用顺序表存储。设置一个容量为64的Adr_Stack[MAX_STEPS]（ MAX_STEPS=64），通过其存储马的行走轨迹。

（二）结点结构设计

    本设计中一条记录中涉及着较多的数据项，因此需要单独对数据域进行自定义变量类型。类型HORSE_CHESS_STACK中共存储三个数据项：x_adr为横轴坐标，y_adr为纵轴坐标，direction是运动的方向。

typedef struct stack{int x_adr;     int y_adr;   int direction;}HORSE_CHESS_STACK;HORSE_CHESS_STACK Adr_Stack[64];

三、算法设计

    马踏棋盘问题，既可以递归处理，也可以非递归处理。在设计时，采取三种方式求解，第一种为深度优先遍历递归求解，第二种为在深度优先遍历的基础上加入贪心算法求解递归求解，第三种为在深度优先遍历的基础上加入贪心算法求解非递归求解。

（一）函数设计

    本设计中一共涉及十三个函数，通过这十三个函数的相互调用，实现马踏棋盘问题的求解。

    1.方法一：深度优先遍历（递归）

    第一种方法只需一个函数，Dfs（）函数用来求解深度优先遍历递归求解；

//深度优先遍历（递归）
void Dfs( int path[8][8], int m, int n, int edge, int count)
{if (count >= edge*edge) return;if (m <= edge-1 && n <= edge-1 && m >= 0 && n >= 0 && path[m][n] == 0){count++; path[m][n] = count; for (int i = 0;i < edge;i++)Dfs(path, m + move_x[i], n + move_y[i], edge, count); return;}elsereturn;
}

    2.方法二：深度优先遍历+贪心算法（递归）

    第二种方法也只需一个函数，Dfs_tx（）函数用来求解深度优先遍历加贪心算法递归求解；

//深度优先遍历+贪心算法（递归）
void Dfs_tx(int flag[8][8], int path[8][8], int m, int n, int edge, int count, int found)
{if(found)return;if(count >= edge*edge){found += 1; for(int i = 0; i < edge; i++){for(int j = 0; j < edge; j++)path[i][j] = flag[i][j];}return;}if(m > edge-1 || n > edge-1 || m < 0 || n < 0 || flag[m][n] != 0) return; count++; flag[m][n] = count; int count_next[8] = {-1,-1,-1,-1,-1,-1,-1,-1};for (int i = 0; i < edge; i++){int m_next = m + move_x[i];int n_next = n + move_y[i];     if (m_next < edge && n_next < edge && m_next >= 0 && n_next >= 0 && flag[m_next][n_next] == 0){count_next[i] ++;for (int j = 0; j < edge; j++){int m_next_next = m_next + move_x[j];int n_next_next = n_next + move_y[j];if (m_next_next < edge && n_next_next < edge && m_next_next >= 0 && n_next_next >= 0 && flag[m_next_next][n_next_next] == 0)                count_next[i]++;}}       }int opt_direct = 0;for (int i = 0; i < edge; i++){if (count_next[opt_direct] == -1)opt_direct = i;if ((count_next[i] < count_next[opt_direct]) && count_next[i] != -1){opt_direct = i;}}Dfs_tx( flag, path, m + move_x[opt_direct], n + move_y[opt_direct], edge, count, found); flag[m][n] = 0;                
}

    3.方法三：深度优先遍历+贪心算法（非递归）

    第三种方法涉及九个函数，首先是init（）函数，对顺序表进行初始化操作；然后是print_stack（）函数将栈中的情况输出以检验结果的正确性；第三第四个函数是push_stack（）和pop_stack（）函数，进行进栈和出栈操作；第五个mark_chess（）是标记函数，用来标记马已经走过的地方；第六个print_chess_board（）函数是将解决路径输出；第七个print_steps（）是将每一步的横纵坐标输出，进而可以直观检验结果；第八个run_horse_tanxin（）函数是核心函数，对于马踏棋盘用深度优先遍历加贪心算法非递归的处理；最后一个Dfs_tx_zhan（）函数是对以上各个函数总的调用，共同实现深度优先遍历加贪心算法非递归方法对马踏棋盘问题的解决。

//深度优先遍历+贪心算法（非递归）
typedef struct stack
{int x_adr;      int y_adr;    int direction;
}HORSE_CHESS_STACK;
int chess[ROW+1][COL+1];
int dir[8][2] = {{2,-1},{-2,-1},{-2,1},{2,1},{1,-2},{-1,-2},{-1,2},{1,2}};
int top;
HORSE_CHESS_STACK Adr_Stack[MAX_STEPS];
int out_stack;
void init()
{int n = MAX_STEPS;while(n--){Adr_Stack[n].x_adr = 0;Adr_Stack[n].y_adr = 0;Adr_Stack[n].direction = -1;}Adr_Stack[0].x_adr = 0;Adr_Stack[0].y_adr = 0;Adr_Stack[0].direction = -1;for(int i = 1;i <= ROW;i++){for(int j = 1;j <= COL;j++){chess[ROW][COL] = 0;}}  top = -1;out_stack = 0;
}
void print_stack()
{cout<<"栈中情况:\n";for(int i = 0;i < MAX_STEPS;i++){printf("x:%d  y:%d direction = %d\n",Adr_Stack[i].y_adr,Adr_Stack[i].x_adr,Adr_Stack[i].direction);}cout<<"\n\n";
}
void push_stack(int x_real,int y_real)
{top++;Adr_Stack[top].x_adr = x_real;Adr_Stack[top].y_adr = y_real;Adr_Stack[top].direction = -1; 
}
void pop_stack()
{Adr_Stack[top].x_adr = 0;Adr_Stack[top].y_adr = 0;Adr_Stack[top].direction = -1; top--;
}
void mark_chess(int x,int y)
{chess[y][x] = top + 1;
}
void print_chess_board()
{cout<<"\t\t\troute:"<<endl;for(int i = 1;i <= ROW;i++){cout<<"\t\t\t";for(int j = 1;j <= ROW;j++){printf("%4d ",chess[i][j]);}cout<<endl;}cout<<endl;
}
int t = 1;
void print_steps()
{printf("(%d,%d)",Adr_Stack[top].y_adr,Adr_Stack[top].x_adr);t++;if(t == ROW){cout<<endl;t = 0;}
}
void run_horse_tanxin()
{int x_now,y_now;while(1){if(top >= MAX_STEPS - 1){print_chess_board();break;}x_now = Adr_Stack[top].x_adr;y_now = Adr_Stack[top].y_adr;int next[ROW] = {};for(int i = 0;i < ROW;i++){int x_next = x_now + dir[i][0];int y_next = y_now + dir[i][1];if((x_next > 0 && x_next <= COL) && (y_next > 0 && y_next <= ROW) && chess[y_next][x_next] == 0 ){for(int j = 0;j < ROW;j++){int x_next_next = x_next + dir[j][0];int y_next_next = y_next + dir[j][1];if((x_next_next > 0 && x_next_next <= COL) && (y_next_next > 0 && y_next_next <= ROW) && chess[y_next_next][x_next_next] == 0){next[i]++;}}}}int real_next[8] = {0};int k = 0;int t = ROW + 1;for(int i = 0;i < ROW;i++){t = ROW + 1;for(int j = 0;j < 8;j++){if(next[j] < t){real_next[i] = j;t = next[j];k = j;}}next[k] = ROW + 1;}int dir_now = 0;for(dir_now = Adr_Stack[top].direction + 1;dir_now < ROW;dir_now++){int x_real = x_now + dir[real_next[dir_now]][0];int y_real = y_now + dir[real_next[dir_now]][1];Adr_Stack[top].direction += 1;if((x_real <= COL && x_real > 0) && (y_real <= ROW && y_real > 0) && chess[y_real][x_real] == 0){push_stack(x_real,y_real);mark_chess(x_real,y_real);break;}}if(Adr_Stack[top].direction >= 7){cout<<endl;printf("\n out:(%d,%d) \n",Adr_Stack[top].y_adr,Adr_Stack[top].x_adr);chess[Adr_Stack[top].y_adr][Adr_Stack[top].x_adr] = 0;out_stack++;pop_stack();}//print_stack(); print_steps();}
}
void Dfs_tx_zhan(int m,int n)
{init();push_stack(m,n);mark_chess(m,n);cout<<"\t\t\troute address:\n";printf("(%d,%d)",m,n);run_horse_tanxin();
}

    4.menu（）函数

    然后一个是menu（）函数，实现菜单功能，对三种方法进行调用；另一个是main（）主函数，进行输入操作，总体实现问题的求解。

void menu()
{system("cls");cout<<"\t\t\t马踏棋盘问题的解决："<<endl;cout<<"\t\t\t1.深度优先遍历（递归）"<<endl;cout<<"\t\t\t2.深度优先遍历+贪心算法结合（递归）"<<endl;cout<<"\t\t\t3.深度优先遍历+贪心算法结合(非递归）"<<endl;cout<<"\t\t\t0.退出"<<endl;cout<<"\t\t\t请输入选择：";int sel;cin>>sel;if (sel == 0)exit(0);while(sel >3 ||sel <0){cout <<"\t\t\t输入格式错误，请重新输入：";cin>>sel;}int m,n;int found = 0;int edge;cout<<"\t\t\t请输入棋盘的边长：";cin >> edge;cout<<"\t\t\t请输入初始时马的位置：";cin>>m >> n;int flag[8][8]={0};int path[8][8]={0};DWORD start = timeGetTime();if (sel == 1){cout <<"\t\t\t下面是采用深度优先遍历（递归）得出的结果："<<endl;Dfs( path, m, n, edge, 0);}else if (sel == 2){cout <<"\t\t\t下面是采用深度优先遍历+贪心算法结合（递归）得出的结果："<<endl;Dfs_tx( flag, path, m, n, edge, 0, found);}else if (sel == 3){cout<<endl;cout <<"\t\t\t下面是采用深度优先遍历+贪心算法结合（非递归）得出的结果："<<endl;Dfs_tx_zhan(m, n);}if (sel !=3){for (int i = 0; i < edge; i++){cout<<"\t\t\t";for (int j = 0; j < edge; j++)cout << path[i][j] << "\t";cout << endl;}}DWORD end = timeGetTime()-start;cout<<"\t\t\t使用本方法所用时间为"<<end<<"ms"<<endl;cout<<"\t\t\t按任意键返回菜单！"<<endl;system("pause");menu();
}

（二）算法描述

    算法思想：

    三种方法：第一种为深度优先遍历递归求解，第二种为在深度优先遍历的基础上加入贪心算法求解递归求解，第三种为在深度优先遍历的基础上加入贪心算法求解非递归求解。

    第一种：设置一个递归函数，先判断行动次数是否已经达到64次，若是则递归结束，否则继续进行递归。判断每一次的方向选择是否正确，以是否超出边界还有本个地点是否已经被走过为标准。当符合条件时表示这个方向是正确的，可以进行下一次的递归，否则需要考虑其他方向。

    第二种：第二种方法是建立在第一种方法的基础上的，总体思路与第一种相同，只是在下一步的选择上有了一定的改进，不再是每次都沿着8个方向顺序搜索，而是采用贪心算法选择当前情况下的最优的方向。此处最优的点，在本题中看作后续结点最少的点。进行两次循环，对可行的方向进行累计计算，选取累计结果最小的作为最优点。基于贪心算法可以快速得到搜索结果，效率上有一定的提高。

    第三种：与第二种一个是递归处理，另一个是非递归处理。非递归处理，为了满足这种需求，需要定义一个栈结构，当走到某个位置无法进行下一步时，就将原来栈顶的元素出栈，转而换一条路径继续探索，如果还是无法找到正确的路径，那么就再次出栈，以此类推。如果栈空还未结束，说明没有路径，否则即成功找到路径。

    在求解出马踏棋盘问题后，为使代码更具有普遍性，将棋盘的长宽设置为用户输入，以便于解决其他格式下的问题。为了对这三种方法有更客观的比较，本设计中还设置了对求解时间的显示。

四、完整代码

#include <iostream>
#include <windows.h>
#include<stdio.h>
#include<stdlib.h>
#pragma comment(lib,"winmm.lib")
using namespace std;
#define ROW 8
#define COL 8
#define MAX_STEPS ROW*COL
int move_x[8] = { 1, 2, 2, 1, -1, -2, -2, -1 }; 
int move_y[8] = { 2, 1, -1, -2, -2, -1, 1, 2 };
//深度优先遍历（递归）
void Dfs( int path[8][8], int m, int n, int edge, int count)
{if (count >= edge*edge) return;if (m <= edge-1 && n <= edge-1 && m >= 0 && n >= 0 && path[m][n] == 0){count++; path[m][n] = count; for (int i = 0;i < edge;i++)Dfs(path, m + move_x[i], n + move_y[i], edge, count); return;}elsereturn;
}
//深度优先遍历+贪心算法（递归）
void Dfs_tx(int flag[8][8], int path[8][8], int m, int n, int edge, int count, int found)
{if(found)return;if(count >= edge*edge){found += 1; for(int i = 0; i < edge; i++){for(int j = 0; j < edge; j++)path[i][j] = flag[i][j];}return;}if(m > edge-1 || n > edge-1 || m < 0 || n < 0 || flag[m][n] != 0) return; count++; flag[m][n] = count; int count_next[8] = {-1,-1,-1,-1,-1,-1,-1,-1};for (int i = 0; i < edge; i++){int m_next = m + move_x[i];int n_next = n + move_y[i];     if (m_next < edge && n_next < edge && m_next >= 0 && n_next >= 0 && flag[m_next][n_next] == 0){count_next[i] ++;for (int j = 0; j < edge; j++){int m_next_next = m_next + move_x[j];int n_next_next = n_next + move_y[j];if (m_next_next < edge && n_next_next < edge && m_next_next >= 0 && n_next_next >= 0 && flag[m_next_next][n_next_next] == 0)                count_next[i]++;}}       }int opt_direct = 0;for (int i = 0; i < edge; i++){if (count_next[opt_direct] == -1)opt_direct = i;if ((count_next[i] < count_next[opt_direct]) && count_next[i] != -1){opt_direct = i;}}Dfs_tx( flag, path, m + move_x[opt_direct], n + move_y[opt_direct], edge, count, found); flag[m][n] = 0;                
}
//深度优先遍历+贪心算法（非递归）
typedef struct stack
{int x_adr;      int y_adr;    int direction;
}HORSE_CHESS_STACK;
int chess[ROW+1][COL+1];
int dir[8][2] = {{2,-1},{-2,-1},{-2,1},{2,1},{1,-2},{-1,-2},{-1,2},{1,2}};
int top;
HORSE_CHESS_STACK Adr_Stack[MAX_STEPS];
int out_stack;
void init()
{int n = MAX_STEPS;while(n--){Adr_Stack[n].x_adr = 0;Adr_Stack[n].y_adr = 0;Adr_Stack[n].direction = -1;}Adr_Stack[0].x_adr = 0;Adr_Stack[0].y_adr = 0;Adr_Stack[0].direction = -1;for(int i = 1;i <= ROW;i++){for(int j = 1;j <= COL;j++){chess[ROW][COL] = 0;}}  top = -1;out_stack = 0;
}
void print_stack()
{cout<<"栈中情况:\n";for(int i = 0;i < MAX_STEPS;i++){printf("x:%d  y:%d direction = %d\n",Adr_Stack[i].y_adr,Adr_Stack[i].x_adr,Adr_Stack[i].direction);}cout<<"\n\n";
}
void push_stack(int x_real,int y_real)
{top++;Adr_Stack[top].x_adr = x_real;Adr_Stack[top].y_adr = y_real;Adr_Stack[top].direction = -1; 
}
void pop_stack()
{Adr_Stack[top].x_adr = 0;Adr_Stack[top].y_adr = 0;Adr_Stack[top].direction = -1; top--;
}
void mark_chess(int x,int y)
{chess[y][x] = top + 1;
}
void print_chess_board()
{cout<<"\t\t\troute:"<<endl;for(int i = 1;i <= ROW;i++){cout<<"\t\t\t";for(int j = 1;j <= ROW;j++){printf("%4d ",chess[i][j]);}cout<<endl;}cout<<endl;
}
int t = 1;
void print_steps()
{printf("(%d,%d)",Adr_Stack[top].y_adr,Adr_Stack[top].x_adr);t++;if(t == ROW){cout<<endl;t = 0;}
}
void run_horse_tanxin()
{int x_now,y_now;while(1){if(top >= MAX_STEPS - 1){print_chess_board();break;}x_now = Adr_Stack[top].x_adr;y_now = Adr_Stack[top].y_adr;int next[ROW] = {};for(int i = 0;i < ROW;i++){int x_next = x_now + dir[i][0];int y_next = y_now + dir[i][1];if((x_next > 0 && x_next <= COL) && (y_next > 0 && y_next <= ROW) && chess[y_next][x_next] == 0 ){for(int j = 0;j < ROW;j++){int x_next_next = x_next + dir[j][0];int y_next_next = y_next + dir[j][1];if((x_next_next > 0 && x_next_next <= COL) && (y_next_next > 0 && y_next_next <= ROW) && chess[y_next_next][x_next_next] == 0){next[i]++;}}}}int real_next[8] = {0};int k = 0;int t = ROW + 1;for(int i = 0;i < ROW;i++){t = ROW + 1;for(int j = 0;j < 8;j++){if(next[j] < t){real_next[i] = j;t = next[j];k = j;}}next[k] = ROW + 1;}int dir_now = 0;for(dir_now = Adr_Stack[top].direction + 1;dir_now < ROW;dir_now++){int x_real = x_now + dir[real_next[dir_now]][0];int y_real = y_now + dir[real_next[dir_now]][1];Adr_Stack[top].direction += 1;if((x_real <= COL && x_real > 0) && (y_real <= ROW && y_real > 0) && chess[y_real][x_real] == 0){push_stack(x_real,y_real);mark_chess(x_real,y_real);break;}}if(Adr_Stack[top].direction >= 7){cout<<endl;printf("\n out:(%d,%d) \n",Adr_Stack[top].y_adr,Adr_Stack[top].x_adr);chess[Adr_Stack[top].y_adr][Adr_Stack[top].x_adr] = 0;out_stack++;pop_stack();}//print_stack(); print_steps();}
}
void Dfs_tx_zhan(int m,int n)
{init();push_stack(m,n);mark_chess(m,n);cout<<"\t\t\troute address:\n";printf("(%d,%d)",m,n);run_horse_tanxin();
}
void menu()
{system("cls");cout<<"\t\t\t马踏棋盘问题的解决："<<endl;cout<<"\t\t\t1.深度优先遍历（递归）"<<endl;cout<<"\t\t\t2.深度优先遍历+贪心算法结合（递归）"<<endl;cout<<"\t\t\t3.深度优先遍历+贪心算法结合(非递归）"<<endl;cout<<"\t\t\t0.退出"<<endl;cout<<"\t\t\t请输入选择：";int sel;cin>>sel;if (sel == 0)exit(0);while(sel >3 ||sel <0){cout <<"\t\t\t输入格式错误，请重新输入：";cin>>sel;}int m,n;int found = 0;int edge;cout<<"\t\t\t请输入棋盘的边长：";cin >> edge;cout<<"\t\t\t请输入初始时马的位置：";cin>>m >> n;int flag[8][8]={0};int path[8][8]={0};DWORD start = timeGetTime();if (sel == 1){cout <<"\t\t\t下面是采用深度优先遍历（递归）得出的结果："<<endl;Dfs( path, m, n, edge, 0);}else if (sel == 2){cout <<"\t\t\t下面是采用深度优先遍历+贪心算法结合（递归）得出的结果："<<endl;Dfs_tx( flag, path, m, n, edge, 0, found);}else if (sel == 3){cout<<endl;cout <<"\t\t\t下面是采用深度优先遍历+贪心算法结合（非递归）得出的结果："<<endl;Dfs_tx_zhan(m, n);}if (sel !=3){for (int i = 0; i < edge; i++){cout<<"\t\t\t";for (int j = 0; j < edge; j++)cout << path[i][j] << "\t";cout << endl;}}DWORD end = timeGetTime()-start;cout<<"\t\t\t使用本方法所用时间为"<<end<<"ms"<<endl;cout<<"\t\t\t按任意键返回菜单！"<<endl;system("pause");menu();
}
int main() 
{system("color E0");menu();system("pause");return 0;
}

五、测试与运行

1.菜单

2.第一种方法求解

3.第二种方法求解

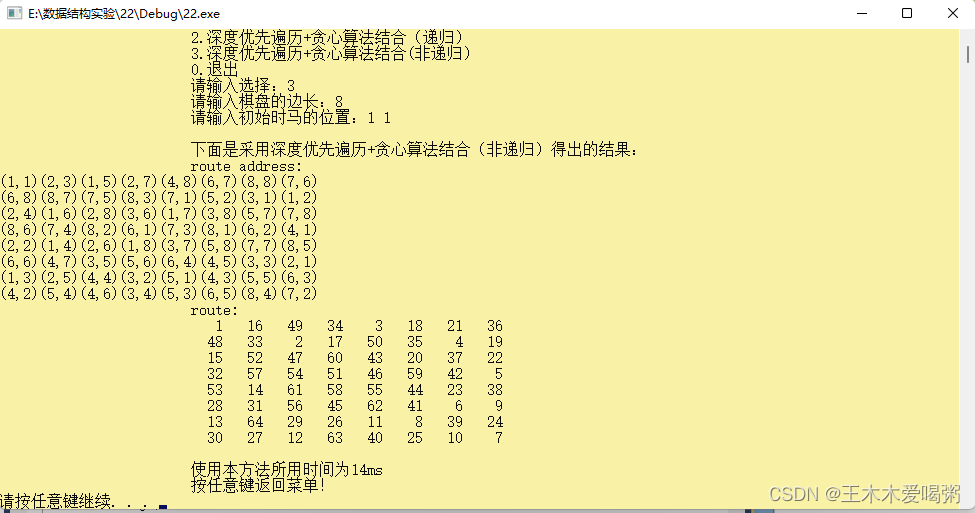
4.第三种方法求解

这篇关于数据结构课程设计---马踏棋盘（C++）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/312057。

相关文章

Java调用C++动态库超详细步骤讲解(附源码)

Java调用C++动态库超详细步骤讲解(附源码)

《Java调用C++动态库超详细步骤讲解(附源码)》C语言因其高效和接近硬件的特性,时常会被用在性能要求较高或者需要直接操作硬件的场合,：本文主要介绍Java调用C++动态库的相关资料,文中通过代... 目录一、直接调用C++库第一步：动态库生成（vs2017+qt5.12.10）第二步：Java调用C++
阅读更多...
C/C++错误信息处理的常见方法及函数

C/C++错误信息处理的常见方法及函数

《C/C++错误信息处理的常见方法及函数》C/C++是两种广泛使用的编程语言,特别是在系统编程、嵌入式开发以及高性能计算领域,：本文主要介绍C/C++错误信息处理的常见方法及函数,文中通过代码介绍... 目录前言1. errno 和 perror()示例：2. strerror()示例：3. perror(
阅读更多...
C++变换迭代器使用方法小结

C++变换迭代器使用方法小结

《C++变换迭代器使用方法小结》本文主要介绍了C++变换迭代器使用方法小结,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧... 目录1、源码2、代码解析代码解析：transform_iterator1. transform_iterat
阅读更多...
详解C++中类的大小决定因数

详解C++中类的大小决定因数

《详解C++中类的大小决定因数》类的大小受多个因素影响,主要包括成员变量、对齐方式、继承关系、虚函数表等,下面就来介绍一下,具有一定的参考价值,感兴趣的可以了解一下... 目录1. 非静态数据成员示例：2. 数据对齐（Padding）示例：3. 虚函数（vtable 指针）示例：4. 继承普通继承虚继承5.
阅读更多...
C++中std::distance使用方法示例

C++中std::distance使用方法示例

《C++中std::distance使用方法示例》std::distance是C++标准库中的一个函数,用于计算两个迭代器之间的距离,本文主要介绍了C++中std::distance使用方法示例,具... 目录语法使用方式解释示例输出：其他说明：总结std::distance&n编程bsp;是 C++ 标准
阅读更多...
C#数据结构之字符串(string)详解

C#数据结构之字符串(string)详解

《C#数据结构之字符串(string)详解》：本文主要介绍C#数据结构之字符串(string),具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录转义字符序列字符串的创建字符串的声明null字符串与空字符串重复单字符字符串的构造字符串的属性和常用方法属性常用方法总结摘
阅读更多...
C++ 中的 if-constexpr语法和作用

C++ 中的 if-constexpr语法和作用

《C++中的if-constexpr语法和作用》if-constexpr语法是C++17引入的新语法特性,也被称为常量if表达式或静态if（staticif）,：本文主要介绍C++中的if-c... 目录1 if-constexpr 语法1.1 基本语法1.2 扩展说明1.2.1 条件表达式1.2.2 fa
阅读更多...
C++中::SHCreateDirectoryEx函数使用方法

C++中::SHCreateDirectoryEx函数使用方法

《C++中::SHCreateDirectoryEx函数使用方法》::SHCreateDirectoryEx用于创建多级目录,类似于mkdir-p命令,本文主要介绍了C++中::SHCreateDir... 目录1. 函数原型与依赖项2. 基本使用示例示例 1：创建单层目录示例 2：创建多级目录3. 关键注
阅读更多...
C++从序列容器中删除元素的四种方法

C++从序列容器中删除元素的四种方法

《C++从序列容器中删除元素的四种方法》删除元素的方法在序列容器和关联容器之间是非常不同的,在序列容器中,vector和string是最常用的,但这里也会介绍deque和list以供全面了解,尽管在一... 目录一、简介二、移除给定位置的元素三、移除与某个值相等的元素3.1、序列容器vector、deque
阅读更多...
C++常见容器获取头元素的方法大全

C++常见容器获取头元素的方法大全

《C++常见容器获取头元素的方法大全》在C++编程中,容器是存储和管理数据集合的重要工具,不同的容器提供了不同的接口来访问和操作其中的元素,获取容器的头元素（即第一个元素）是常见的操作之一,本文将详细... 目录一、std::vector二、std::list三、std::deque四、std::forwa
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2