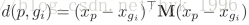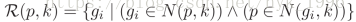Re-ranking Person Re-identification with k-reciprocal Encoding 重排序算法解析

论文：

Re-ranking Person Re-identification with k-reciprocal Encoding

代码：

https://github.com/layumi/Person_reID_baseline_pytorch/blob/master/re_ranking.py

3.提出的方法

3.1 问题定义

给定probe person 和gallery set,可以度量它们的马氏距离：

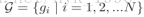
这里和是特征向量，M是半正定矩阵。我们可以根据这个距离对p和G排序，距离从小到大排列：

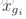
我们的目标是对这个初始排序列表重新排序，使得更多的正样本出现在列表的前段。

3.2 K-reciprocal Nearest Neighbors

首先，定义k-nearest neighbors（k-nn），即排序列表的前k个样本：

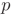
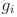
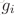
接着，定义k-reciprocal nearest neighbors（k-rnn），简单地说就是满足“和都在对方的k-nn列表里”这一条件的的集合：

然而，由于光照、姿态、视角等一系列变化，正样本可能会被排除到k-nn列表外，因此我们定义了一个更鲁棒的k-rnn集合：

上式的意思是，对于原本的集合R(p,k)中的每一个样本q，找到它们的k-rnn集合R(q,k/2)，对于重合样本数达到一定条件的，则将其并入R(p,k).通过这种方式，将原本不在R(p,k)集合中的正样本重新带回来。文中给了一个例子来说明这一过程，如下图所示：

3.3 Jaccard距离

作者认为，假如两张图片相似，那么它们的k-rnn集合会重叠，即会有重复的样本。重复的样本越多，这两张图片就越相似。那么很自然地就想到用Jaccard Distance度量它们k-rnn集合的相似度：

然而，上面的距离度量有三个缺点：

1.取交集和并集的操作非常耗时间，尤其是在需要计算所有图像对的情况下。一个可选方式是将近邻集编码为一个等价的但是更简单的向量，以减少计算复杂度。

2.这种距离计算方法将所有的近邻样本都认为是同等重要的，而实际上，距离更接近于probe的更可能是正样本。因此，根据原始的距离将大的权值分配给较近的样本这一做法是合理的。

3.单纯考虑上下文信息会在试图测量两个人之间的相似性时造成相当大的障碍。因为，不可避免的变化会使得区分上下文信息变得困难。因此，为了得到鲁棒的距离度量，结合原始距离和Jaccard距离是有必要的。

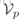
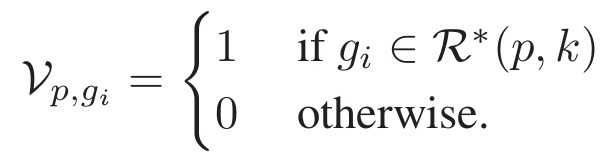
为了克服上述缺点，我们开始改造Jaccard距离。首先，将k-rnn集合编码为N维的二值向量=，其中每个元素由以下指示函数定义：

接着，为了给每一个元素根据原始距离来重新分配权值，我们采用了高斯核。于是将向量改写为：

于是，计算Jaccard距离时用到的交集和并集的基数就改写为：

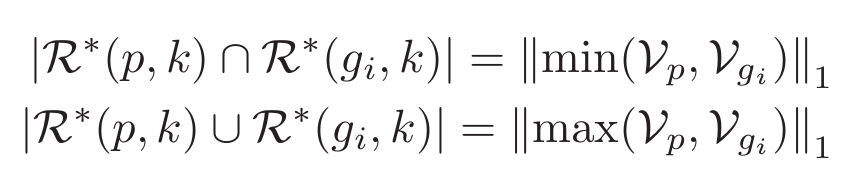
最后，我们终于得到了改造过的Jaccard距离：

这个改造过程，实际上是将集合比较问题转化为纯粹的向量计算，实践起来更简单。

3.4 Local Query Expansion

基于来自同一类的图像可能共享相似特征的想法，我们使用probe的k-nn集合来实现local query expansion，

特别要说明的是，这个query expansion被同时用到了probe 和galleries 上。（这里我的理解是对每个向量定义为其k-nn集合向量的平均，通过这种方法来提升性能。根据我的测试，去掉这一步仍然有不错的效果，但mAP会有少许的下降。）因为k-nn集合可能会混有噪声，因此我们将k值设置得比较小。为了与前面的k做区分，我们定义前面用到的为，而这里用到的为，k1>k2.

3.5 最终距离

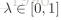
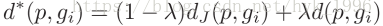
在这里有参数，最终计算距离如下：

3.6 复杂度分析

参考原文内容。

整个重排序的流程图如下所示：