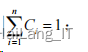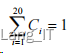本文主要是介绍毕业设计-基于 MATLAB 的课程教学质量评价模型的研究与实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
前言
课题背景和意义
实现技术思路
一、课程教学质量评价模型
二、课程教学质量评价体系设计
部分源代码
实现效果图样例
最后
前言
📅大四是整个大学期间最忙碌的时光,一边要忙着备考或实习为毕业后面临的就业升学做准备,一边要为毕业设计耗费大量精力。近几年各个学校要求的毕设项目越来越难,有不少课题是研究生级别难度的,对本科同学来说是充满挑战。为帮助大家顺利通过和节省时间与精力投入到更重要的就业和考试中去,学长分享优质的选题经验和毕设项目与技术思路。
🚀对毕设有任何疑问都可以问学长哦!
选题指导: https://blog.csdn.net/qq_37340229/article/details/128243277
大家好,这里是海浪学长毕设专题,本次分享的课题是
🎯基于 MATLAB 的课程教学质量评价模型的研究与实现
课题背景和意义
教学质量是教育竞争力的核心内容,是高等教育特别是高职院校的生命线,是教育可持续发展的基础和前提。提高教学质量是各高校特别是高职院校提高教育质量的核心,尤 其是提高教师的课程教学质量。学校教学过程的中心环节是教师课程教学,课程教学是 教师教学质量的集中反映,学校教育质量的高低取决于教师课程教学质量的好坏。所以, 教师课程教学质量评价是教学管理整个评价的一个核心内容,它在整个教师考核过程中占 有举足轻重的作用。 高职学院教学工作是学校常规性的工作,教学质量评价是学校教学管理工作的一项重 要工作,是提高学校办学效益的重要途径,以及保证教学质量的重要手段。为了推进整 个学校教学质量监控保障系统,突出教学工作在整个教学管理工作中的重要地位和核心作 用,同时提高教师的教学质量和教学水平,培养适应国家需求、企业需求和社会需求,具 有实践能力和新时代创新精神,具有德智体美全面发展的优秀人才,学校需要建立一个教 学质量评价对教师的教学质量和其他教学因素进行监控和分析。
实现技术思路
一、课程教学质量评价模型
BP 神经网络基本原理
是通过模拟人脑的功能设计出来的,由大量神经元广泛互连而成的网 络,是对人脑的抽象、简化和模拟,反映了人脑的基本特征 。神经网络具有大规模并行 处理的神经元,具有分布式处理和存储功能,具有自适应、自学习和自组织能力,适合用 于处理一些多条件多因素下不精确模糊的信息处理问题。
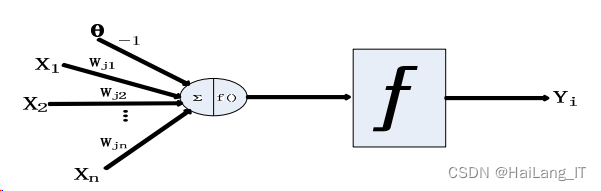
神经元模型
神经元是组成人工神经网络的基本单元,是生物神经元的抽象和模拟,它通常是一个多输入/单输出的非线性元件。一个神经元接收与它相连的所有神经元输出的信息,作为它的输入,使用激励函数计算出相应的输出,再将输出传递给其他的神经元。
BP 神经网络算法原理
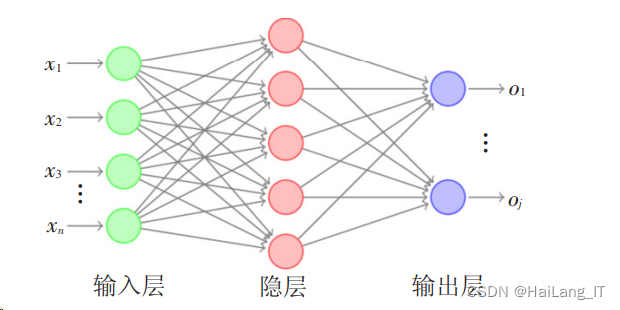
典型的 BP 神经网络由三个部组成,即输入层、隐含层和输出层构成的三层前馈阶层 网络。BP 网络的学习过程是由信号的正向传播和误差的反向传播组成。
如果给定网络一 组输入信息模式时,BP 网络逐步对这组输入信息模式按如下方式进行学习:
1)把输入信息模式从输入层传输到隐含层各单元,经隐含层各单元依次处理后, 产生一个输入信息模式传送到输出层。
2)将网络输出结果值与专家目标值进行分析比较,如果没有达到预计的误差要求, 则转变为误差反向传播(Error Back Propagation)。将误差沿着原路径层返回,通过修正 各层神经元的连接阈值和权值,使误差信号缩小,满足预期要求。
3)这种正向传播和反向传播相互交替计算,看成网络模型“记忆训练”的一个过 程。模型不断地循环这两个过程,重复学习,一直到网络输出值和专家目标值的误差达到 规定的范围内,系统停止学习。如下图所示:
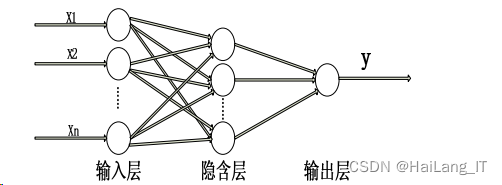
BP 神经网络结构和思路
1、正向传播工作信号
输入层的输入为各个指标的评价数值,即每个指标的评价结果。输入节点 XL=(X1, X2,…,Xp),其中训练样本的序号是 L=1,2,…,n,输入层神经元个数是 p。 隐含层输入量的计算方法 SL=(S1,S2,…,Sm),确定隐含层的神经元个数为 m。加权 和与阈值的差为隐含层输入值,公式如下
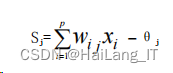
隐含层输出值取 S(Sigmoid)型函数,计算隐含层输出量 BL=(b1,b2,…, bm):
r 为输出层神经元的个数, 计算输出层输入量的方法 CL=(C1,C2,…,Cr)。输出层输 入值为隐含层输出的阈值与加权的差,公式如下:
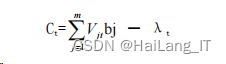
最后,输出层输出值取 S(Sigmoid)函数,输出层输出量计算方法 Yk=(Y1,Y2,…,Yq):
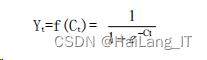
2、反向传播修正误差信号
计算输出层的校正误差,预先设定输出信号 Z L =(Z 1 ,Z 2 ,…,Z p ),公式如下:
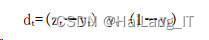
3、训练与收敛
计算第 k 个样本误差公式:
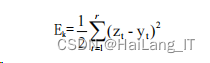
其中 t=1,2,…,r 为输出层单元的序号。本课题的网络输出值为 1,即 r=1,所以第 k 个样本误差公式简化为:
与所有测试样本的平均误差:
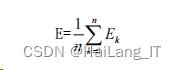
不断对阈值和权值进行修正,经过循环训练多次后,网络的实际输出值与目标期望值达到事先期望的误差,这个过程是整个训练网络误差达到要求的极小值
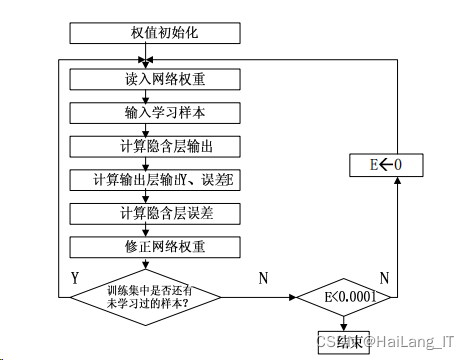
BP 神经网络学习算法
1、最速下降 BP 算法
权值和阈值的修正是在所有样本输入后,计算其总的误差后进行的,这种修正方式称为批处理。
2、拟牛顿算法
牛顿法是一种基于二阶泰勒(Taylor)级数的快速优化算法,其基本方法是
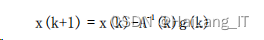
3、LM(levenberg-marquardt)算法
LM 算法与拟牛顿算法一样,是为了在以近似二阶训练速率进行修正时避免计算Hessian 矩阵而设计。

模糊综合评价模型
1、模糊理论
1965 年美国加州大学电气工程师 L.A.Zadeh 教授创立了模糊理论,它的核心是最大限度地模拟人的推理功能和思维。其显著特点是以不确定的因素来代替确定的因素,从而发展更为广阔的领域 。后来,经过科学家的不断研究,使模糊理论加深和提高,成为指导人们实践活动的理论。
2、模糊综合评价原理
综合评价模式是基于加权平均法的思想,故称为“加权平均型”。如果评价因素只有一个层次,可以直接采用单级综合评价模式计算评价结果 。如果评价因素分为多个层次,则需将模式进一步推广到多级模糊综合评价。
模糊综合评价实施步骤
1、构造以下集合:
指标的评价因素集 U={U 1 ,U 2 ,…,U n } ;
评语集 V={V 1 ,V 2 ,…,V m };
评语集对应的数值集 N={n 1 ,n 2 ,…,n m };
权重集 C={c 1 ,c 2 ,…,c n },式 c i 中为第 i 个指标所对应的权重,且
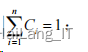
第二步:
构造隶属度子集 R,R i =(r i1 ,r i2 ,…,r im )。这里指评价因素第 i 个指标对应评语集中每个 Vj 的隶属度,即:

第三步:
构建评价矩阵 R。对于每一个评价指标 u i 都可以得到一个隶属度子集 R i ,即构成 U*V 域上的 n*m 的矩阵 R,如下所示:

第五步:

二、课程教学质量评价体系设计
评价的概念及其特征
教学评价是按照一定的教育政策和方针,对照教学要实现的目标,对教学过程中各种教学活动的效果以及发展情况进行系统诊断 ,并提出改进教学方法和提高教学质量有针对性的意见的过程。
在高等教育中,教学评价具有以下 4 点特征:
1)评价方法的科学性2)评价认识的客观性3)评价目的的决策性4)评价内容的综合性
模糊综合评价数据采集
模糊综合评价评语等级集合 V, V={V 1 ,V 2 ,V 3 ,V 4 ,V 5 }, V 1 =优秀;V 2 =良好;V 3 =中等;V 4 =
合格;V 5 =不合格。本课题对教师课程教学质量评价,是从督导专家、同行教师、学生三
方面构成,最后形成一个综合评价结果。
首先建立督导专家模糊评价表,如下表所示:
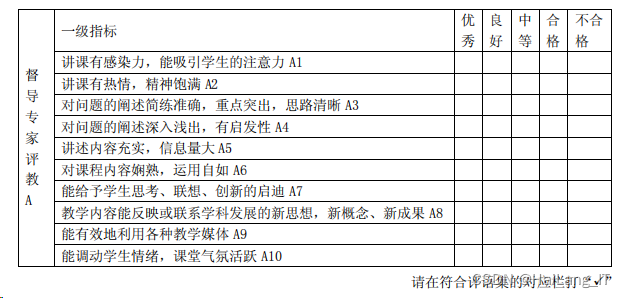
其次建立同行教师模糊评价表,如下表所示:
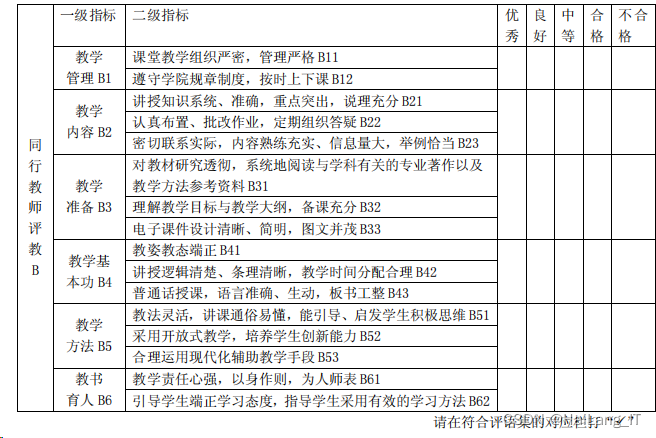
最后建立学生模糊评价表,如下表所示:
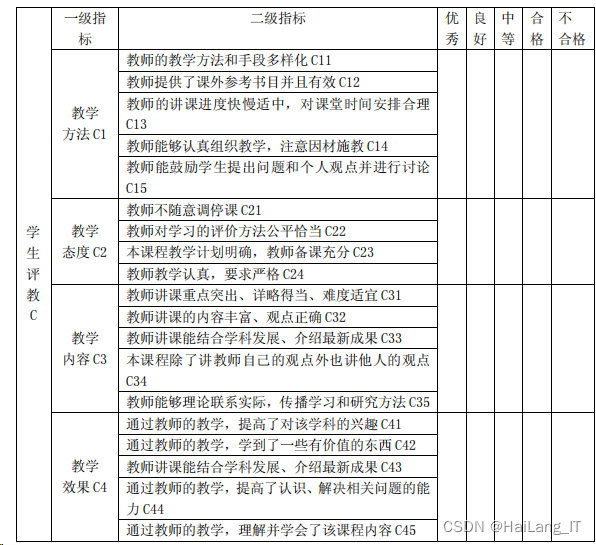
模糊综合评价实验过程
1、实验准备工作
指标因素集 U={U 1 ,U 2 ,…,U 20 },因素有 20 项;评语等级集 V={V 1 ,V 2 ,V 3 ,V 4 ,V 5 }, 评语有 5 项,即优秀、良好、中等、合格、不合格;权重集 C={C1 ,C 2 ,…,C 20},共有 20 项, 式 Ci 中 为 第 i 个 指 标 所 对 应 的 权 重 , 且
评 语 集 对 应 的 数 值 集 N={95,85,75,65,55},构造隶属度子集 R,计算对应 rij,(i=1,2,…,20;j=1,2,3,4,5)即通过公式

建立模糊综合评价定量表,如下表所示:
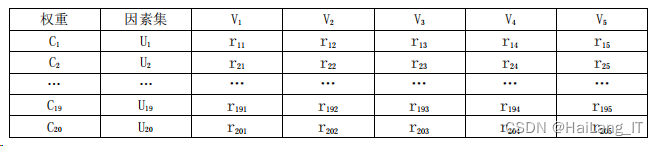
部分源代码
R=[0.6,0.3,0.1,0,0;0.3,0.6,0.1,0,0;0.4,0.4,0.2,0,0;1,0,0,0,0;1,0,0,0,0;0.
8,0.2,0,0,0;0.6,0.4,0,0,0;0.5,0.3,0.2,0,0;0.4,0.4,0.2,0,0;0.5,0.3,0.2,0,0;0.4
,0.4,0.2,0,0;0.8,0.2,0,0,0;0.4,0.4,0.2,0,0;0.5,0.3,0.2,0,0;0.4,0.4,0.2,0,0;0.
4,0.2,0.4,0,0;0.4,0.3,0.3,0,0;0,0.8,0.2,0,0;0.8,0.2,0,0,0;0.8,0.2,0,0,0];
输入权重值:
C=[0.03,0.03,0.03,0.03,0.03,0.03,0.03,0.03,0.03,0.03,0.02,0.03,0.02,0.03,0.03,0.02,0.15,0.1,0.15,0.15];
通过 R1=R(1:20,1)获得矩阵 R 第一列的数值,同理可以得到:
R2=R(1:20,2); %矩阵 R 第二列的数值
R3=R(1:20,3); %矩阵 R 第三列的数值
R4=R(1:20,4); %矩阵 R 第四列的数值
R5=R(1:20,5); %矩阵 R 第五列的数值
通过公式 T1=C*R1 获得 T1 值,同时可以得到:
T2=C*R2
T3=C*R3
T4=C*R4
T5=C*R5
从而获得矩阵 T 的值, T={T1,T2,T3,T4,T5
输出结果代码图

实现效果图样例
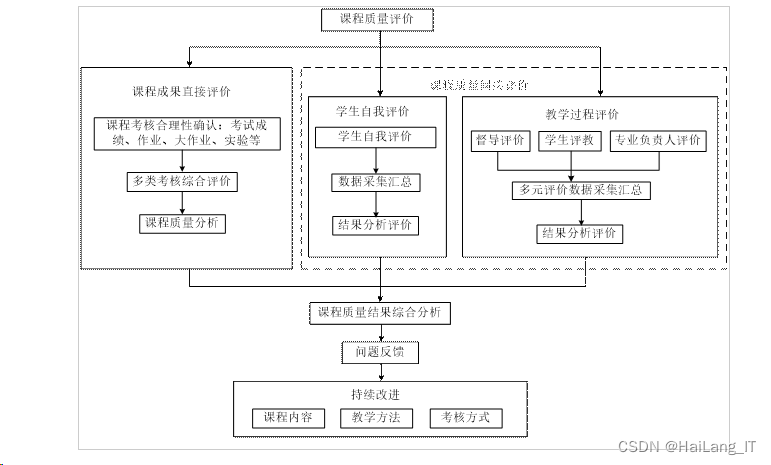
课程质量评价机制图:
我是海浪学长,创作不易,欢迎点赞、关注、收藏、留言。
毕设帮助,疑难解答,欢迎打扰!
最后
这篇关于毕业设计-基于 MATLAB 的课程教学质量评价模型的研究与实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!

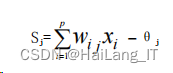
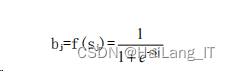
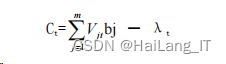
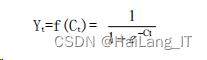
![]()
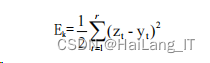
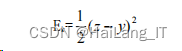
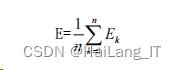

![]()
![]()