本文主要是介绍基于matlab实现的平面波展开法二维声子晶体能带计算程序,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Matlab 平面波展开法计算二维声子晶体二维声子晶体带结构计算,材料是铅柱在橡胶基体中周期排列,格子为正方形。采用PWE方法计算
完整程序:
%%%%%%%%%%%%%%%%%%%%%%%%%
clear;clc;tic;epssys=1.0e-6; %设定一个最小量,避免系统截断误差或除零错误
%%%%%%%%%%%%%%%%%%%%%%%%%%
%定义实际的正空间格子基矢
%%%%%%%%%%%%%%%%%%%%%%%%%%
a=0.02;
a1=a*[1 0];
a2=a*[0 1];
%%%%%%%%%%%%%%%%%%%%%%%%%%
%定义晶格的参数
%%%%%%%%%%%%%%%%%%%%%%%%%%
rho1=11600;E1=4.08e10;mju1=1.49e10;lambda1=mju1*(E1-2*mju1)/(3*mju1-E1); %散射体的材料参数
rho2=1300;E2=1.175e5;mju2=4e4;lambda2=mju2*(E2-2*mju2)/(3*mju2-E2); %基体的材料参数
Rc=0.006; %散射体截面半径
Ac=pi*(Rc)^2; %散射体截面面积
Au=a^2; %二维格子原胞面积
Pf=Ac/Au; %填充率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%生成倒格基矢
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
b1=2*pi/a*[1 0];
b2=2*pi/a*[0 1];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%选定参与运算的倒空间格矢量,即参与运算的平面波数量
%设定一个l,m的取值范围,变化l,m即可得出参与运算的平面波集合
NrSquare=10; %选定倒空间的尺度,即l,m(倒格矢G=l*b1+m*b2)的取值范围。
%NrSquare确定后,使用Bloch波数目可能为(2*NrSquare+1)^2
G=zeros((2*NrSquare+1)^2,2); %初始化可能使用的倒格矢矩阵
i=1;
for l=-NrSquare:NrSquare
for m=-NrSquare:NrSquare
G(i,:)=l*b1+m*b2;
i=i+1;
end;
end;
NG=i-1; %实际使用的Bloch波数目
G=G(1:NG,:);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%生成k空间的rho(Gi-Gj),mju(Gi-Gj),lambda(Gi-Gj)值,i,j从1到NG。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
rho=zeros(NG,NG);mju=zeros(NG,NG);lambda=zeros(NG,NG);
for i=1:NG
for j=1:NG
Gij=norm(G(j,:)-G(i,:));
if (Gij<epssys)
rho(i,j)=rho1*Pf+rho2*(1-Pf);
mju(i,j)=mju1*Pf+mju2*(1-Pf);
lambda(i,j)=lambda1*Pf+lambda2*(1-Pf);
else
rho(i,j)=(rho1-rho2)*2*Pf*besselj(1,Gij*Rc)/(Gij*Rc);
mju(i,j)=(mju1-mju2)*2*Pf*besselj(1,Gij*Rc)/(Gij*Rc);
lambda(i,j)=(lambda1-lambda2)*2*Pf*besselj(1,Gij*Rc)/(Gij*Rc);
end;
end;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%定义简约布里渊区的各高对称点
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
T=(2*pi/a)*[epssys 0];
M=(2*pi/a)*[1/2 1/2];
X=(2*pi/a)*[1/2 0];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对于简约布里渊区边界上的每个k,求解其特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
THETA_A=zeros(NG,NG); %待解的本征方程A矩阵
THETA_B=zeros(NG,NG); %待解的本征方程B矩阵
Nkpoints=10; %每个方向上取的点数
stepsize=0:1/(Nkpoints-1):1; %每个方向上步长
TX_eig=zeros(Nkpoints,NG); %沿TX方向的波的待解的特征频率矩阵
XM_eig=zeros(Nkpoints,NG); %沿XM方向的波的待解的特征频率矩阵
MT_eig=zeros(Nkpoints,NG); %沿MT方向的波的待解的特征频率矩阵
for n=1:Nkpoints
fprintf(['\n k-point:',int2str(n),'of',int2str(Nkpoints),'.\n']);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对于TX(正方格子)方向上的每个k值,求解其特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
TX_step=stepsize(n)*(X-T)+T;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%n 求本征矩阵的元素
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:NG
for j=1:NG
kGi=TX_step+G(i,:);
kGj=TX_step+G(j,:);
THETA_A(i,j)=mju(i,j)*dot(kGi,kGj);
THETA_B(i,j)=rho(i,j);
end;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求解TX(正方格子)方向上的k矩阵的特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
TX_eig(n,:)=sort(sqrt(eig(THETA_A,THETA_B))).';
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对于XM(正方格子)方向上的每个k值,求解其特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
XM_step=stepsize(n)*(M-X)+X;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%n 求本征矩阵的元素
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:NG
for j=1:NG
kGi=XM_step+G(i,:);
kGj=XM_step+G(j,:);
THETA_A(i,j)=mju(i,j)*dot(kGi,kGj);
THETA_B(i,j)=rho(i,j);
end;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求解XM(正方格子)方向上的k矩阵的特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
XM_eig(n,:)=sort(sqrt(eig(THETA_A,THETA_B))).';
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对于MT(正方格子)方向上的每个k值,求解其特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
MT_step=stepsize(n)*(T-M)+M;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%n 求本征矩阵的元素
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:NG
for j=1:NG
kGi=MT_step+G(i,:);
kGj=MT_step+G(j,:);
THETA_A(i,j)=mju(i,j)*dot(kGi,kGj);
THETA_B(i,j)=rho(i,j);
end;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求解MT(正方格子)方向上的k矩阵的特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
MT_eig(n,:)=sort(sqrt(eig(THETA_A,THETA_B))).';
end;
fprintf('\n Calculation Time:%d sec',toc);
save pbs2D
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%绘制声子晶体能带结构图
%首先将特定方向(正方格子:TX,XM,MT)离散化
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
kaxis=0;
TXaxis=kaxis:norm(T-X)/(Nkpoints-1):(kaxis+norm(T-X));
kaxis=kaxis+norm(T-X);
XMaxis=kaxis:norm(M-X)/(Nkpoints-1):(kaxis+norm(X-M));
kaxis=kaxis+norm(X-M);
MTaxis=kaxis:norm(T-M)/(Nkpoints-1):(kaxis+norm(T-M));
kaxis=kaxis+norm(T-M);
Ntraject=3; %所需绘制的特定方向的数目
EigFreq=zeros(Ntraject*Nkpoints,1);
figure(1)
hold on;
Nk=Nkpoints;
for k=1:NG
for i=1:Nkpoints
EigFreq(i+0*Nk)=TX_eig(i,k)/(2*pi);
EigFreq(i+1*Nk)=XM_eig(i,k)/(2*pi);
EigFreq(i+2*Nk)=MT_eig(i,k)/(2*pi);
end;
plot(TXaxis(1:Nk),EigFreq(1+0*Nk:1*Nk),'b',...
XMaxis(1:Nk),EigFreq(1+1*Nk:2*Nk),'b',...
MTaxis(1:Nk),EigFreq(1+2*Nk:3*Nk),'b');
end;
grid on;
hold off;
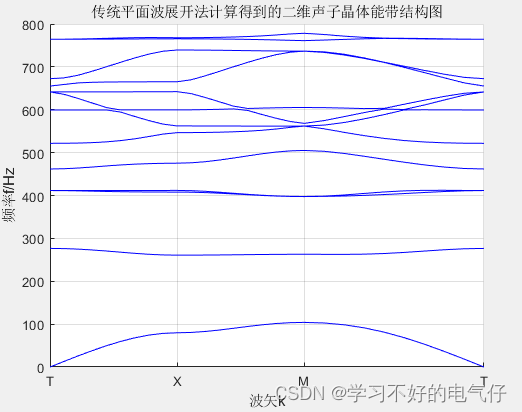
titlestr='传统平面波展开法计算得到的二维声子晶体能带结构图';
title(titlestr);
xlabel('波矢k');
ylabel('频率f/Hz');
axis([0 MTaxis(Nkpoints) 0 800]);
set(gca,'XTick',[TXaxis(1) TXaxis(Nkpoints) XMaxis(Nkpoints) MTaxis(Nkpoints)]);
xtixlabel=char('T','X','M','T');
set(gca,'XTickLabel',xtixlabel);
这篇关于基于matlab实现的平面波展开法二维声子晶体能带计算程序的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




