数据结构上机实验——二叉树的实现、二叉树遍历、求二叉树的深度/节点数目/叶节点数目、计算二叉树度为1或2的节点数、判断二叉树是否相似

2023-10-29 17:36
文章标签 二叉树 遍历 实现 计算 数据结构 深度 判断 是否 实验 节点 上机 数目 相似 度为

本文主要是介绍数据结构上机实验——二叉树的实现、二叉树遍历、求二叉树的深度/节点数目/叶节点数目、计算二叉树度为1或2的节点数、判断二叉树是否相似，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

  • 数据结构上机实验
    • 1.要求
    • 2.二叉树的实现
      • 2.1创建一颗二叉树
      • 2.2对这棵二叉树进行遍历
      • 2.3求二叉树的深度/节点数目/叶节点数目
      • 2.4计算二叉树中度为 1 或 2 的结点数
      • 2.5判断2棵二叉树是否相似，若相似返回1，否则返回0
    • 3.全部源码
      • 测试：
      • BinaryTree.h
      • test.cpp

数据结构上机实验

1.要求

   建立一棵二叉树，试编程实现二叉树的如下基本操作。
   1.创建一棵一棵二叉算法。
   2.对这棵二叉树进行遍历：先序或中序或后序，分别输出结点的遍历序列。
   3.求二叉树的深度/节点数目/叶节点数目。（选做一个）
   4.计算二叉树中度为1 的结点数；
   5.计算二叉树中度为2 的结点数。
   6.判断2棵二叉树是否相似，若相似返回1，否则返回0

            

2.二叉树的实现

  二叉树的介绍
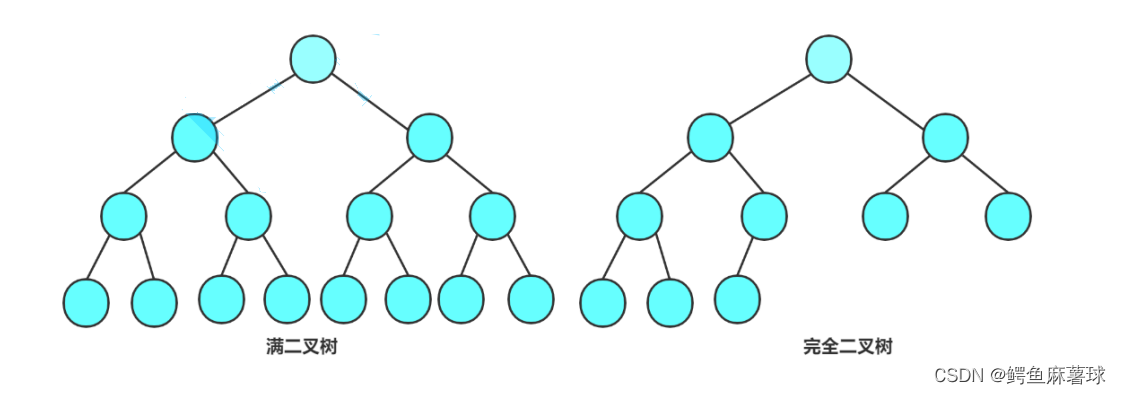
在这里插入图片描述
  

2.1创建一颗二叉树

  我们现在可以简单实现一个二叉树的结构，其中包括一个二叉树节点（BNode）和一个二叉树（BTree）类。

  我们定义了一个名为BNode的结构体，它代表二叉树的节点。每个节点包含一个数据元素（data，其类型为int）和两个指向其左右子节点的指针（left和right）。

  然后定义了一个名为BTree的类，它包含一个私有成员变量_root，这是一个指向BNode的指针。这个指针表示了树的根节点。这个类还包含一个默认的构造函数，该构造函数将_root初始化为nullptr，即没有初始的根节点。

#define BTDataType int//定义二叉树节点
typedef struct BTreeNode
{BTDataType data;struct BTreeNode* left;struct BTreeNode* right;
}BNode;//定义二叉树
class BTree
{
public://构造函数BTree(){_root = nullptr;}private:BNode* _root;
};

  
输入字符递归创建二叉树：
  我们先使用引用接受一个 BNode*类型的参数 root。这样我们就可以在函数内部，直接对 root 进行操作，最后返回给tmp，再赋给_root。

  这个函数首先从标准输入读取一个字符 val。如果 val 是 . ，则 root 被设置为 nullptr，表示该节点为空。如果 val 不是 .，则创建一个新的 BNode 对象，其 data 成员的值为 val 减去字符 ‘0’ 的 ASCII 值（这样可以获得一个整数），然后递归地创建这个新节点的左子树和右子树。最后，_BTCreate 返回，控制权回到调用该函数的代码。

//递归创建二叉树
void _BTCreate(BNode*& root)
{char val;cin >> val;if (val == '.') root = nullptr;else{root = new BNode(val - '0');_BTCreate(root->left);_BTCreate(root->right);}
}//递归创建二叉树
void BTCreate()
{BNode* tmp;_BTCreate(tmp);_root = tmp;
}

  

2.2对这棵二叉树进行遍历

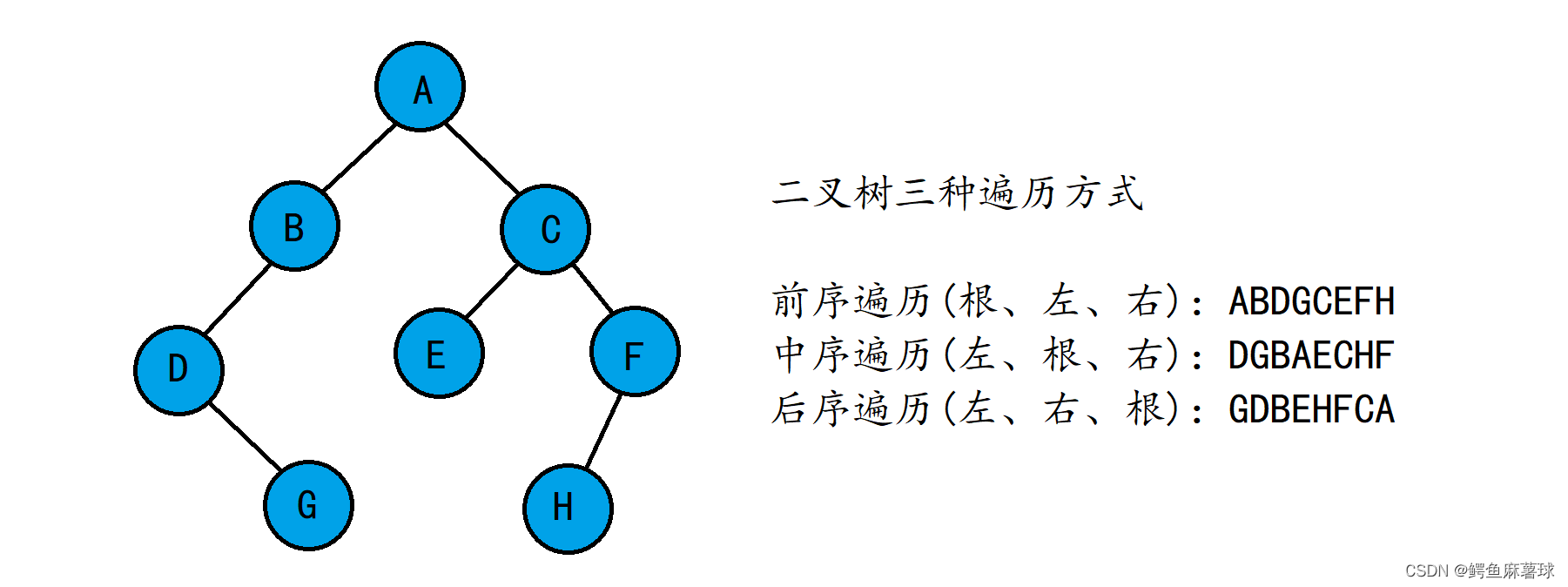
在这里插入图片描述

前序遍历：

  我们创建_PreOrder(BNode* root)这个函数是用来前序遍历。它的顺序是：先访问根节点，然后访问左子树，最后访问右子树。

  如果 root 是 nullptr（即当前节点为空），它将输出 “NULL” 并返回。如果 root 非空，它会输出当前节点的数据（root->data），然后递归地对左子树和右子树进行前序遍历。

  由于二叉树的前序遍历是一个递归算法，为了可以将根节点不断的更新，并且递归。 我们需要封装一下，对于后面需要递归的函数，我们都需要将根节点作为参数，进行递归操作。

//前序遍历
void _PreOrder(BNode* root)
{if (root == nullptr){cout << "NULL" << " ";return;}cout << root->data << " ";_PreOrder(root->left);_PreOrder(root->right);
}//前序遍历
void PreOrder()
{_PreOrder(_root);cout << endl;
}

  
中序遍历：

  我们创建 _InOrder(BNode* root) 来进行中序遍历，它的顺序是：先访问左子树，然后访问根节点，最后访问右子树。

  如果 root 是 nullptr，表示当前节点为空，输出 “NULL” 并返回。如果 root 非空，先递归地遍历左子树，然后输出当前节点的数据 root->data，最后递归地遍历右子树。

//中序遍历
void _InOrder(BNode* root)
{if (root == nullptr){cout << "NULL" << " ";return;}_InOrder(root->left);cout << root->data << " ";_InOrder(root->right);
}//中序遍历
void InOrder()
{_InOrder(_root);cout << endl;
}

  
后序遍历：

  我们创建 _PostOrder(BNode* root) 函数来进行进行后序遍历，它的顺序是：先访问左子树，然后访问右子树，最后访问根节点。

  如果 root 是 nullptr，表示当前节点为空，输出 “NULL” 并返回。如果 root 非空，先递归地遍历左子树，然后递归地遍历右子树，最后输出当前节点的数据 root->data。

//后序遍历
void _PostOrder(BNode* root)
{if (root == nullptr){cout << "NULL" << " ";return;}_PostOrder(root->left);_PostOrder(root->right);cout << root->data << " ";
}//后序遍历
void PostOrder()
{_PostOrder(_root);cout<<endl;
}

  

2.3求二叉树的深度/节点数目/叶节点数目

计算二叉树深度：

  我们使用递归的方式来实现计算二叉树的深度。二叉树的深度可以定义为左子树和右子树深度的最大值加1。

  函数接受的参数root 是 NULL，即当前节点为空，那么返回深度为0。否则，递归地计算左子树和右子树的深度，并返回其中较大的一个，并加上1（当前节点的深度）。

//计算二叉树深度
int _BTDepth(BNode* root)
{if (root == NULL){return 0;}else{int left_Height = _BTDepth(root->left) + 1;int right_Height = _BTDepth(root->right) + 1;if (left_Height >= right_Height) return left_Height;else return right_Height;}
}//计算二叉树深度
int	BTDepth()
{return _BTDepth(_root);
}

  
计算二叉树节点数目：

  我们递归实现_Num_Of_TreeNode来计算二叉树的节点数目。

  首先我们接收一个指向二叉树节点的指针 root 作为参数。如果 root 是 NULL（也就是说，当前节点不存在），函数返回0。否则，则说明该二叉树的节点存在，函数返回1（对于当前节点） 加上左子树和右子树的节点数目。这是通过递归调用 _Num_Of_TreeNode 函数得到的。

//计算二叉树节点数目
int _Num_Of_TreeNode(BNode* root)
{if (root == NULL){return 0;}else{return 1 + _Num_Of_TreeNode(root->left) + _Num_Of_TreeNode(root->right);}
}//计算二叉树节点数目
int Num_Of_TreeNode()
{return _Num_Of_TreeNode(_root);
}

  
计算二叉树叶子节点的数目:

  我们同样创建递归函数 _Num_Of_LeafNode来计算二叉树的叶子节点。

  我们接收一个指向二叉树节点的指针 root 作为参数。如果 root 是 NULL（也就是说，当前节点不存在），函数返回0。否则，函数首先递归地计算左子树和右子树的叶子节点数量，分别存储在 left_Num 和 right_Num 中。

  注意：如果 left_Num 和 right_Num 的和为0，这意味着当前节点是叶子节点，因此返回1。 如果 left_Num 和 right_Num 的和不为0，这意味着当前节点不是叶子节点，因此返回 left_Num 和 right_Num 的和。

//计算二叉树叶子节点的数目
int _Num_Of_LeafNode(BNode* root)
{if (root == NULL){return 0;}else{int left_Num = _Num_Of_LeafNode(root->left);int right_Num = _Num_Of_LeafNode(root->right);if (left_Num + right_Num == 0){return 1;}else{return left_Num + right_Num;}}
}//计算二叉树叶子节点的数目
int Num_Of_LeafNode()
{return _Num_Of_LeafNode(_root);
}

  

2.4计算二叉树中度为 1 或 2 的结点数

  
计算度为1的节点个数：

  二叉树的递归函数大差不差，我们对于求不同的节点，只要加以它们的性质判断即可。

  如果二叉树的节点度为2，说明它们均有左右节点。 所以，此时函数返回的是左子树和右子树中1度节点的总和。

  只有右节点: 如果一个节点只有右子节点，那么它是1度节点。 因此，这个分支计算了右子树中的1度节点数量，并加上1（表示当前节点）。

  只有左节点: 与上述逻辑类似，如果一个节点只有左子节点， 那么它也是1度节点。这个分支计算了左子树中的1度节点数量，并加上1（表示当前节点）。

  无左右节点: 如果一个节点既没有左子节点也没有右子节点，那么它不是1度节点。函数返回0。

//计算度为1的节点个数
int _Num_Of_Degree_1(BNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right != NULL || root->left != NULL && root->right == NULL){return 1 + _Num_Of_Degree_1(root->left) + _Num_Of_Degree_1(root->right);}return  _Num_Of_Degree_1(root->left) + _Num_Of_Degree_1(root->right);
}//计算二叉树节点数目
int Num_Of_TreeNode()
{return _Num_Of_TreeNode(_root);
}

  
计算度为2的节点个数：

  和上面一样，我们实现计算一个二叉树中度为2的节点的数量。度为2的节点是指有两个子节点的节点。

  如果 root 的左右子节点都不为空(root->left != NULL and root->right != NULL)，则说明当前节点的度为2，返回1（对于当前节点）加上左子树和右子树的度为1的节点数量之和。

  只有右子节点不为空，则只返回右子树的度为1的节点数量。

  只有左子节点不为空，则只返回左子树的度为1的节点数量。

  左右子节点都为空，则当前节点不是度为2的节点，返回0。

//计算度为2的节点个数
int _Num_Of_Degree_2(BNode* root)
{if (root == NULL){return 0;}else if(root->left != NULL && root->right != NULL)//均有左右节点{return 1 + _Num_Of_Degree_2(root->left) + _Num_Of_Degree_2(root->right);}return _Num_Of_Degree_2(root->right)+ _Num_Of_Degree_2(root->left);
}//计算度为2的节点个数
int Num_Of_Degree_2()
{return _Num_Of_Degree_2(_root);
}

  

2.5判断2棵二叉树是否相似，若相似返回1，否则返回0

  这个函数是用来判断两棵二叉树是否相似的。相似二叉树的定义是：如果两棵二叉树的结构相同，即它们的左子树和右子树都是相似的，那么这两棵二叉树就是相似的。

  这个函数使用递归的方式进行检查。首先，如果两个节点都为空，那么它们显然是相似的。然后，如果两个节点都不为空，并且它们的左子树和右子树都是相似的，那么这两个节点也是相似的。 最后，如果以上条件都不满足，那么这两个节点就不相似。

//判断二叉树是否相似
int Is_Similar(BNode* t1, BNode* t2)
{if (t1 == NULL && t2 == NULL){return 1;}else if (t1 && t2 && Is_Similar(t1->left, t2->left)&& Is_Similar(t1->right, t2->right)){return 1;}else{return 0;}
}

            

3.全部源码

测试：

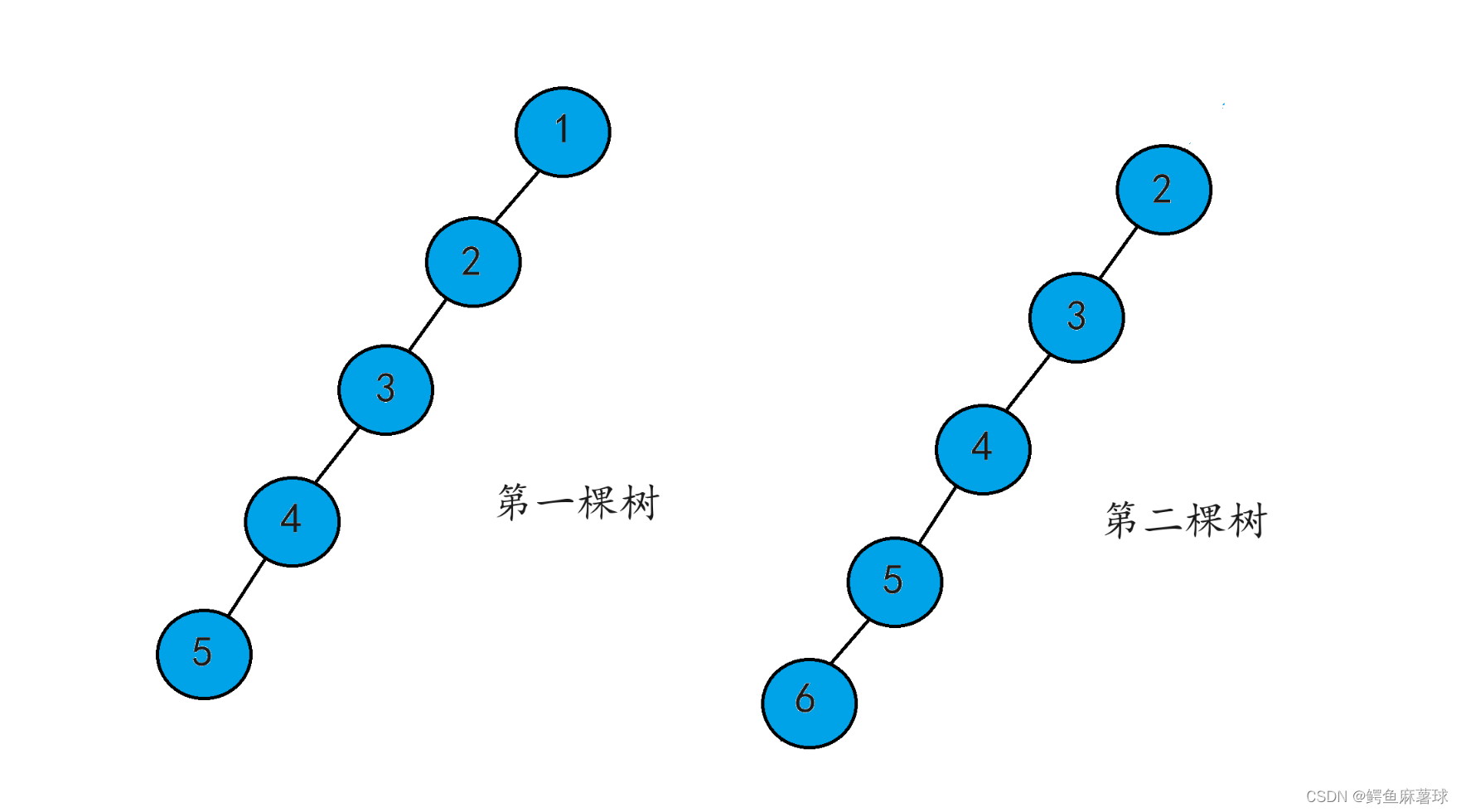
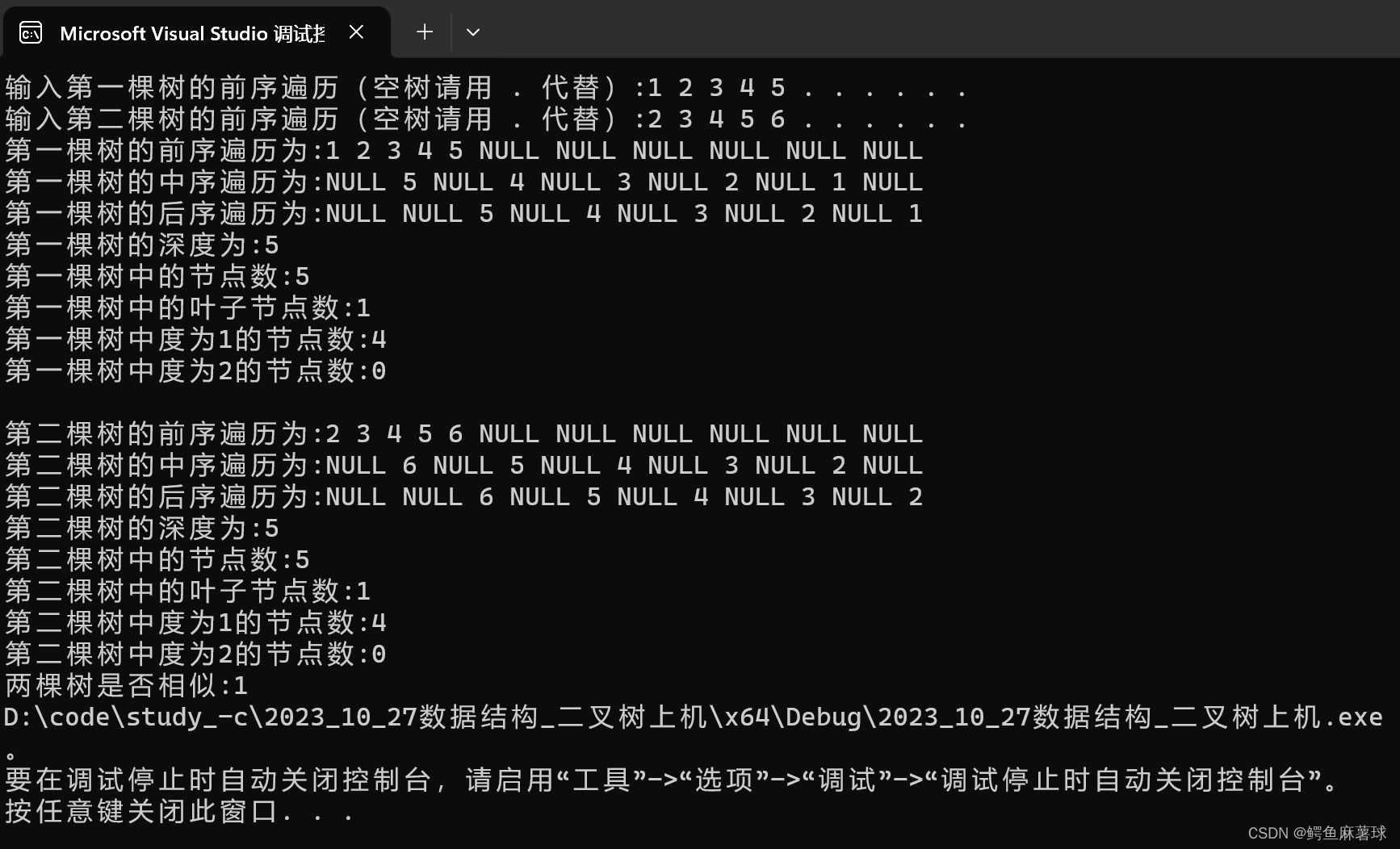
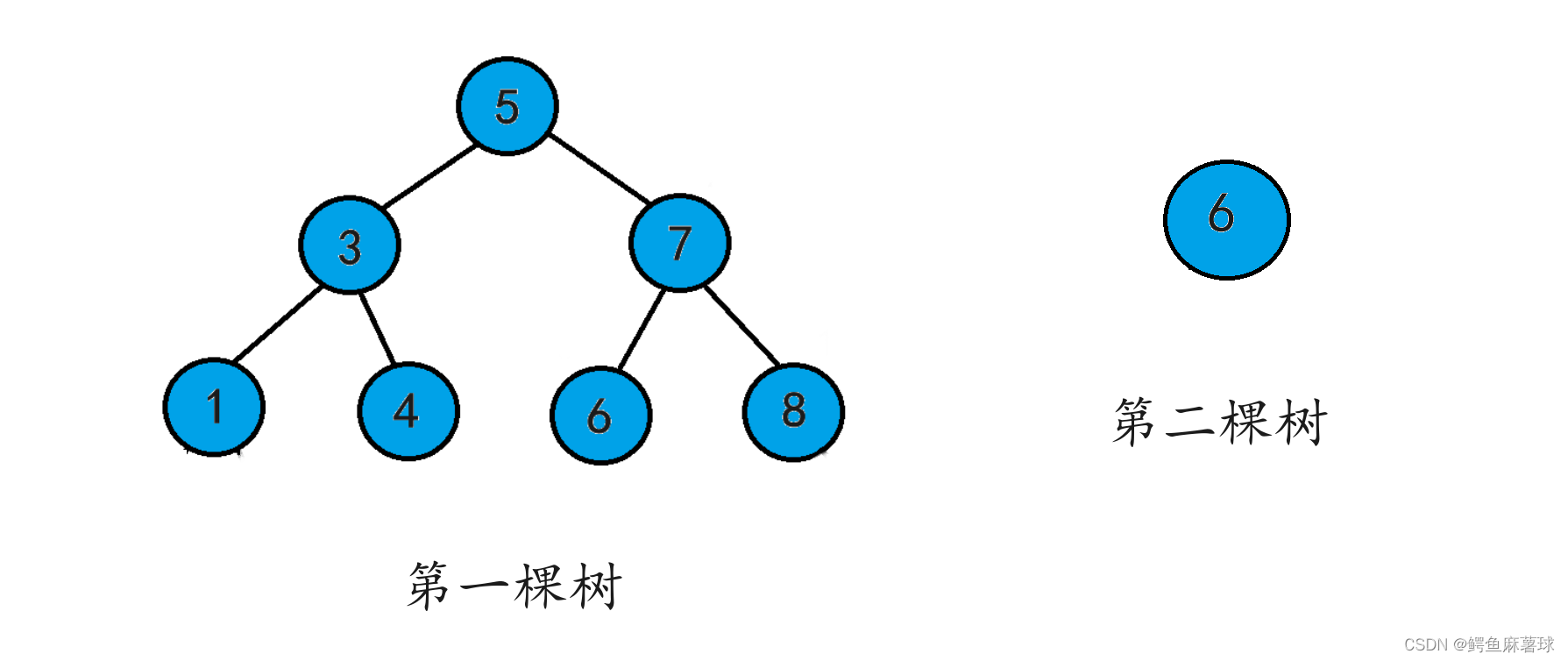
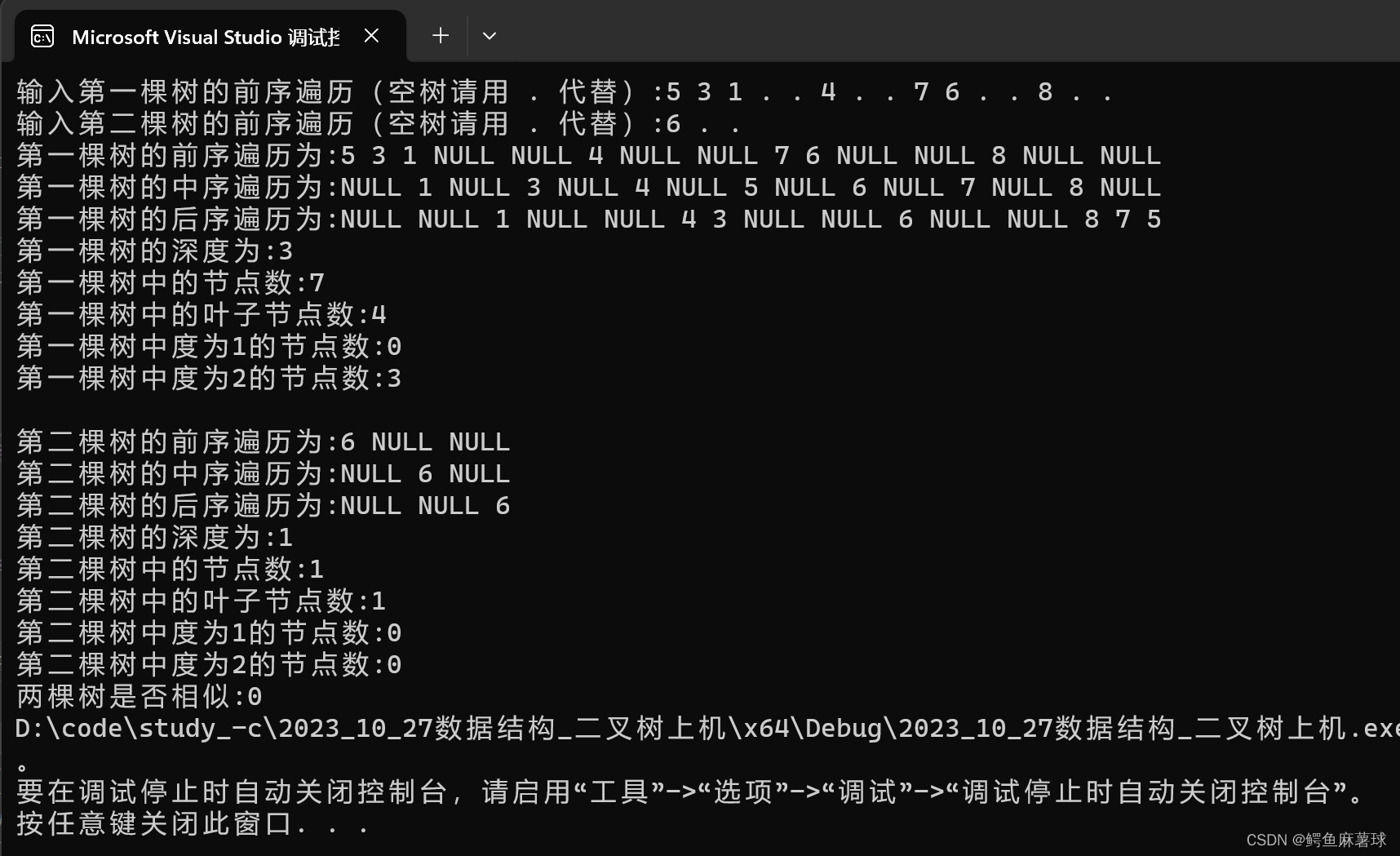
在这里插入图片描述
在这里插入图片描述
  

在这里插入图片描述
在这里插入图片描述

BinaryTree.h

#pragma once#define BTDataType int//定义二叉树节点
typedef struct BTreeNode
{BTDataType data;struct BTreeNode* left;struct BTreeNode* right;BTreeNode() {data = -1;left = nullptr;right = nullptr;}BTreeNode(const int& _data){data = _data;left = nullptr;right = nullptr;}
}BNode;//定义二叉树
class BTree
{
public://构造函数BTree(){_root = nullptr;}//析构函数~BTree(){DestroyTree(_root);}//递归创建二叉树void BTCreate(){BNode* tmp;_BTCreate(tmp);_root = tmp;}//前序遍历void PreOrder(){_PreOrder(_root);cout << endl;}//中序遍历void InOrder(){_InOrder(_root);cout << endl;}//后序遍历void PostOrder(){_PostOrder(_root);cout<<endl;}//计算二叉树深度int	BTDepth(){return _BTDepth(_root);}//计算二叉树节点数目int Num_Of_TreeNode(){return _Num_Of_TreeNode(_root);}//计算二叉树叶子节点的数目int Num_Of_LeafNode(){return _Num_Of_LeafNode(_root);}//计算度为1的节点个数int Num_Of_Degree_1(){return _Num_Of_Degree_1(_root);}//计算度为2的节点个数int Num_Of_Degree_2(){return _Num_Of_Degree_2(_root);}//判断二叉树是否相似int Is_Similar(BNode* t1, BNode* t2){if (t1 == NULL && t2 == NULL){return 1;}else if (t1 && t2 && Is_Similar(t1->left, t2->left) && Is_Similar(t1->right, t2->right)){return 1;}else{return 0;}}//取根节点BNode*& GetRoot(){return _root;}private://递归创建二叉树void _BTCreate(BNode*& root){char val;cin >> val;if (val == '.') root = nullptr;else{root = new BNode(val - '0');_BTCreate(root->left);_BTCreate(root->right);}}//前序遍历void _PreOrder(BNode* root){if (root == nullptr){cout << "NULL" << " ";return;}cout << root->data << " ";_PreOrder(root->left);_PreOrder(root->right);}//中序遍历void _InOrder(BNode* root){if (root == nullptr){cout << "NULL" << " ";return;}_InOrder(root->left);cout << root->data << " ";_InOrder(root->right);}//后序遍历void _PostOrder(BNode* root){if (root == nullptr){cout << "NULL" << " ";return;}_PostOrder(root->left);_PostOrder(root->right);cout << root->data << " ";}//计算二叉树深度int _BTDepth(BNode* root){if (root == NULL){return 0;}else{int left_Height = _BTDepth(root->left) + 1;int right_Height = _BTDepth(root->right) + 1;if (left_Height >= right_Height) return left_Height;else return right_Height;}}//计算二叉树节点数目int _Num_Of_TreeNode(BNode* root){if (root == NULL){return 0;}else{return 1 + _Num_Of_TreeNode(root->left) + _Num_Of_TreeNode(root->right);}}//计算二叉树叶子节点的数目int _Num_Of_LeafNode(BNode* root){if (root == NULL){return 0;}else{int left_Num = _Num_Of_LeafNode(root->left);int right_Num = _Num_Of_LeafNode(root->right);if (left_Num + right_Num == 0){return 1;}else{return left_Num + right_Num;}}}//计算度为1的节点个数int _Num_Of_Degree_1(BNode* root){if (root == NULL){return 0;}if (root->left == NULL && root->right != NULL || root->left != NULL && root->right == NULL){return 1 + _Num_Of_Degree_1(root->left) + _Num_Of_Degree_1(root->right);}return  _Num_Of_Degree_1(root->left) + _Num_Of_Degree_1(root->right);}//计算度为2的节点个数int _Num_Of_Degree_2(BNode* root){if (root == NULL){return 0;}else if(root->left != NULL && root->right != NULL)//均有左右节点{return 1 + _Num_Of_Degree_2(root->left) + _Num_Of_Degree_2(root->right);}return  _Num_Of_Degree_2(root->left) + _Num_Of_Degree_2(root->right);}//销毁二叉树void DestroyTree(BNode*& root) {if (root == NULL) {return;}BNode* lroot = root->left;BNode* rroot = root->right;delete root;if (lroot != NULL){DestroyTree(lroot);}if (rroot != NULL){DestroyTree(rroot);}}private:BNode* _root;
};

            

test.cpp

#define _CRT_SECURE_NO_WARNINGS 1#include<iostream>
using namespace std;#include"BinaryTree.h" void binary_Test()
{BTree bt1;BTree bt2;cout << "输入第一棵树的前序遍历（空树请用 . 代替）:";bt1.BTCreate();cout << "输入第二棵树的前序遍历（空树请用 . 代替）:";bt2.BTCreate(); cout << "第一棵树的前序遍历为:";bt1.PreOrder();cout << "第一棵树的中序遍历为:"; bt1.InOrder();	cout << "第一棵树的后序遍历为:"; bt1.PostOrder();cout << "第一棵树的深度为:" << bt1.BTDepth() << endl;cout << "第一棵树中的节点数:" << bt1.Num_Of_TreeNode() << endl;cout << "第一棵树中的叶子节点数:" << bt1.Num_Of_LeafNode() << endl;cout << "第一棵树中度为1的节点数:" << bt1.Num_Of_Degree_1() << endl;cout << "第一棵树中度为2的节点数:" << bt1.Num_Of_Degree_2() << endl;cout << endl;cout << "第二棵树的前序遍历为:";bt2.PreOrder();cout << "第二棵树的中序遍历为:";bt2.InOrder();cout << "第二棵树的后序遍历为:";bt2.PostOrder();cout << "第二棵树的深度为:" << bt2.BTDepth() << endl;cout << "第二棵树中的节点数:" << bt2.Num_Of_TreeNode() << endl;cout << "第二棵树中的叶子节点数:" << bt2.Num_Of_LeafNode() << endl;cout << "第二棵树中度为1的节点数:" << bt2.Num_Of_Degree_1() << endl;cout << "第二棵树中度为2的节点数:" << bt2.Num_Of_Degree_2() << endl;cout << "两棵树是否相似:" << bt1.Is_Similar(bt1.GetRoot(), bt2.GetRoot());
}int main()
{binary_Test();return 0;
}

这篇关于数据结构上机实验——二叉树的实现、二叉树遍历、求二叉树的深度/节点数目/叶节点数目、计算二叉树度为1或2的节点数、判断二叉树是否相似的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/302242。

相关文章

windows和Linux使用命令行计算文件的MD5值

windows和Linux使用命令行计算文件的MD5值

《windows和Linux使用命令行计算文件的MD5值》在Windows和Linux系统中,您可以使用命令行（终端或命令提示符）来计算文件的MD5值,文章介绍了在Windows和Linux/macO... 目录在Windows上：在linux或MACOS上：总结在Windows上：可以使用certuti
阅读更多...
使用Python实现IP地址和端口状态检测与监控

使用Python实现IP地址和端口状态检测与监控

《使用Python实现IP地址和端口状态检测与监控》在网络运维和服务器管理中,IP地址和端口的可用性监控是保障业务连续性的基础需求,本文将带你用Python从零打造一个高可用IP监控系统,感兴趣的小伙... 目录概述：为什么需要IP监控系统使用步骤说明1. 环境准备2. 系统部署3. 核心功能配置系统效果展
阅读更多...
Python实现微信自动锁定工具

Python实现微信自动锁定工具

《Python实现微信自动锁定工具》在数字化办公时代,微信已成为职场沟通的重要工具,但临时离开时忘记锁屏可能导致敏感信息泄露,下面我们就来看看如何使用Python打造一个微信自动锁定工具吧... 目录引言：当微信隐私遇到自动化守护效果展示核心功能全景图技术亮点深度解析1. 无操作检测引擎2. 微信路径智能获
阅读更多...
Python中pywin32 常用窗口操作的实现

Python中pywin32 常用窗口操作的实现

《Python中pywin32常用窗口操作的实现》本文主要介绍了Python中pywin32常用窗口操作的实现,pywin32主要的作用是供Python开发者快速调用WindowsAPI的一个... 目录获取窗口句柄获取最前端窗口句柄获取指定坐标处的窗口根据窗口的完整标题匹配获取句柄根据窗口的类别匹配获取句
阅读更多...
在 Spring Boot 中实现异常处理最佳实践

在 Spring Boot 中实现异常处理最佳实践

《在SpringBoot中实现异常处理最佳实践》本文介绍如何在SpringBoot中实现异常处理,涵盖核心概念、实现方法、与先前查询的集成、性能分析、常见问题和最佳实践,感兴趣的朋友一起看看吧... 目录一、Spring Boot 异常处理的背景与核心概念1.1 为什么需要异常处理？1.2 Spring B
阅读更多...
判断PyTorch是GPU版还是CPU版的方法小结

判断PyTorch是GPU版还是CPU版的方法小结

《判断PyTorch是GPU版还是CPU版的方法小结》PyTorch作为当前最流行的深度学习框架之一,支持在CPU和GPU(NVIDIACUDA)上运行,所以对于深度学习开发者来说,正确识别PyTor... 目录前言为什么需要区分GPU和CPU版本？性能差异硬件要求如何检查PyTorch版本？方法1：使用命
阅读更多...
Python位移操作和位运算的实现示例

Python位移操作和位运算的实现示例

《Python位移操作和位运算的实现示例》本文主要介绍了Python位移操作和位运算的实现示例,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一... 目录1. 位移操作1.1 左移操作 (<<)1.2 右移操作 (>>)注意事项：2. 位运算2.1
阅读更多...
如何在 Spring Boot 中实现 FreeMarker 模板

如何在 Spring Boot 中实现 FreeMarker 模板

《如何在SpringBoot中实现FreeMarker模板》FreeMarker是一种功能强大、轻量级的模板引擎,用于在Java应用中生成动态文本输出（如HTML、XML、邮件内容等）,本文... 目录什么是 FreeMarker 模板？在 Spring Boot 中实现 FreeMarker 模板1. 环
阅读更多...
Qt实现网络数据解析的方法总结

Qt实现网络数据解析的方法总结

《Qt实现网络数据解析的方法总结》在Qt中解析网络数据通常涉及接收原始字节流,并将其转换为有意义的应用层数据,这篇文章为大家介绍了详细步骤和示例,感兴趣的小伙伴可以了解下... 目录1. 网络数据接收2. 缓冲区管理（处理粘包/拆包）3. 常见数据格式解析3.1 jsON解析3.2 XML解析3.3 自定义
阅读更多...
SpringMVC 通过ajax 前后端数据交互的实现方法

SpringMVC 通过ajax 前后端数据交互的实现方法

《SpringMVC通过ajax前后端数据交互的实现方法》：本文主要介绍SpringMVC通过ajax前后端数据交互的实现方法,本文给大家介绍的非常详细,对大家的学习或工作具有一定的参考借鉴价... 在前端的开发过程中，经常在html页面通过AJAX进行前后端数据的交互，SpringMVC的controll
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2