多种类型的卷积

2D卷积

       从最原始的图像卷积操作开始。因为图像有单通道图像(灰度图)和多通道图(RGB图)，所以对应常规卷积方式可以分为单通道卷积和多通道卷积。二者本质上并无太大差异，无非对每个通道都要进行卷积而已。先来看单通道卷积。

       在单通道卷积中，针对图像的像素矩阵，卷积操作就是用一个卷积核来逐行逐列的扫描像素矩阵，并与像素矩阵做元素相乘，以此得到新的像素矩阵。其中卷积核也叫过滤器或者滤波器，滤波器在输入像素矩阵上扫过的面积称之为感受野。假设输入图像维度为 n ∗ n ∗ c，滤波器维度为

f ∗ f ∗ 1 ，卷积步长为s，padding大小为p，那么输出维度可以计算为：

    多通道卷积就是每一个通道的卷积核是不一样的，即卷积核的维度将会变为  f ∗ f ∗ c ，之后将每一个通道卷积的结果相加。

       以  n = 5 , c = 3 , f = 3 , s = 1 , p = 0 为例，首先，卷积核的每一通道会与输入图像的每一个通道卷积，得到3个  3 ∗ 3 的卷积结果，之后将这个3个  3 ∗ 3 按相应位置相加，如下所示, RGB三通道的卷积：

 3D卷积就是在2D的基础上加了一个维度.

转置卷积

       转置卷积也叫反卷积,在常规卷积时，我们每次得到的卷积特征图尺寸是越来越小的。但在图像分割等领域，我们是需要逐步恢复输入时的尺寸的。如果把常规卷积时的特征图不断变小叫做下采样，那么通过转置卷积来恢复分辨率的操作可以称作上采样。

       本质上来说，转置卷积跟常规卷积并无区别。不同之处在于先按照一定的比例进行padding来扩大输入尺寸，然后把常规卷积中的卷积核进行转置，再按常规卷积方法进行卷积就是转置卷积。假设输入图像矩阵为X，卷积核矩阵为C，常规卷积的输出为Y，则有：Y=CX .

注意：不是C的转置而是卷积核的转置 ，称之为转置卷积的卷积核. 而且对于同一个卷积核，经过转置卷积操作之后并不能恢复到原始的数值，保留的只有原始的形状，也就是不能通过转置卷积和常规卷积恢复原状.

       这里和直接卷积有很大的区别，直接卷积我们是用一个“小窗户”去看一个“大世界”，而转置卷积是用一个“大窗户”的一部分去看“小世界”。也就是卷积核和像素矩阵大小的区别.

       这里有一点需要注意，我们定义的卷积核是左上角为a，右下角为i，但在可视化转置卷积中，需要将卷积核旋转180°后再进行卷积。由于输入图像太小，我们按照卷积核尺寸来进行补零操作，每边的补零数量显而易见是2，即3-1。这样我们就将一个转置卷积操作转换为对应的直接卷积。如下图：

总结一下将转置卷积转换为直接卷积的步骤：（这里只考虑stride=1，padding=0的情况）
设卷积核大小为k*k，输入为方形矩阵

1. 对输入进行四边补零，单边补零的数量为k-1
2. 将卷积核旋转180°，在新的输入上进行直接卷积

1*1 卷积

1x1卷积在卷积方式上与常规卷积并无差异，主要在于其应用场景和功能

升维降维，实现跨通道的信息整合

       feature map和1*1的卷积核做卷积时，只需要考虑当前像素即可，并不需要考虑周围的像素值。因此第一个作用主要是可以用来调节feature map的通道数，对不同通道上的像素点进行线性组合，即可实现feature map的升维或降维功能，这也是通道见信息的交互和整合过程

深度可分离卷积

       从维度的角度看，卷积核可以看成是一个空间维(宽和高)和通道维的组合，而卷积操作则可以视为空间相关性和通道相关性的联合映射。从1x1卷积来看，卷积中的空间相关性和通道相关性是可以解耦的，将它们分开进行映射，可能会达到更好的效果

       深度可分离卷积是在1x1卷积基础上的一种创新。主要包括两个部分：深度卷积和1x1卷积。深度卷积的目的在于对输入的每一个通道都单独使用一个卷积核对其进行卷积，也就是通道分离后再组合.

假设我们用128个  3 ∗ 3 ∗ 3 的滤波器对一个  7 ∗ 7 ∗ 3 的输入进行卷积，可得到  5 ∗ 5 ∗ 128的输出,其计算量为  5 ∗ 5 ∗ 128 ∗ 3 ∗ 3 ∗ 3 = 86400 .如下图所示：

​

       现在看如何使用深度可分离卷积来实现同样的结果。深度可分离卷积的第一步是深度卷积。这里的深度卷积，就是分别用3个  3 ∗ 3 ∗ 1的滤波器对输入的3个通道分别做卷积，也就是说要做3次卷积，每次卷积都有一个  5 ∗ 5 ∗ 1的输出，组合在一起便是  5 ∗ 5 ∗ 3的输出。

     现在为了拓展深度达到128，我们需要执行深度可分离卷积的第二步：1x1卷积。现在我们用128个  1 ∗ 1 ∗ 3 的滤波器对  5 ∗ 5 ∗ 3进行卷积，就可以得到  5 ∗ 5 ∗ 128的输出。完整过程如下图所示：

​

 相同的卷积计算输出，深度可分离卷积要比常规卷积节省12倍的计算成本。

空洞卷积

        空洞卷积也叫扩张卷积或者膨胀卷积，简单来说就是在卷积核元素之间加入一些空格(零)来扩大卷积核的过程。我们用一个扩展率a来表示卷积核扩张的程度。比如说a=1,2,4的时候卷积核核感受野如下图所示，其中红点表示原卷积核的内容，其他颜色的为扩张的部分：

​

  加入空洞之后的实际卷积核尺寸与原始卷积核尺寸之间的关系：

                                       ​  

       其中k为原始卷积核大小，a为卷积扩展率，K为经过扩展后实际卷积核大小。除此之外，空洞卷积的卷积方式跟常规卷积一样。a=2时的空洞卷积的动态示意图如下所示：

                 ​

       那么空洞卷积有什么好处呢？一个直接作用就是可以扩大卷积感受野，空洞卷积几乎可以在零成本的情况下就可以获取更大的感受野来扩充更多信息，这有助于在检测和分割任务中提高准确率。空洞卷积的另一个优点则是可以捕捉多尺度的上下文信息，当我们使用不同的扩展率来进行卷积核叠加时，获取的感受野就丰富多样。

       但是，空洞卷积也有缺点，

局部信息丢失：由于空洞卷积的计算方式类似于棋盘格式，某一层得到的卷积结果，来自上一层的独立的集合，没有相互依赖，因此该层的卷积结果之间没有相关性，即局部信息丢失。
远距离获取的信息没有相关性：由于空洞卷积稀疏的采样输入信号，使得远距离卷积得到的信息之间没有相关性，影响分类结果

解决办法-混合空洞卷积

       对于上个 section 里提到的几个问题，图森组的文章对其提出了较好的解决的方法。他们设计了一个称之为 HDC 的设计结构。
HDC原则 (Hybrid Dilated Convolution) - 图森组
       混合空洞卷积，在每一层使用不同的rate，把dilatioin rate 变成锯齿形式的也就是不同层之间的dilation不断变化。目标是最后的接收野全覆盖整个区域。

1.叠加卷积的 dilation rate 不能有大于1的公约数。比如 [2, 4, 6] 则不是一个好的三层卷，有些点永远不会被考虑。
2.将 dilation rate 设计成锯齿状结构。例如[1, 2, 3, 1, 2, 3] 循环结构，覆盖了所有点。
3.需要满足一下这个式子，M<=K：

        dilation rate是空洞卷积率，记为 ri，就是扩张倍数；K是卷积核尺寸
举例：对于常见的扩张卷积核大小K=3，如果r=[1,2,5] 则

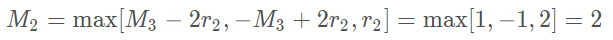
 此时M2=2 ≤ K=3 满足设计要求，设计的示意图如下：

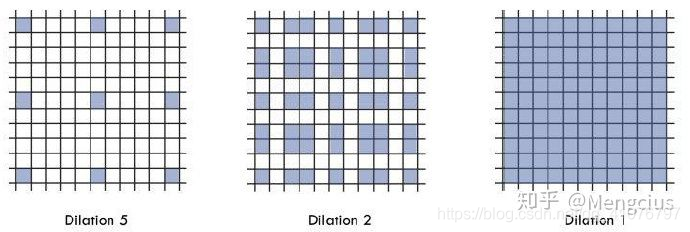
       上图解释一下，从左往右看，也就是从顶部往下部看，顶部进行size=5的空洞卷积，所用到的蓝点是根据r=2的空洞卷积卷过来的，还原回去就是中间的图，可以看到还是有一些方块是白色的，也就是没有参与运算的，别急，再看这些蓝方块是根据r=1的方块填充的，然后还原，得到最右图，可见所有的输入元素都被参与运算了，使得卷积后的某个像素考虑了感受野内所有的输入像素点，这样就不存在局部信息不完整以及输入像素点之间相关性不强等问题了。