如何使用图卷积网络对图进行深度学习

简介

由于高度复杂但信息丰富的图结构，图上的机器学习是一项艰巨的任务。这篇文章是关于如何使用图卷积网络 (GCN) 对图进行深度学习的系列文章中的第一篇，GCN 是一种强大的神经网络，旨在直接处理图并利用其结构信息。

在这篇文章中，我会给出一个1.产品我到GCNs和说明如何信息是通过使用编码示例的GCN的隐藏层传播。我们将看到 GCN 如何聚合来自前几层的信息，以及这种机制如何生成图中节点的有用特征表示。

什么是图卷积网络？

GCN 是一种非常强大的神经网络架构，用于图上的机器学习。事实上，它们是如此强大，以至于即使是随机启动的 2 层 GCN也可以产生网络中节点的有用特征表示。下图说明了由这种 GCN 生成的网络中每个节点的二维表示。请注意，即使没有任何训练，网络中节点的相对接近度也保留在二维表示中。

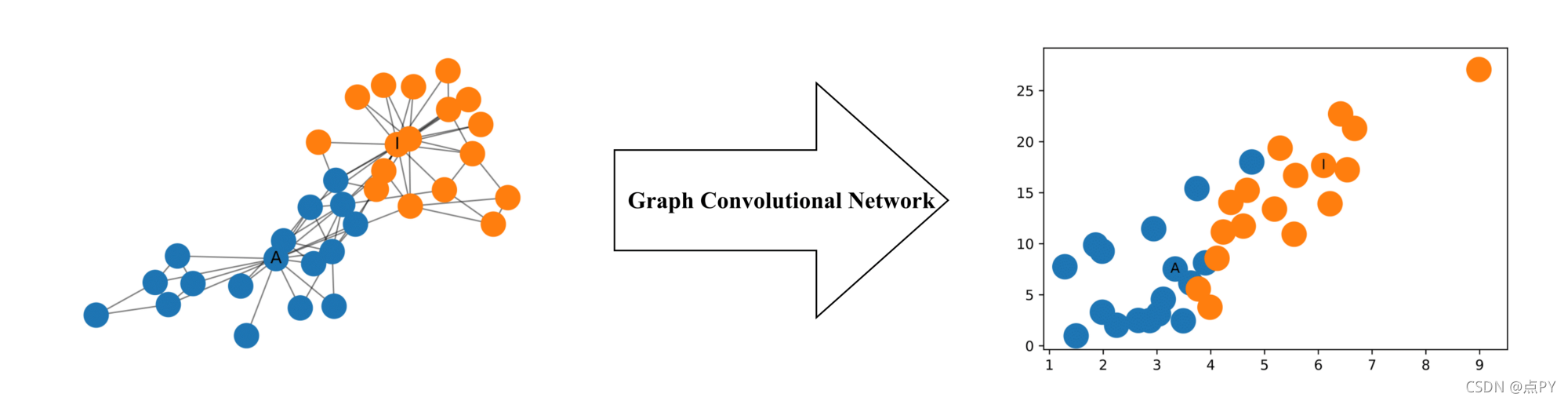
更正式地说，图卷积网络 (GCN)是一种对图进行操作的神经网络。给定一个图G = (V, E)，一个 GCN 作为输入

• 一个输入特征矩阵N × F⁰特征矩阵，X，其中N是节点的数量，F⁰是每个节点的输入特征的数量，并且

• 图结构的N × N矩阵表示，例如G.[1]的邻接矩阵A

因此，GCN 中的隐藏层可以写为Hⁱ = f( H ⁱ⁻¹, A ))，其中H ⁰ = X并且f是 传播 [1]。每层Hⁱ对应一个N × F ⁱ特征矩阵，其中每一行是一个节点的特征表示。在每一层，使用传播规则f聚合这些特征以形成下一层的特征。通过这种方式，每个连续层的特征变得越来越抽象。在这个框架中，GCN 的变体仅在传播规则f [1]的选择上有所不同。

一个简单的传播规则

最简单的传播规则之一是 [1]：

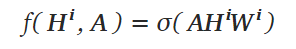
其中Wⁱ是第i层的权重矩阵，σ是非线性激活函数，例如ReLU 函数。权重矩阵的维度为F ⁱ × Fⁱ ⁺ ¹；换句话说，权重矩阵的第二维的大小决定了下一层的特征数量。如果您熟悉卷积神经网络，此操作类似于过滤操作，因为这些权重在图中的节点之间共享。

简化

让我们在最简单的级别上检查传播规则。让

• i = 1 , st f是输入特征矩阵的函数，
• σ是恒等函数，并且
• 选择权重 st AH ⁰ W ⁰ = AXW ⁰ = AX。

换句话说，f( X , A ) = AX。这个传播规则可能有点太简单了，但我们稍后会添加缺失的部分。作为旁注，AX现在相当于多层感知器的输入层。

一个简单的图形示例

作为一个简单的例子，我们将使用下图：

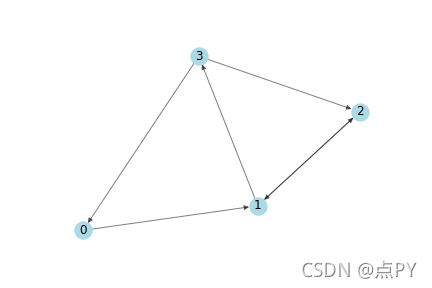
下面是它的numpy邻接矩阵表示。

A = np.matrix([[0, 1, 0, 0],[0, 0, 1, 1], [0, 1, 0, 0],[1, 0, 1, 0]],dtype=float
)

接下来，我们需要特征！我们根据每个节点的索引为每个节点生成 2 个整数特征。这使得稍后手动确认矩阵计算变得容易。

In [3]: X = np.matrix([[i, -i]for i in range(A.shape[0])], dtype=float)X
Out[3]: matrix([[ 0.,  0.],[ 1., -1.],[ 2., -2.],[ 3., -3.]])

应用传播规则

好吧！我们现在有一个图，它的邻接矩阵A和一组输入特征X。让我们看看当我们应用传播规则时会发生什么：

In [6]: A * X 
Out[6]: matrix([ [ 1., -1.], [ 5., -5.], [ 1., -1.], [ 2., -2. ]]

发生了什么？ 每个节点（每一行）的表示现在是其邻居特征的总和！换句话说，图卷积层将每个节点表示为其邻域的聚合。我鼓励你自己检查计算。请注意，在这种情况下，如果存在从v到n的边，则节点n是节点v的邻居。

存在的问题

您可能已经发现了问题：

• 节点的聚合表示不包括其自身的特征！该表示是邻居节点特征的聚合，因此只有具有自循环的节点才会在聚合中包含自己的特征。
• 度数大的节点在其特征表示中将具有较大的值，而度数较小的节点将具有较小的值。这可能会导致梯度消失或爆炸 [1, 2]，但对于通常用于训练此类网络并对每个输入特征的尺度（或值范围）敏感的随机梯度下降算法也存在问题。

在下文中，我将分别讨论这些问题中的每一个。

添加自循环

为了解决第一个问题，可以简单地为每个节点添加一个自循环 [1, 2]。实际上，这是通过在应用传播规则之前将单位矩阵添加I到邻接矩阵A来完成的。

In [4]: I = np.matrix(np.eye(A.shape[0]))I
Out[4]: matrix([[1., 0., 0., 0.],[0., 1., 0., 0.],[0., 0., 1., 0.],[0., 0., 0., 1.]])
In [8]: A_hat = A + IA_hat * X
Out[8]: matrix([[ 1., -1.],[ 6., -6.],[ 3., -3.],[ 5., -5.]])

由于该节点现在是自己的邻居，所以在总结其邻居的特征时，包括该节点自己的特征！

规范化特征表示

通过将邻接矩阵A乘以逆度矩阵D[1]，可以通过节点度对特征表示进行归一化。因此，我们简化的传播规则如下所示 [1]：

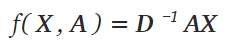
让我们看看发生了什么。我们首先计算度矩阵。

In [9]: D = np.array(np.sum(A,axis=0))[0] D = np.matrix(np.diag(D)) D 
Out[9]: matrix([ [1. , 0., 0., 0.], [0., 2., 0., 0.], [0., 0., 2., 0.], [0., 0., 0., 1 .] ])

在应用规则之前，让我们看看变换后的邻接矩阵会发生什么。

前

A = np.matrix([ [0, 1, 0, 0], [0, 0, 1, 1], [0, 1, 0, 0], [1, 0, 1, 0]], dtype=float
）

后

In [10]: D**-1 * A 
Out[10]: matrix([ [ [0. , 1. , 0. , 0. ], [0. , 0. , 0.5, 0.5], [0. , 0.5, 0. , 0. ], [0.5, 0. , 0.5, 0. ] 
])

观察到邻接矩阵每一行的权重（值）已经除以该行对应的节点的度数。我们将传播规则与变换后的邻接矩阵一起应用

In [11]: D**-1 * A * X 
Out[11]: matrix([ [ [ 1. , -1. ], [ 2.5, -2.5], [ 0.5, -0.5], [ 2. , - 2.] ])

并得到与相邻节点特征的均值相对应的节点表示。这是因为（转换后的）邻接矩阵中的权重对应于相邻节点特征的加权总和中的权重。我再次鼓励您亲自验证这一观察结果。

把它放在一起

我们现在结合自循环和归一化技巧。此外，我们将重新引入我们之前丢弃的权重和激活函数，以简化讨论。

加回权重

首要任务是应用权重。注意这里D_hat是 的度矩阵A_hat = A + I，即A强制自环的度矩阵。

In [45]: W = np.matrix([[1, -1],[-1, 1]])D_hat**-1 * A_hat * X * W
Out[45]: matrix([[ 1., -1.],[ 4., -4.],[ 2., -2.],[ 5., -5.]])

如果我们想减少输出特征表示的维度，我们可以减少权重矩阵的大小W：

In [46]: W = np.matrix([[1],[-1]])D_hat**-1 * A_hat * X * W
Out[46]: matrix([[1.],[4.],[2.],[5.]]
)

添加激活函数

我们选择保留特征表示的维度并应用ReLU激活函数。

In [51]: W = np.matrix([ [1, -1], [-1, 1] ]) relu(D_hat**-1 * A_hat * X * W) 
Out[51]: matrix([[ 1., 0.], [4., 0.], [2., 0.], [5., 0.]])

瞧！一个带有邻接矩阵、输入特征、权重和激活函数的完整隐藏层！

回到现实

现在，我们终于可以在真实图上应用图卷积网络了。我将向您展示如何生成我们在文章早期看到的特征表示。

扎卡里的空手道俱乐部

Zachary 的空手道俱乐部是一个常用的社交网络，其中节点代表空手道俱乐部的成员，边缘代表他们之间的相互关系。在 Zachary 学习空手道俱乐部时，管理员和教练之间发生了冲突，导致俱乐部一分为二。下图显示了网络的图形表示，节点根据俱乐部的哪个部分进行标记。管理员和讲师分别标有“A”和“I”。

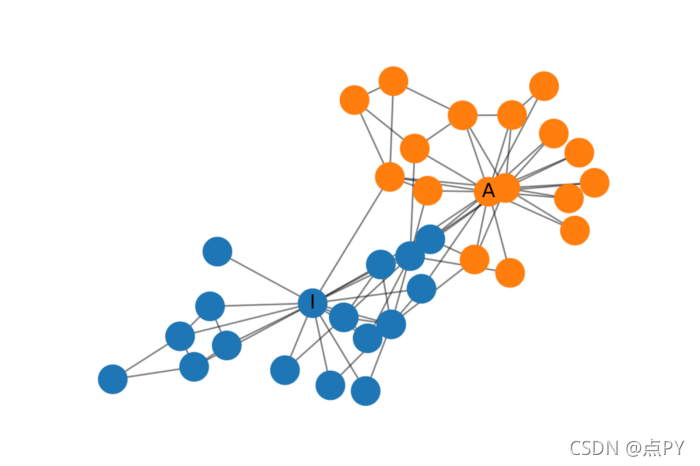
构建 GCN

现在让我们构建图卷积网络。我们实际上不会训练网络，而是简单地随机初始化它以产生我们在本文开头看到的特征表示。我们将使用networkx它具有易于获得的俱乐部图形表示，并计算A_hat和D_hat矩阵。

from networkx import karate_club_graph, to_numpy_matrix
zkc = karate_club_graph()
order = sorted(list(zkc.nodes()))
A = to_numpy_matrix(zkc, nodelist=order)
I = np.eye(zkc.number_of_nodes())
A_hat = A + I
D_hat = np.array(np.sum(A_hat, axis=0))[0]
D_hat = np.matrix(np.diag(D_hat))

接下来，我们将随机初始化权重。

W_1 = np.random.normal( loc=0, scale=1, size=(zkc.number_of_nodes(), 4)) 
W_2 = np.random.normal( loc=0, size=(W_1.shape[1], 2))

堆叠 GCN 层。我们在这里仅使用单位矩阵作为特征表示，即每个节点都表示为一个单热编码的分类变量。

def gcn_layer(A_hat, D_hat, X, W):return relu(D_hat**-1 * A_hat * X * W)
H_1 = gcn_layer(A_hat, D_hat, I, W_1)
H_2 = gcn_layer(A_hat, D_hat, H_1, W_2)
output = H_2

我们提取特征表示。

feature_representations = {node: np.array(output)[node] for node in zkc.nodes()}

瞧！将 Zachary 的空手道俱乐部中的社区很好地分开的特征表示。而且我们还没有开始训练呢！

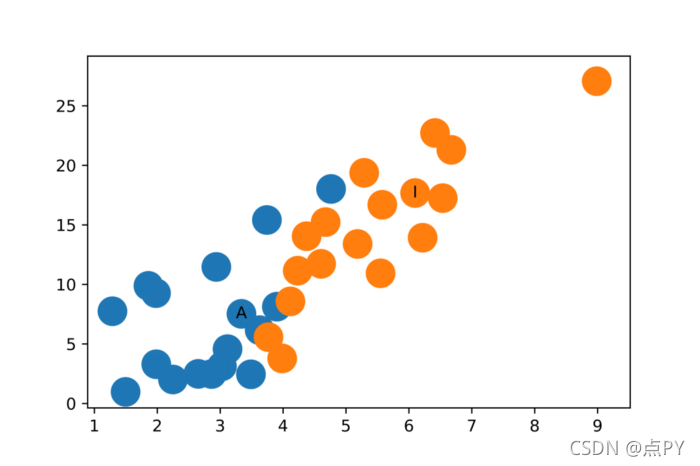
Zachary 的空手道俱乐部中节点的特征表示

我应该注意到，对于这个例子，随机初始化的权重很可能在 x 轴或 y 轴上给出 0 值作为 ReLU 函数的结果，因此需要一些随机初始化来生成上图。

结论

在这篇文章中，我对图卷积网络进行了高级介绍，并说明了 GCN 中每一层节点的特征表示如何基于其邻域的聚合。我们看到了如何使用 numpy 构建这些网络以及它们有多么强大：即使是随机初始化的 GCN 也可以将 Zachary 的空手道俱乐部中的社区分开。

参考
https://towardsdatascience.com/how-to-do-deep-learning-on-graphs-with-graph-convolutional-networks-7d2250723780