ACM基础：贪心之背包问题knapsack

本文主要是介绍ACM基础：贪心之背包问题knapsack，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

一、背包问题

1.描述

小偷抢劫商店，发现n件物品，物品i价值$v_i$美元，重量为$w_i$磅，小偷在背包中最多只能携带W磅重量，但他想尽可能多地携带贵重物品。他应该带哪些物品？

问题符号：

• n：物品的个数
• i：物品的序号
• $v_i$：某物品的价值value
• $w_i$：某物品的重量weight
• W：背包的最大承重量

解法符号：

• $x_i$：表示该物品装入背包多少。在0-1背包问题中，0（不拿）或1（拿走整件）；在分数背包问题中，是个浮点数$[0.0,1.0]$，0.0（不拿）或0.x（拿走部分）或1.0（拿走整件）

解法：
在满足$\sum _{1\le i\le n}{w}_i\ast x_i\le W$的条件下，使$\sum _{1\le i\le n}{v}_i\ast x_i$最大。

2.难度划分

依据$x_i$是分数还是01，命名：

• 简单：分数背包问题(Fractional knapsack)
• 难：0-1背包问题(0-1 knapsack)

二、简单：分数背包问题(Fractional knapsack)

1.思路

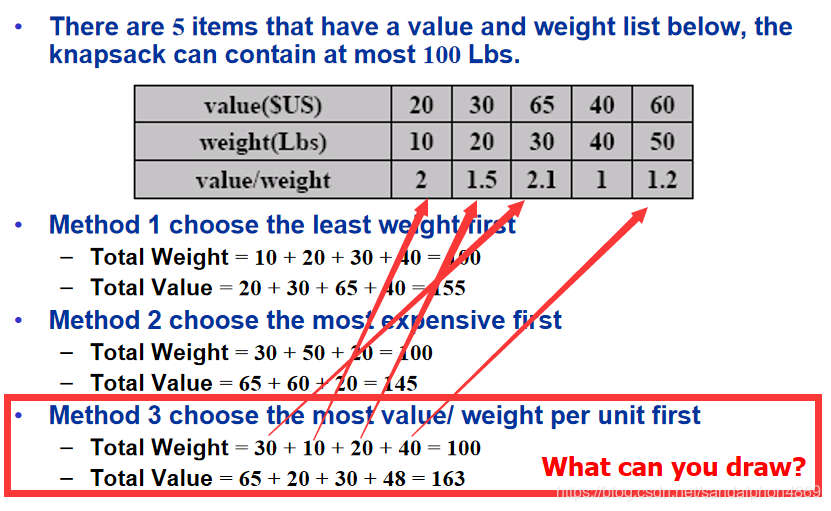
因为可以拿走物品的部分，所以不妨将所有物品打碎当成单位物品来看，我们只需要拿走性价比（价值vi/重量wi）最高的单位物品就行，依照性价比降序来拼凑重量够整个背包。

2.伪代码

// v是vi数组，每个物品的价值
// w是wi数组，每个物品的重量
// W是背包的最大负重
// x是xi数组，每个物品装入背包的多少
// n是物品的数量
// 注意：对v数组和w数组有要求，按照性价比降序排列物品，即v(i)/w(i) ≥ v(i+1)/w(i+1)
GREADY-KNAPSACK(v, w, W, x, n)// 初始化都为0，哪个都不装入x ← 0// 背包的剩余容量，开始什么都不装c ← W// 遍历每个物品for i ← 1 to n// 如果物品的重量小于等于背包剩余容量，则可装入do	if w(i) ≤ c// 装入整件物品then	x(i) ← 1// 背包剩余容量变少c ← c - w(i)// 如果装不进去，那么退出for循环else	exit// i ≤ n表示exit退出for循环（注意：for成功遍历完每个物品后，i++的最后结果是i=n+1）// 如果i ≤ n，说明两种情况，一种是整件物品装不进去但可以装进部分，另一种是背包剩余空间用尽了if i ≤ n// 装入该物品的部分：剩余空间/物品总重// 第二种情况进入没事，因为c = 0 时,x(i) = 0// 不存在c>=w(i)的情况，要不然就不会exit退出for循环then	x(i) ← c/w(i)return x

3.c++实现

#include <iostream>
#include <string.h>
using namespace std;// 物品的个数
#define n 5// 调整为性价比降序
void costPerformance_insertSort(double v[n], double w[n])
{// int c[n] = {};// for(int i = 1;i<n;i++)// 遍历第二个到最后一个，为A[i]，表示要插入排序好部分的元素。// 因为第一个不用比较，所以从第二个开始for (int i = 1; i < n; i++){// 当前待插入的元素double key_v = v[i];double key_w = w[i];// 将A[i]插入到已经排序好的部分，就是A[i]前面的部分A[1...i-1]// 倒着看前面的，确定要插入的位置int j = i - 1;// 在不越界时，并且因为是降序所以是当前一个元素更小时继续while (j >= 0 && v[j] / w[j] < key_v / key_w){// 前一个元素后移v[j + 1] = v[j];w[j + 1] = w[j];// 再往前面一个j--;}// 此时才正式插入元素// 因为退出while循环时是A[j]>=key，所以插入到A[j]后面A[j+1]v[j + 1] = key_v;w[j + 1] = key_w;}
}void gready_fractional_knapsack(double v[n], double w[n], double W, double x[n])
{// 初始化都为0，哪个都不装入memset(x, 0, sizeof(x));// 背包的剩余容量，开始什么都不装double c = W;// 遍历每个物品int i;for (i = 0; i < n; i++){// 如果物品的重量小于等于背包剩余容量，则可装入if (w[i] <= c){// 装入整件物品x[i] = 1;// 背包剩余容量变少c -= w[i];}// 如果装不进去，那么退出for循环else{break;}}// i ≤ n表示exit退出for循环（注意：for成功遍历完每个物品后，i++的最后结果是i=n+1）// 如果i ≤ n，说明两种情况，一种是整件物品装不进去但可以装进部分，另一种是背包剩余空间用尽了if (i <= n){// 装入该物品的部分：剩余空间/物品总重// 第二种情况进入没事，因为c = 0 时,x(i) = 0// 不存在c>=w(i)的情况，要不然就不会exit退出for循环x[i] = c / w[i];}
}
int main()
{// 因为算性价比是小数，用double方便// 某物品的价值valuedouble v[n] = {20, 30, 65, 40, 60};// 某物品的重量weightdouble w[n] = {10, 20, 30, 40, 50};// 背包的最大承重量double W = 100;// 该物品装入背包多少double x[n] = {};// 调整为性价比降序costPerformance_insertSort(v, w);// 背包算法gready_fractional_knapsack(v, w, W, x);// 总重double my_weight = 0;// 总价值double my_value = 0;// 输出for (int i = 0; i < n; i++){my_weight += w[i] * x[i];my_value += v[i] * x[i];cout << x[i] << " ";}cout << endl;printf("[my_weight]%lf\n", my_weight);printf("[my_value]%lf\n", my_value);return 0;
}

三、难：0-1背包问题(0-1 knapsack)

咕咕咕

import java.util.*;public class Knapsack {class Commodity implements Comparable{int num;int values;int weight;public Commodity(int num, int values, int weight){this.values = values;this.weight = weight;this.num = num;}@Overridepublic int compareTo(Object o) {  //����double vdw1 = (double)this.values/this.weight;double vdw2 = (double)((Commodity)o).values/((Commodity)o).weight;if(vdw1 > vdw2) return -1;else if(vdw1 == vdw2) return 0;else return  1;}}public static void one_zero_knapsack(Commodity[] commodities, int bag, boolean[] x){int n = commodities.length;boolean[][] memory = new boolean[commodities.length+1][bag+1];int[][] c = new int[commodities.length+1][bag+1];caculate_c(commodities, c, memory, x, commodities.length,bag);}static void caculate_c(Commodity[] commodities, int[][] c, boolean[][] memory, boolean[] x, int i, int bag){if(i == 0 || bag ==0) {c[i][bag] = 0;memory[i][bag] = true;}else if(commodities[i-1].weight > bag) {if(!memory[i-1][bag]){caculate_c(commodities, c, memory, x, i-1, bag);}	c[i][bag] = c[i-1][bag];memory[i][bag] = true;}else if(i>0 && bag>=commodities[i-1].weight){if(!memory[i-1][bag-commodities[i-1].weight]){caculate_c(commodities, c, memory, x, i-1, bag-commodities[i-1].weight);}if(!memory[i-1][bag]){caculate_c(commodities, c, memory, x, i-1, bag);}int value1 = c[i-1][bag-commodities[i-1].weight] + commodities[i-1].values;int value2 = c[i-1][bag];if(value1 > value2){x[commodities[i-1].num] = true;c[i][bag] = value1;memory[i][bag] = true;}  else {c[i][bag] = value2;memory[i][bag] = true;}}}public static void fractional_knapsack(Commodity[] commodities, int bag, double[] x){Arrays.sort(commodities);int n = commodities.length;for(int i=0; i<n; ++i){if(bag - commodities[i].weight >= 0) {bag -= commodities[i].weight;x[commodities[i].num] = 1;}else{x[commodities[i].num] = (double)bag/commodities[i].weight;break;}}}/*** @param args*/public static void main(String[] args) {Knapsack ks = new Knapsack();Commodity[] commodities = {ks.new Commodity(0,20,10),ks.new Commodity(1,30,20),ks.new Commodity(2,65,30),ks.new Commodity(3,40,40),ks.new Commodity(4,60,50)};//Arrays.sort(commodities);int bag = 100;//0-1 knapsackboolean[] one_zero = new boolean[commodities.length];for(int i=0; i<commodities.length; ++i){one_zero[i] = false;}Knapsack.one_zero_knapsack(commodities, bag, one_zero);System.out.println("0-1 knapsack:");for(int i=0; i<commodities.length; ++i){System.out.println(one_zero[i]);}//fractional knapsack	double[] fra  = new double[commodities.length];Knapsack.fractional_knapsack(commodities, bag, fra);System.out.println("fractional knapsack:");for(int i=0; i<commodities.length; ++i){System.out.println(fra[i]);}}}

这篇关于ACM基础：贪心之背包问题knapsack的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---