不仅适用于方阵的回形矩阵

本文主要是介绍不仅适用于方阵的回形矩阵，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

分析

基本情况

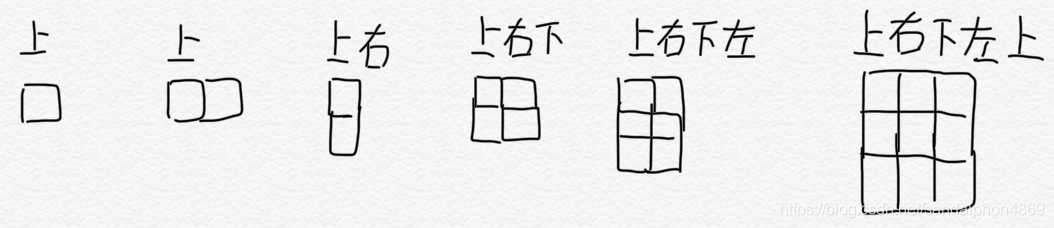
这就是全部的基本情况，之后所有都是在此基础上的变形。

遍历方式

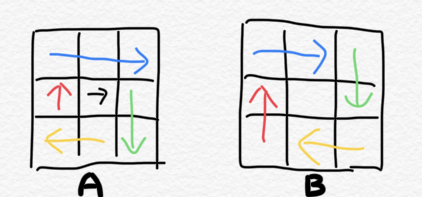
对应：for (int i = p; i <= n - 1 - p; i++)中是<=（A）还是<（B）
我们采用A方式，而不采用B方式。因为B方式无法处理只有一个时的情况。

跳出条件

• 设立了两个跳出判断。
• while的跳出是①、④、⑤、⑥
• if的跳出是②、③

答案

vector<vector<int>> matrix(6, vector<int>(4, 0));
int m = matrix.size();    // 行
int n = matrix[0].size(); // 列
int count = 0, max_count = m * n;
int p = 0;
while (count < max_count)
{for (int i = p; i <= n - 1 - p; i++) // 上{matrix[p][i] = ++count;}for (int i = p + 1; i <= m - 1 - p; i++) // 右{matrix[i][n - 1 - p] = ++count;}if (count >= max_count){break;}for (int i = n - 2 - p; i >= p; i--) // 下{matrix[m - 1 - p][i] = ++count;}for (int i = m - 2 - p; i > p; i--) // 左{matrix[i][p] = ++count;}p++;
}for (int i = 0; i < m; i++)
{for (int j = 0; j < n; j++)printf("%2d ", matrix[i][j]);printf("\n");
}

这篇关于不仅适用于方阵的回形矩阵的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---