【SBL】稀疏贝叶斯学习模型Sparse Bayesian Learning

理论学习

稀疏贝叶斯学习是由Tipping提出，并作为使用内核的机器学习方法，基于其优秀的分类和回归能力，SBL被广泛应用到很多研究领域。
进一步，不含有内核的SBL也被证明在稀疏信号恢复，稀疏表示和压缩感知方面具有优秀的结果。
在很多情况下，信号恢复可被认为是回归，因为它们的目标是最小泛化误差，因此，我们在做研究的时候，对影响因素X采用不含内核的SBL模型
稀疏信号恢复公式


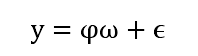
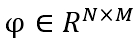
表示N个样本的矩阵，并且每个样本皆有M个特征

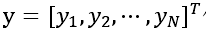
代表目标变量

$ϵ$ 表示白噪声

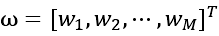
代表模型学习用来构成$\phi$中的每一列的权重

SBL模型的目标
是寻找一个一个包含很多零值的$\omega$权重向量，同时结果很准确的逼近目标向量Y
在SBL模型中，高斯似然函数模型可表示为：

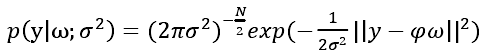
在这种情况下，获取$\omega$的最大似然估计的任务等价于在第一个式子中寻找最小2范数解。然后这种解同时常识非稀疏的。
因此为了找到稀疏解，SBL从数据中估计参数化的先验权重，过程可以用如下公式表达：


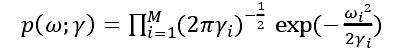
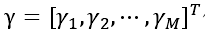
表示M个超参数向量，它控制每一个权重的先验方差，从数据中估计这些超参数的过程分解为两个步骤

• 将权重边缘化
• 通过最大似然优化算法

借用Wipf的研究
SBL的优势

1.其他贝叶斯学习算法需要满足第一个式子中的$\phi$矩阵中M远大于N，而SBL在M<N时，可以获得良好的结果
2.SBL模型只需设置很少量的参数，因此没有必要优化其中的参数，这大大提高了模型训练的效率，结果也更加可靠稳定【鲁棒性】
3.SBL模型估计出的权重可以衡量一个特征在回归上的重要性，有点像回归估计中参数的显著性，提高每个特征的可解释性

鉴于SBL优秀的回归能力，以及衡量每个特征对于回归结果的贡献度，我们通常用SBL模型来分析某个Y的影响因素X，

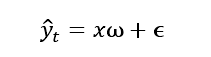
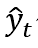
代表t时期y的预测值

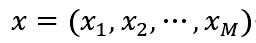
影响因素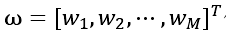
每个影响因素的权重